高一数学2.1.4 指数函数的性质及其应用.ppt
文档属性
| 名称 | 高一数学2.1.4 指数函数的性质及其应用.ppt |  | |
| 格式 | zip | ||
| 文件大小 | 377.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-26 17:08:58 | ||
图片预览








文档简介
课件25张PPT。2.1.4 指数函数的性质及其应用【学习目标】
1.熟练掌握指数函数图象和性质.
2.掌握指数型函数的定义域、值域,会判断其单调性.
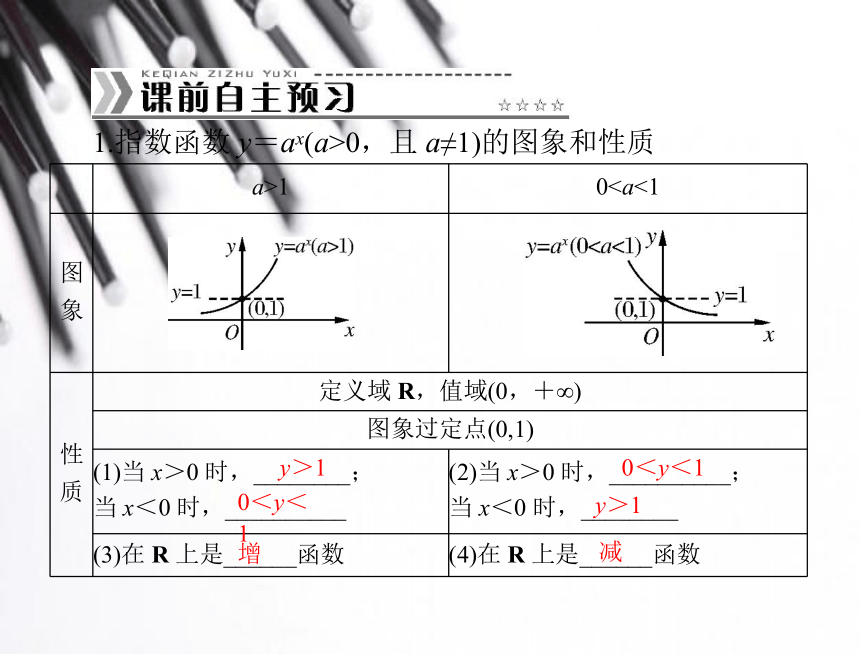
3.培养数学应用意识.1.指数函数 y=ax(a>0,且 a≠1)的图象和性质y>10<y<10<y<1y>1增减 2.(1)若 a>b>1,当 x>0 时,函数 y=ax 图象在函数 y=bx
图象的________方;当 x<0 时,函数 y=ax 图象在函数 y=bx图象的________方.上下上下 (2)若 1>a>b>0,当 x>0 时,函数 y=ax 图象在函数 y=
bx 图象的________方;当 x<0 时,函数 y=ax 图象在函数 y=
bx 图象的________方.练习1:不等式2x>21-x的解集为_______________.
A.{-1,1}
C.{0}
B.{-1}
D.{-1,0}练习 3:函数 y=7-x 与函数____________的图象关于 y 轴对称.y=7xB则M∩N=( ) 【问题探究】答案:图略,关于y轴对称.题型 1 利用指数函数的单调性比较大小
【例 1】 比较下列各组数的大小: 在进行数的大小比较时,①若底数相同,则可
根据指数函数的增减性得出结果;②若底数不相同,则首先考
虑把它们化成同底数;不能化成同底数时,就考虑引进第三个
数(0,1 等)分别与之比较,从而得出结果.【变式与拓展】f(n),则 m,n 的大小关系为________.m<n>f(n),得 m<n.题型 2 指数函数的最值问题思维突破:结合函数的单调性,对 a 进行分类讨论. (1)指数函数y=ax(a>1)为增函数,在闭区间[s,t]上存在最大、最小值.当x=s时,函数有最小值as;当x=t时,函数有最大值at.
(2)指数函数y=ax(0<a<1)为减函数,在闭区间[s,t]上存在最大、最小值.当x=s时,函数有最大值as;当x=t时,函数有最小值at. 【变式与拓展】a=________.题型 3 指数函数性质的综合应用(1)求 f(x)的定义域;
(2)求 f(x)的值域;
(3)判断函数 f(x)的奇偶性;
(4)证明 f(x)在(-∞,+∞)上是增函数. 对函数奇偶性与单调性的判别,都是直接利用
它们的定义来解决.需要我们理解这两个定义,掌握其运用的基
本模式,并能熟练的进行代数变形.【变式与拓展】CA.(0,+∞)
C.(0,1) B.(-∞,1)
D.(1,+∞)=()A.{y|y>1}B.{y|y≥1}C.{y|y>0}D.{y|y≥0} 易错分析:对于集合问题,要首先确定集合的元素是什么
(数集、点集或某类图形),然后确定处理此类问题的方法.本题
集,错选 A 或 B.实际上,两集合的元素是 y,是求两函数的值
域的交集.答案:C[方法·规律·小结]指数函数 y=ax(a>0,a≠1)的性质.(1)当底数 a 大小不定时,必须分“a>1”和“0<a<1”两种情况讨论.(2)当 0<a<1 时,x→+∞,y→0;
当 a>1 时,x→-∞,y→0.当 a>1 时,a 的值越大,图象越靠近 y 轴,递增的速度越快; 当 0<a<1 时,a 的值越小,图象越靠近 y 轴,递减的速
度越快(其中“x→+∞”的意义是“x 接近于正无穷大”). (3)指数函数在同一直角坐标系中的图象的相对位置与底
数大小的关系的判断方法:作直线 x=1,与图象的交点的纵坐
标,即为指数函数的底数值(如图 2-1-2).图 2-1-2
1.熟练掌握指数函数图象和性质.
2.掌握指数型函数的定义域、值域,会判断其单调性.
3.培养数学应用意识.1.指数函数 y=ax(a>0,且 a≠1)的图象和性质y>10<y<10<y<1y>1增减 2.(1)若 a>b>1,当 x>0 时,函数 y=ax 图象在函数 y=bx
图象的________方;当 x<0 时,函数 y=ax 图象在函数 y=bx图象的________方.上下上下 (2)若 1>a>b>0,当 x>0 时,函数 y=ax 图象在函数 y=
bx 图象的________方;当 x<0 时,函数 y=ax 图象在函数 y=
bx 图象的________方.练习1:不等式2x>21-x的解集为_______________.
A.{-1,1}
C.{0}
B.{-1}
D.{-1,0}练习 3:函数 y=7-x 与函数____________的图象关于 y 轴对称.y=7xB则M∩N=( ) 【问题探究】答案:图略,关于y轴对称.题型 1 利用指数函数的单调性比较大小
【例 1】 比较下列各组数的大小: 在进行数的大小比较时,①若底数相同,则可
根据指数函数的增减性得出结果;②若底数不相同,则首先考
虑把它们化成同底数;不能化成同底数时,就考虑引进第三个
数(0,1 等)分别与之比较,从而得出结果.【变式与拓展】f(n),则 m,n 的大小关系为________.m<n>f(n),得 m<n.题型 2 指数函数的最值问题思维突破:结合函数的单调性,对 a 进行分类讨论. (1)指数函数y=ax(a>1)为增函数,在闭区间[s,t]上存在最大、最小值.当x=s时,函数有最小值as;当x=t时,函数有最大值at.
(2)指数函数y=ax(0<a<1)为减函数,在闭区间[s,t]上存在最大、最小值.当x=s时,函数有最大值as;当x=t时,函数有最小值at. 【变式与拓展】a=________.题型 3 指数函数性质的综合应用(1)求 f(x)的定义域;
(2)求 f(x)的值域;
(3)判断函数 f(x)的奇偶性;
(4)证明 f(x)在(-∞,+∞)上是增函数. 对函数奇偶性与单调性的判别,都是直接利用
它们的定义来解决.需要我们理解这两个定义,掌握其运用的基
本模式,并能熟练的进行代数变形.【变式与拓展】CA.(0,+∞)
C.(0,1) B.(-∞,1)
D.(1,+∞)=()A.{y|y>1}B.{y|y≥1}C.{y|y>0}D.{y|y≥0} 易错分析:对于集合问题,要首先确定集合的元素是什么
(数集、点集或某类图形),然后确定处理此类问题的方法.本题
集,错选 A 或 B.实际上,两集合的元素是 y,是求两函数的值
域的交集.答案:C[方法·规律·小结]指数函数 y=ax(a>0,a≠1)的性质.(1)当底数 a 大小不定时,必须分“a>1”和“0<a<1”两种情况讨论.(2)当 0<a<1 时,x→+∞,y→0;
当 a>1 时,x→-∞,y→0.当 a>1 时,a 的值越大,图象越靠近 y 轴,递增的速度越快; 当 0<a<1 时,a 的值越小,图象越靠近 y 轴,递减的速
度越快(其中“x→+∞”的意义是“x 接近于正无穷大”). (3)指数函数在同一直角坐标系中的图象的相对位置与底
数大小的关系的判断方法:作直线 x=1,与图象的交点的纵坐
标,即为指数函数的底数值(如图 2-1-2).图 2-1-2
