2.2.3对数函数及其性质(1).ppt
文档属性
| 名称 | 2.2.3对数函数及其性质(1).ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 364.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-26 00:00:00 | ||
图片预览








文档简介
课件29张PPT。2.2.3对数函数及其性质(1)【学习目标】 1.通过具体实例,直观了解对数函数模型所刻画的数量关
系,初步理解对数函数的概念,体会对数函数是一类重要的函
数模型.2.能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点. 1.对数函数
一般地,我们把函数 y=logax(a>0,且 a≠1)叫做对数函数,
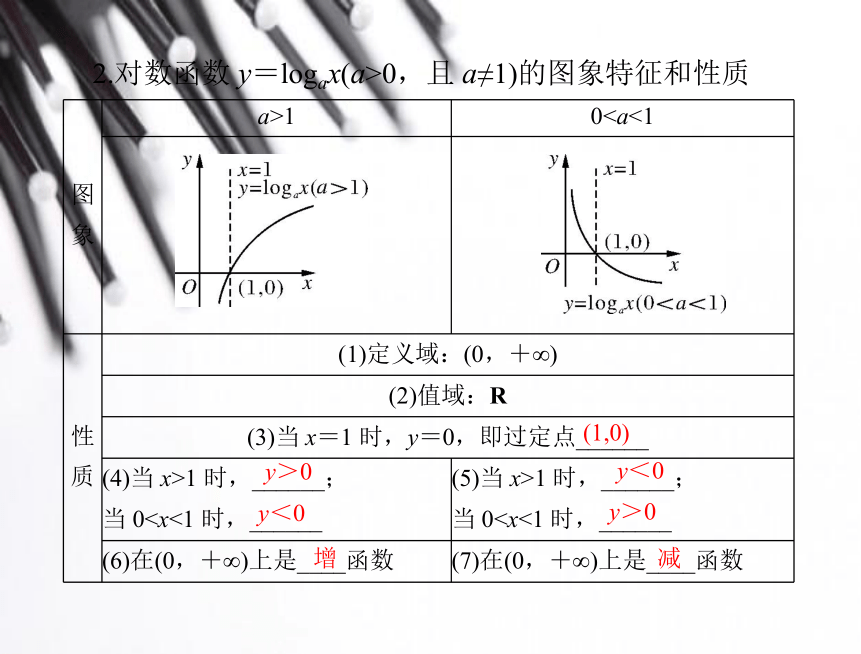
其中________是自变量,函数的定义域是___________,值域是实数集 R.x(0,+∞)2.对数函数 y=logax(a>0,且 a≠1)的图象特征和性质(1,0)y>0y<0y<0y>0增减(续表)y1<y2y1>y2练习2:函数f(x)=log(a-1)x在(0,+∞)上单调递减,则实数 a 的取值范围为__________.11.比较下列两组数的大小:
(1)log108与log1015; (2)log0.50.9与log0.50.6.
答案:(1)log1015>log108;(2)log0.50.6>log0.50.9. 2.求下列函数的定义域:题型 1 求对数函数的定义域
答案:AA.(-1,+∞)
C.(-1,1)∪(1,+∞)B.[-1,+∞)
D.[-1,1)∪(1,+∞)答案:C 求一些具体函数的定义域,有分母的要保证分
母不为零;开偶次方根的要保证被开方数为非负数;对数函数
的要保证真数大于零,底数大于零,且不等于 1.在求定义域的
过程中,往往需要解不等式(组),或利用函数的单调性.【变式与拓展】
1.(2014年江苏宿迁一模)函数f(x)=lg(2x-3x)的定义域为____________.(-∞,0)解析:要使函数有意义,则2x-3x>0,即2x>3x>0,题型 2 求对数函数的值域【例2】 已知y=log4(2x+3-x2).
(1)求 y 的定义域;(2)求 y 的单调区间;(3)求 y 的最大值,并求出对应的 x 值.解:(1)由2x+3-x2>0,解得-1∴f(x)的定义域为{x|-1(2)令u=2x+3-x2,则u>0,y=log4u.
由于u=2x+3-x2=-(x-1)2+4.
再考虑定义域可知,其增区间是(-1,1),减区间是[1,3).
又y=log4u在(0,+∞)上为增函数,
故该函数单调递增区间为(-1,1),单调递减区间为[1,3).
(3)∵u=2x+3-x2=-(x-1)2+4≤4,
∴y=log4u≤log44=1.
故当x=1,u取最大值4时,y取最大值1.【变式与拓展】A2.函数f(x)=log2(3x+1)的值域为( )
A.(0,+∞)
B.[0,+∞)
C.(1,+∞)
D.[1,+∞)解析:∵3x>0,3x+1>1,∴log2(3x+1)>0.3.求下列函数的值域:
(1)y=log2(x2+4);解:(1)y=log2(x2+4)的定义域是R.
∵x2+4≥4,∴log2(x2+4)≥log24=2.
∴y=log2(x2+4)的值域为{y|y≥2}.题型 3 利用函数性质比较大小
【例 3】 比较下列三组数的大小:作y=log7x与y=log6x图象,如图2-2-1.图 2-2-1 利用对数函数的单调性比较两个对数的大
小,常用的方法有:①若底数为同一常数,则可由对数函数的
单调性直接判断;②若底数为同一字母,则按对数函数的单调
性对底数进行分类讨论;③若底数不同,真数相同,则可用换
底公式化为同底,再进行比较;④若底数、真数都不相同,则
常借助 1,0 等中间量进行比较,或利用对数函数图象的性质进
行判断.【变式与拓展】DA.yC.1B.0.32<20.3<log20.3
C.log20.3<0.32<20.3
D.log20.3<20.3<0.32【例 4】 设函数 y=f(x),且 lg(lgy)=lg3x+lg(3-x),求:
(1)f(x)的表达式及定义域;
(2)f(x)的值域.
易错分析:求(2)时没有考虑所给式子的定义域的限制.
[方法·规律·小结]1.对数函数的概念. (1)同指数函数一样,对数函数仍然采用形式定义,只有形如y=logax(a>0,且a≠1)的函数才是对数函数,如y=2log2x,y=log2x2等都不是对数函数.
(2)由于指数函数y=ax(a>0,且a≠1)的定义域是R,值域为(0,+∞),所以对数函数y=logax(a>0,且a≠1)的定义域为(0,+∞),值域为R,它们互为反函数.2.比较两个对数的大小的基本方法.(1)若底数相同,真数不同,可构造相应的对数函数,利用其单调性比较大小.(2)若真数相同,底数不同,则可借助函数图象,利用图象在直线 x=1 右侧“底大图低”的特点比较大小.(3)若底数、真数均不相同,则经常借助中间值“0”或“1”比较大小. 3.对数运算的实质是把积、商和幂的对数转化为对数的和、
差和积,要注意公式应用的条件为 M>0,N>0.在讨论对数函数
的性质时,应注意定义域及底数的取值范围,必须时刻注意底
数 a>0,且 a≠1,若不清楚其取值范围,则应树立分类讨论的
数学思想,分 a>1 和 0
系,初步理解对数函数的概念,体会对数函数是一类重要的函
数模型.2.能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点. 1.对数函数
一般地,我们把函数 y=logax(a>0,且 a≠1)叫做对数函数,
其中________是自变量,函数的定义域是___________,值域是实数集 R.x(0,+∞)2.对数函数 y=logax(a>0,且 a≠1)的图象特征和性质(1,0)y>0y<0y<0y>0增减(续表)y1<y2y1>y2练习2:函数f(x)=log(a-1)x在(0,+∞)上单调递减,则实数 a 的取值范围为__________.1
(1)log108与log1015; (2)log0.50.9与log0.50.6.
答案:(1)log1015>log108;(2)log0.50.6>log0.50.9. 2.求下列函数的定义域:题型 1 求对数函数的定义域
答案:AA.(-1,+∞)
C.(-1,1)∪(1,+∞)B.[-1,+∞)
D.[-1,1)∪(1,+∞)答案:C 求一些具体函数的定义域,有分母的要保证分
母不为零;开偶次方根的要保证被开方数为非负数;对数函数
的要保证真数大于零,底数大于零,且不等于 1.在求定义域的
过程中,往往需要解不等式(组),或利用函数的单调性.【变式与拓展】
1.(2014年江苏宿迁一模)函数f(x)=lg(2x-3x)的定义域为____________.(-∞,0)解析:要使函数有意义,则2x-3x>0,即2x>3x>0,题型 2 求对数函数的值域【例2】 已知y=log4(2x+3-x2).
(1)求 y 的定义域;(2)求 y 的单调区间;(3)求 y 的最大值,并求出对应的 x 值.解:(1)由2x+3-x2>0,解得-1
由于u=2x+3-x2=-(x-1)2+4.
再考虑定义域可知,其增区间是(-1,1),减区间是[1,3).
又y=log4u在(0,+∞)上为增函数,
故该函数单调递增区间为(-1,1),单调递减区间为[1,3).
(3)∵u=2x+3-x2=-(x-1)2+4≤4,
∴y=log4u≤log44=1.
故当x=1,u取最大值4时,y取最大值1.【变式与拓展】A2.函数f(x)=log2(3x+1)的值域为( )
A.(0,+∞)
B.[0,+∞)
C.(1,+∞)
D.[1,+∞)解析:∵3x>0,3x+1>1,∴log2(3x+1)>0.3.求下列函数的值域:
(1)y=log2(x2+4);解:(1)y=log2(x2+4)的定义域是R.
∵x2+4≥4,∴log2(x2+4)≥log24=2.
∴y=log2(x2+4)的值域为{y|y≥2}.题型 3 利用函数性质比较大小
【例 3】 比较下列三组数的大小:作y=log7x与y=log6x图象,如图2-2-1.图 2-2-1 利用对数函数的单调性比较两个对数的大
小,常用的方法有:①若底数为同一常数,则可由对数函数的
单调性直接判断;②若底数为同一字母,则按对数函数的单调
性对底数进行分类讨论;③若底数不同,真数相同,则可用换
底公式化为同底,再进行比较;④若底数、真数都不相同,则
常借助 1,0 等中间量进行比较,或利用对数函数图象的性质进
行判断.【变式与拓展】DA.y
C.log20.3<0.32<20.3
D.log20.3<20.3<0.32【例 4】 设函数 y=f(x),且 lg(lgy)=lg3x+lg(3-x),求:
(1)f(x)的表达式及定义域;
(2)f(x)的值域.
易错分析:求(2)时没有考虑所给式子的定义域的限制.
[方法·规律·小结]1.对数函数的概念. (1)同指数函数一样,对数函数仍然采用形式定义,只有形如y=logax(a>0,且a≠1)的函数才是对数函数,如y=2log2x,y=log2x2等都不是对数函数.
(2)由于指数函数y=ax(a>0,且a≠1)的定义域是R,值域为(0,+∞),所以对数函数y=logax(a>0,且a≠1)的定义域为(0,+∞),值域为R,它们互为反函数.2.比较两个对数的大小的基本方法.(1)若底数相同,真数不同,可构造相应的对数函数,利用其单调性比较大小.(2)若真数相同,底数不同,则可借助函数图象,利用图象在直线 x=1 右侧“底大图低”的特点比较大小.(3)若底数、真数均不相同,则经常借助中间值“0”或“1”比较大小. 3.对数运算的实质是把积、商和幂的对数转化为对数的和、
差和积,要注意公式应用的条件为 M>0,N>0.在讨论对数函数
的性质时,应注意定义域及底数的取值范围,必须时刻注意底
数 a>0,且 a≠1,若不清楚其取值范围,则应树立分类讨论的
数学思想,分 a>1 和 0
