高一数学2.3 幂函数

课件21张PPT。2.3 幂函数【学习目标】1.通过具体实例了解幂函数的图象和性质.2.体会幂函数的变化规律及蕴含其中的对称性并能进行简单的应用.1.幂函数的定义xα 形如________________的函数称为幂函数，其中______是
自变量，______为常数.①⑥练习 1：下列函数中是幂函数的是__________.
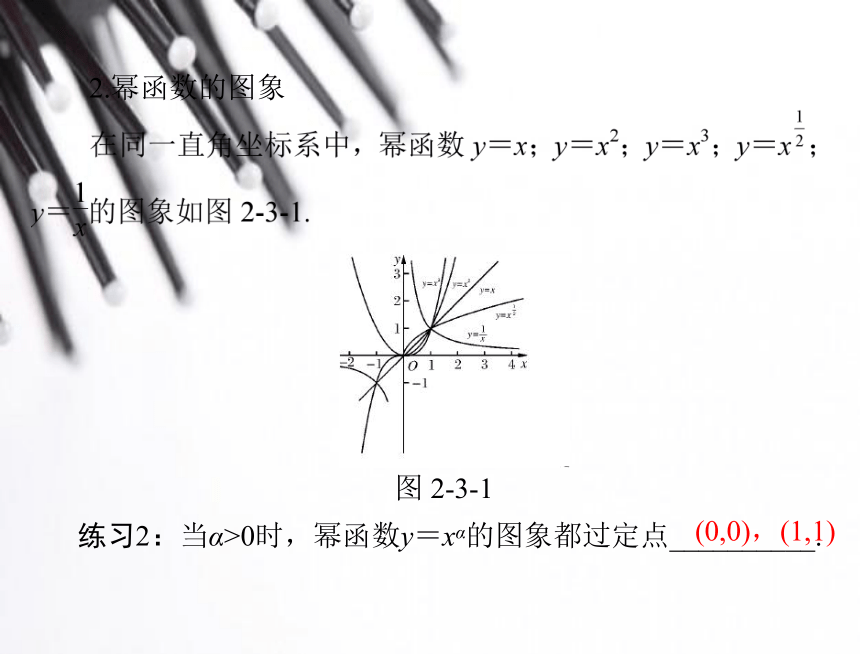
y＝xα(α∈R)2.幂函数的图象(0,0)，(1,1)图 2-3-1练习2：当α>0时，幂函数y＝xα的图象都过定点__________. 3.幂函数的性减小无限接近 练习3：当α<0时，当x∈(0，＋∞)时，y＝xa的函数值随x的增大而______，向右图象与x轴____________.【问题探究】函数 y＝ax(a>0，且 a≠1)是指数函数，函数 y＝xα是幂函数，两种函数最大的区别是什么？答案：指数函数的指数是变量，而幂函数是底数为变量．题型 1 幂函数的定义及应用(0， ＋∞)上是增函数，判断函数 f(x)的奇偶性.
思维突破：根据幂函数的特点、函数奇偶性的定义进行解
题.(1)幂函数 y＝xα的特点：①系数必须为 1；②指数必须为常数.(2)幂函数的单调性：①α>0 时，y＝xα在(0，＋∞)上为增函数；②α<0 时，y＝xα在(0，＋∞)上为减函数.【变式与拓展】(1)幂函数？
(2)正比例函数？
(3)反比例函数？
(4)二次函数？题型 2 幂函数的图象答案：B【变式与拓展】
2.(2013 年四川乐山一模)下面给出 4 个幂函数的图象，则)B图象与函数的大致对应是(
题型 3 函数值的大小比较A.aa＜ab＜ba
B.aa＜ba＜ab
C.ab＜aa＜ba
D.ab＜ba＜aa答案：C 比较两个幂的大小，如果指数相同而底数不同
(即底数为变量)，此时利用幂函数的单调性来比较大小；如果
底数相同而指数不同(即指数为变量)，此时利用指数函数的单
调性来比较大小；如果两个幂指数、底数全不同，此时需要引
入中间变量，常用的中间变量有 0,1 或由一个幂的底数和另一
个幂的指数组成的幂.注意：指数函数当 a>1 时单调递增，当
00 时在第一象限单调递增，
当α<0 时在第一象限单调递减.【变式与拓展】3.下列各不等式中正确的是()D轴都无交点，且关于 y 轴对称，试确定 f(x)的解析式.
易错分析：对幂函数 y＝xα的理解不透彻.[方法·规律·小结]
1.幂函数的概念.2.幂函数y＝xα的性质是分α>0和α<0两种情况来讨论的. 形如y＝xα的函数叫幂函数，这里需有：①系数为1，②指数为常数，③后面不加任何项.例如：y＝3x，y＝xx＋1，y＝x2＋1均不是幂函数，再者注意与指数函数的区别，如y＝x2是幂函数，y＝2x是指数函数. 3.幂函数的图象一定会出现在第一象限，一定不会出现在
第四象限，至于是否出现在第二、三象限，要看函数的奇偶性，
作幂函数的图象要联系函数的定义域、值域、单调性、奇偶性
等，只要作出幂函数在第一象限的图象，然后根据它的奇偶性
就可作出幂函数在定义域内完整的图象.