3.2.2奇偶性 教学设计
文档属性
| 名称 | 3.2.2奇偶性 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 137.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览

文档简介
函数的奇偶性教学设计
学情分析
这节内容学生在初中虽然没有学过,但是已经学习过具有奇偶性的具体函数:正比例函数,反比例函数,二次函数。故可以在此基础上,引入奇、偶函数的概念,以便于学生理解。在引入概念时始终结合具体函数的图像,以增加直观性,这样更符合学生的认知规律,同时为阐述奇、偶函数的几何特征埋下伏笔。对于概念可从代数特征与几何特征两个角度去分析,让学生理解:奇函数、偶函数的定义域是关于原点对称的非空数集;同时让学生了解并不是所有的函数都具有奇偶性,也有可能是非奇非偶函数。关于单调性与奇偶性关系,引导学生拓展延伸,可以取得理想效果。
教材分析
与函数单调性不同,函数的奇偶性是函数的整体性质,即它要求定义域中任意一个自变量都具有这样的特性。教科书在处理函数的奇偶性时,沿用了处理函数单调性的方法,即先给出几个特殊函数的图像,让学生获得奇偶性的直观定性认识;然后利用表格研究发现数量变化特征;最后通过代数运算,验证发现的数量特征的普遍性,在此基础上建立奇(偶)函数概念。因此教学时,充分利用信息技术创设教学情境,会使数与形的结合更自然。
值得注意的问题:对于奇函数,教材在给出的表格中留出大部分空格,皆在让学生自己动手计算填写数据,仿照偶函数概念建立的过程,独立地去经历发现、猜想与证明的全过程,从而建立奇函数的概念。教学时,可以通过具体例子引导学生认识、并不是所有的函数都具有奇偶性,如函数即不是奇函数也不是偶函数,可以通过图像看出也可以通过定义去说明
教学目标
知识与技能目标
理解函数奇偶性及其几何意义,培养学生观察、抽象能力,以及从特殊到一般的概括、归纳问题的能力。
过程与方法目标
学会运用函数图像理解和研究函数的性质,掌握判断函数的奇偶性的方法,渗透数形结合的数学思想。
情感与态度目标
通过函数奇偶性的教学,培养学生从特使到一般的概括归纳问题能力。
教学重难点
教学重点:函数的奇偶性及其几何意义
教学难点:判断函数奇偶性的方法与格式
教学过程
创设情境,揭示课题
对称是大自然的一种美,首先让我们一起来欣赏几幅图片,在生活中我们常常能看到一些对称的建筑,以及一些对称图形,他们都给我们很美的享受。我们把这些图形分为两类,一类是轴对称图形,一类是中心对称图形。其实,我们数学当中也有这种对称之美,今天让我们一起来学习函数图像中的对称美。
设计意图:同学们处于高一的适应阶段,通过提及初中所学的知识,即起到初高中衔接,又能够带来一些亲切感。通过展示大自然的图片,吸引同学们的注意,同时也能丰富数学课的元素,引出今天学习的内容函数的奇偶性。
概念生成
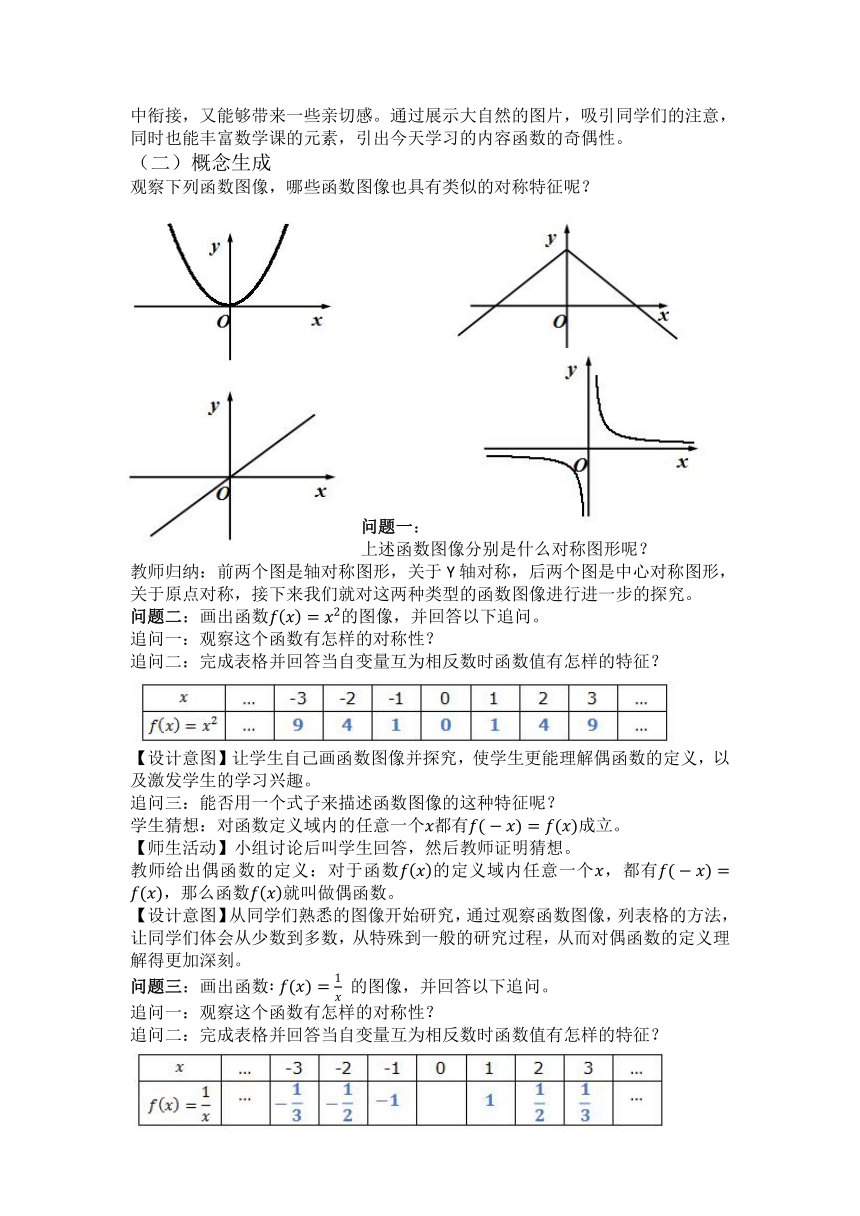
观察下列函数图像,哪些函数图像也具有类似的对称特征呢?
问题一:上述函数图像分别是什么对称图形呢?
教师归纳:前两个图是轴对称图形,关于Y轴对称,后两个图是中心对称图形,关于原点对称,接下来我们就对这两种类型的函数图像进行进一步的探究。
问题二:画出函数的图像,并回答以下追问。
追问一:观察这个函数有怎样的对称性?
追问二:完成表格并回答当自变量互为相反数时函数值有怎样的特征?
【设计意图】让学生自己画函数图像并探究,使学生更能理解偶函数的定义,以及激发学生的学习兴趣。
追问三:能否用一个式子来描述函数图像的这种特征呢?
学生猜想:对函数定义域内的任意一个都有成立。
【师生活动】小组讨论后叫学生回答,然后教师证明猜想。
教师给出偶函数的定义:对于函数的定义域内任意一个,都有,那么函数就叫做偶函数。
【设计意图】从同学们熟悉的图像开始研究,通过观察函数图像,列表格的方法,让同学们体会从少数到多数,从特殊到一般的研究过程,从而对偶函数的定义理解得更加深刻。
问题三:画出函数 的图像,并回答以下追问。
追问一:观察这个函数有怎样的对称性?
追问二:完成表格并回答当自变量互为相反数时函数值有怎样的特征?
【设计意图】让学生自己画函数图像并探究,使学生更能理解奇函数的定义,以及激发学生的学习兴趣。
追问三:能否用一个式子来描述函数图像的这种特征呢?
学生猜想:对函数定义域内的任意一个都有成立。
【师生活动】小组讨论后叫学生回答,然后教师证明猜想。
教师给出奇函数的定义:对于函数的定义域内任意一个,都有,那么函数就叫做奇函数。
【设计意图】从同学们熟悉的图像开始研究,通过观察函数图像,列表格的方法,让同学们体会从少数到多数,从特殊到一般的研究过程,从而对奇函数的定义理解得更加深刻。教师引导过程中突出每一个,都有一个与其对应。剖析概念,深挖函数奇偶性概念的本质,帮助同学更好的理解函数的奇偶性。
概念判断
问题四:现在我们对函数的奇偶性有了更深层次的理解,请你判断下列函数是奇函数还是偶函数呢?
【师生活动】教师叫学生独立思考,然后叫学生回答,最后教师总结
【设计意图】通过这个练习,加深学生对奇函数,偶函数定义的理解,让学生学会看图判断是奇函数,还是偶函数。奇函数关于原点对称,偶函数关于y轴对称。同时强调奇函数和偶函数的定义域都必须关于原点对称。
问题五:判断函数的奇偶性.
【师生活动】教师叫学生独立思考,然后叫一名学生上黑板板书。
【设计意图】通过一个例题让学生学会用定义法判断函数的奇偶性,并且学会做题的书写格式。
追问一:如果函数改为那么还是偶函数吗?
【师生活动】学生们自主探究讨论,教师总结。
【设计意图】再次强调了奇函数,偶函数的定义域都关于原点对称,在做题前应当先判断这一步。
教师总结用定义判断函数奇偶性的做题方法:
第一步:求出函数的定义域。
第二步:判断函数的定义域是否关于原点对称,若否,则函数既不是奇函数也不是偶函数,结束判断;若是,则进行第三步。
第三步:(为定义域),计算
若,则为偶函数
若,则为奇函数;
若且,则即不是奇函数也不是偶函数。
若且,则既是奇函数也是偶函数。
巩固练习,概念运用
例一:判断下列函数的奇偶性
【师生活动】学生自己在本子上练习,教师下讲台巡视指导,叫同学示范板书正确答案。
【设计意图】通过几道题目让学生学会用定义判断函数的奇偶性,并且让学生意识到不是所有的函数都具有奇偶性,有的函数既不是奇函数也不是偶函数,有的函数既是奇函数又是偶函数。
例二: 已知函数是奇函数,如图是函数 在y轴右侧的图象,请根据函数奇偶性画出它在y轴左侧的图象。
【师生活动】学生自己在图纸上画,教师对答案
【设计意图】让学生知道奇函数关于原点对称,偶函数关于y轴对称。
课堂小结
本节课主要学习了函数奇偶性,判断函数的奇偶性通常有两种方法,即定义法和图像法,用定义法判断函数的奇偶性时,必须注意首先判断函数的定义域是否关于原点对称。
板书设计
学情分析
这节内容学生在初中虽然没有学过,但是已经学习过具有奇偶性的具体函数:正比例函数,反比例函数,二次函数。故可以在此基础上,引入奇、偶函数的概念,以便于学生理解。在引入概念时始终结合具体函数的图像,以增加直观性,这样更符合学生的认知规律,同时为阐述奇、偶函数的几何特征埋下伏笔。对于概念可从代数特征与几何特征两个角度去分析,让学生理解:奇函数、偶函数的定义域是关于原点对称的非空数集;同时让学生了解并不是所有的函数都具有奇偶性,也有可能是非奇非偶函数。关于单调性与奇偶性关系,引导学生拓展延伸,可以取得理想效果。
教材分析
与函数单调性不同,函数的奇偶性是函数的整体性质,即它要求定义域中任意一个自变量都具有这样的特性。教科书在处理函数的奇偶性时,沿用了处理函数单调性的方法,即先给出几个特殊函数的图像,让学生获得奇偶性的直观定性认识;然后利用表格研究发现数量变化特征;最后通过代数运算,验证发现的数量特征的普遍性,在此基础上建立奇(偶)函数概念。因此教学时,充分利用信息技术创设教学情境,会使数与形的结合更自然。
值得注意的问题:对于奇函数,教材在给出的表格中留出大部分空格,皆在让学生自己动手计算填写数据,仿照偶函数概念建立的过程,独立地去经历发现、猜想与证明的全过程,从而建立奇函数的概念。教学时,可以通过具体例子引导学生认识、并不是所有的函数都具有奇偶性,如函数即不是奇函数也不是偶函数,可以通过图像看出也可以通过定义去说明
教学目标
知识与技能目标
理解函数奇偶性及其几何意义,培养学生观察、抽象能力,以及从特殊到一般的概括、归纳问题的能力。
过程与方法目标
学会运用函数图像理解和研究函数的性质,掌握判断函数的奇偶性的方法,渗透数形结合的数学思想。
情感与态度目标
通过函数奇偶性的教学,培养学生从特使到一般的概括归纳问题能力。
教学重难点
教学重点:函数的奇偶性及其几何意义
教学难点:判断函数奇偶性的方法与格式
教学过程
创设情境,揭示课题
对称是大自然的一种美,首先让我们一起来欣赏几幅图片,在生活中我们常常能看到一些对称的建筑,以及一些对称图形,他们都给我们很美的享受。我们把这些图形分为两类,一类是轴对称图形,一类是中心对称图形。其实,我们数学当中也有这种对称之美,今天让我们一起来学习函数图像中的对称美。
设计意图:同学们处于高一的适应阶段,通过提及初中所学的知识,即起到初高中衔接,又能够带来一些亲切感。通过展示大自然的图片,吸引同学们的注意,同时也能丰富数学课的元素,引出今天学习的内容函数的奇偶性。
概念生成
观察下列函数图像,哪些函数图像也具有类似的对称特征呢?
问题一:上述函数图像分别是什么对称图形呢?
教师归纳:前两个图是轴对称图形,关于Y轴对称,后两个图是中心对称图形,关于原点对称,接下来我们就对这两种类型的函数图像进行进一步的探究。
问题二:画出函数的图像,并回答以下追问。
追问一:观察这个函数有怎样的对称性?
追问二:完成表格并回答当自变量互为相反数时函数值有怎样的特征?
【设计意图】让学生自己画函数图像并探究,使学生更能理解偶函数的定义,以及激发学生的学习兴趣。
追问三:能否用一个式子来描述函数图像的这种特征呢?
学生猜想:对函数定义域内的任意一个都有成立。
【师生活动】小组讨论后叫学生回答,然后教师证明猜想。
教师给出偶函数的定义:对于函数的定义域内任意一个,都有,那么函数就叫做偶函数。
【设计意图】从同学们熟悉的图像开始研究,通过观察函数图像,列表格的方法,让同学们体会从少数到多数,从特殊到一般的研究过程,从而对偶函数的定义理解得更加深刻。
问题三:画出函数 的图像,并回答以下追问。
追问一:观察这个函数有怎样的对称性?
追问二:完成表格并回答当自变量互为相反数时函数值有怎样的特征?
【设计意图】让学生自己画函数图像并探究,使学生更能理解奇函数的定义,以及激发学生的学习兴趣。
追问三:能否用一个式子来描述函数图像的这种特征呢?
学生猜想:对函数定义域内的任意一个都有成立。
【师生活动】小组讨论后叫学生回答,然后教师证明猜想。
教师给出奇函数的定义:对于函数的定义域内任意一个,都有,那么函数就叫做奇函数。
【设计意图】从同学们熟悉的图像开始研究,通过观察函数图像,列表格的方法,让同学们体会从少数到多数,从特殊到一般的研究过程,从而对奇函数的定义理解得更加深刻。教师引导过程中突出每一个,都有一个与其对应。剖析概念,深挖函数奇偶性概念的本质,帮助同学更好的理解函数的奇偶性。
概念判断
问题四:现在我们对函数的奇偶性有了更深层次的理解,请你判断下列函数是奇函数还是偶函数呢?
【师生活动】教师叫学生独立思考,然后叫学生回答,最后教师总结
【设计意图】通过这个练习,加深学生对奇函数,偶函数定义的理解,让学生学会看图判断是奇函数,还是偶函数。奇函数关于原点对称,偶函数关于y轴对称。同时强调奇函数和偶函数的定义域都必须关于原点对称。
问题五:判断函数的奇偶性.
【师生活动】教师叫学生独立思考,然后叫一名学生上黑板板书。
【设计意图】通过一个例题让学生学会用定义法判断函数的奇偶性,并且学会做题的书写格式。
追问一:如果函数改为那么还是偶函数吗?
【师生活动】学生们自主探究讨论,教师总结。
【设计意图】再次强调了奇函数,偶函数的定义域都关于原点对称,在做题前应当先判断这一步。
教师总结用定义判断函数奇偶性的做题方法:
第一步:求出函数的定义域。
第二步:判断函数的定义域是否关于原点对称,若否,则函数既不是奇函数也不是偶函数,结束判断;若是,则进行第三步。
第三步:(为定义域),计算
若,则为偶函数
若,则为奇函数;
若且,则即不是奇函数也不是偶函数。
若且,则既是奇函数也是偶函数。
巩固练习,概念运用
例一:判断下列函数的奇偶性
【师生活动】学生自己在本子上练习,教师下讲台巡视指导,叫同学示范板书正确答案。
【设计意图】通过几道题目让学生学会用定义判断函数的奇偶性,并且让学生意识到不是所有的函数都具有奇偶性,有的函数既不是奇函数也不是偶函数,有的函数既是奇函数又是偶函数。
例二: 已知函数是奇函数,如图是函数 在y轴右侧的图象,请根据函数奇偶性画出它在y轴左侧的图象。
【师生活动】学生自己在图纸上画,教师对答案
【设计意图】让学生知道奇函数关于原点对称,偶函数关于y轴对称。
课堂小结
本节课主要学习了函数奇偶性,判断函数的奇偶性通常有两种方法,即定义法和图像法,用定义法判断函数的奇偶性时,必须注意首先判断函数的定义域是否关于原点对称。
板书设计
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
