8.3 同底数幂的除法(第1课时)

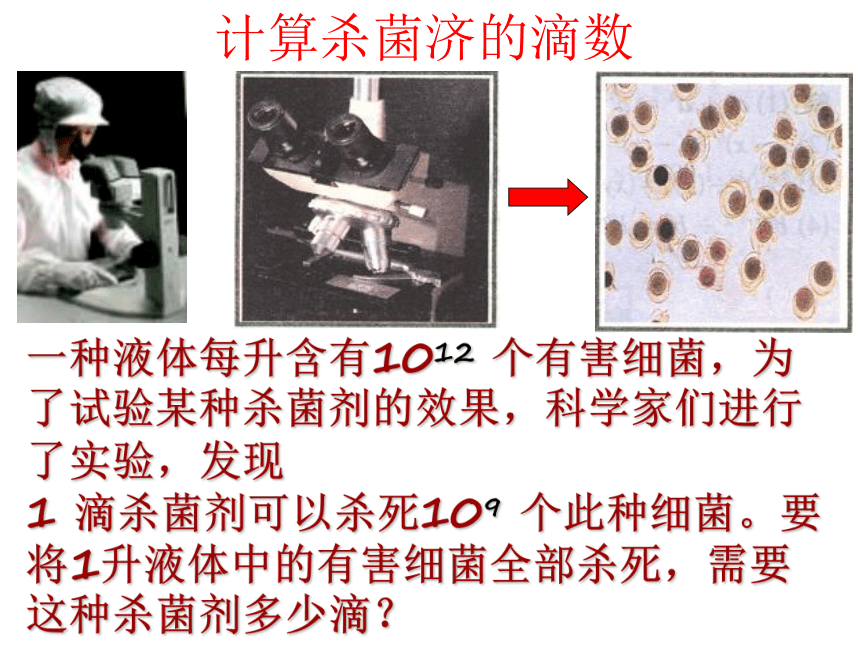
课件18张PPT。同底数幂的除法（１）计算杀菌济的滴数一种液体每升含有1012 个有害细菌，为了试验某种杀菌剂的效果，科学家们进行了实验，发现
1 滴杀菌剂可以杀死109 个此种细菌。要将1升液体中的有害细菌全部杀死，需要这种杀菌剂多少滴？一种液体每升含有1012 个有害细菌，为了试验某种杀菌剂的效果，科学家们进行了实验，发现
1 滴杀菌剂可以杀死109 个此种细菌。要将1升液体中的有害细菌全部杀死，需要这种杀菌剂多少滴？需要滴数：1012÷109=?103∵109×103=1012用 逆运算与同底数幂的乘法 来计算计算下列各式：
（1）108 ÷105
（2）10m÷10n
（3）(–3)m÷(–3)n103 ;m–n10m–n ;m–n(–3)m–n ;猜想｛am–n3am÷an=同底数幂的 除法法则am÷an= （a≠0, m、n都是正整数，且m>n）同底数幂相除，底数_____, 指数______. am–n不变相减∴ am÷an=
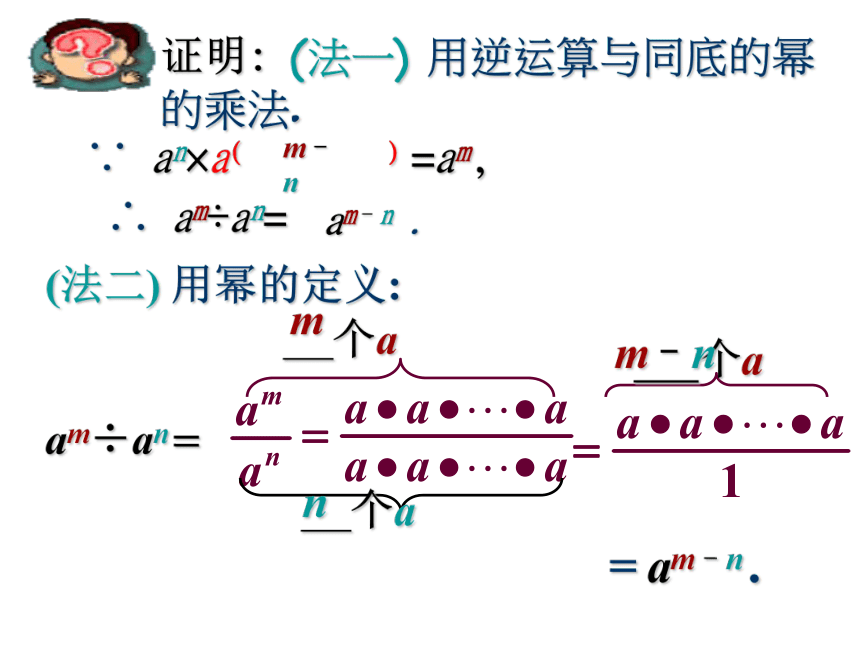
证明: (法一) 用逆运算与同底的幂的乘法.
m–nam–n .(法二) 用幂的定义:

am÷an= 个amnm–n= am–n .例题解析例题解析计算：
(1) a7÷a4 ; (2) (-x)6÷(-x)3;
(3) (xy)4÷(xy) ; (4) b2m+2÷b2 . = a7–4 = a3 ;(1) a7÷a4 解：(2) (-x)6÷(-x)3= (-x)6–3 = (-x)3(3) (xy)4÷(xy) =(xy)4–1(4) b2m+2÷b2 = b2m+2 – 2= -x3 ;=(xy)3=x3y3= b2m .例题解析. .最后结果中幂的形式应是最简的.① 幂的指数、底数都应是最简的；③ 幂的底数是积的形式时，要再用一次(ab)n=an an.②底数中系数不能为负；练 一 练：计算：1.m10÷(-m)4 2.(-b)9÷ (-b)6
3.(ab)8÷(-ab)2 4.t2m+3÷t2m-3(m为正整数)课本:
58页 1～3随堂练习：(1)（x+y）6÷(x+y)5·(y+x)7
?
? ?
?计算:(5)(3y-2x)3·(2x-3y)2n+1÷(3y-2x)2n+2(4)(m-n)9÷(n-m)8·(m-n)2(3)(-a-b)5÷(a+b)(2)(a-2)14÷(2-a)5要细心哦 !!!每一小题的底数均有不同，不能直接用同底数幂的法则，必须适当变形，使底数变为相同再计算。
? ? (3)(-a-b)5÷(a+b)
=[-(a+b)]5÷(a+b)
=-(a+b)5÷(a+b)
=-(a+b)5-1
=-(a+b)4
?(2)(a-2)14÷(2-a)5
=(2-a)14÷(2-a)5
=(2-a)14-5
=(2-a)9(1)（x+y)6÷(x+y)5·(y+x)7
=(x+y)6÷(x+y)5(x+y)7
=(x+y)6-5+7
=(x+y)8(4)(m-n)9÷(n-m)8·(m-n)2
=(m-n)9÷(m-n)8·(m-n)2
=(m-n)9-8+2
=(m-n)3
?(5)(3y-2x)3·(2x-3y)2n+1÷(3y-2x)2n+2
=(3y-2x)3·[-(3y-2x)2n+1]÷(3y-2x)2n+2
=-(3y-2x)3+(2n+1)-(2n+2)
=-(3y-2x)21.解关于x的方程：xm+3÷xm+1=x2+3x-52.若33·9m+4÷272m-1的值为729，求m的值。拓展本节课你的收获是什么？小结本节课你学到了什么?作业P62 习题 9.3 1..计算：
①a8÷a3÷a2
?②(-x)n+3÷(-x)n+1
?③(y3)4÷(y3·y2)2
④(a+b)3·(b+a)2÷(a+b)4
? ;
?⑥[(m-n)8÷(n-m)6]·(m-n)3
?⑦(a-b)5÷(b-a)3·(a-b)4
⑧ [(ab)4·(ab)5÷(ab)7]3