多边形的内角和[下学期]
图片预览


文档简介
课 题: 7.3.2多边形的内角和
课 型:公开课
三维目标:
(1) 知识与技能
(1) 掌握多边形的内角、外角的定义;
(2) 掌握多边形的内角和与外角和.
(2) 过程与方法
能通过不同的方法探索多边形的内角和与外角和公式, 并学会应用它们进行有关的计算.
(3) 情感、态度与价值观
渗透化归的数学思想方法;培养学生勤思、认真和勇于探索的精神.
教学重点:(1)多边形的内角和公式;
(2)多边形的外角和等于360度.
教学难点:多边形内角和定理的推导.
教学过程:
(一)创设情境,引入新课.
1、多边形的定义.
师:上一节课我们学习了多边形,怎样的图形称为多边形呢?
生:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
2、三角形内角和定理
师:今天这节课我们来研究多边形的内角和.(课题)
最简单的多边形是三角形.前面,我们学过了三角形,
三角形的内角和等于……?
生:180度.
师:长方形的内角和是多少度?
生:因为长方形有四个直角,所以长方形的内角和等于360度.
师:很好.
2、探索一般四边形的内角和.
师:那一般的四边形呢?
生:也是360度.
师:为什么呢?我们先用几何画板来验证一下.(用几何画板验证四边形内角和等于360度)
师:刚才我们已经验证了四边形的内角和确实等于360度,那到底是为什么呢?
(二)合作交流,解读探究.
1、证明四边形的内角和等于360度.
生:作出四边形的一条对角线,它将四边形分成两个三角形,因为三角形的内角和等于180度,所以,四边形的内角和等于360度.
师:很好!“生A”,你能告诉我他解决这个问题的思想是什么?
生A:将四边形分割成三角形,利用三角形的内角和来求.
师:非常好!那五边形、六边形、……、n边形呢?
生:可以用同样的方法.
2、探索多边形内角和.
活动1:
1、从五边形的一个顶点出发,可以引 2 条对角线,它们将五边形分为 3 个三角形,
所以,五边形的内角和等于180°× 3 .
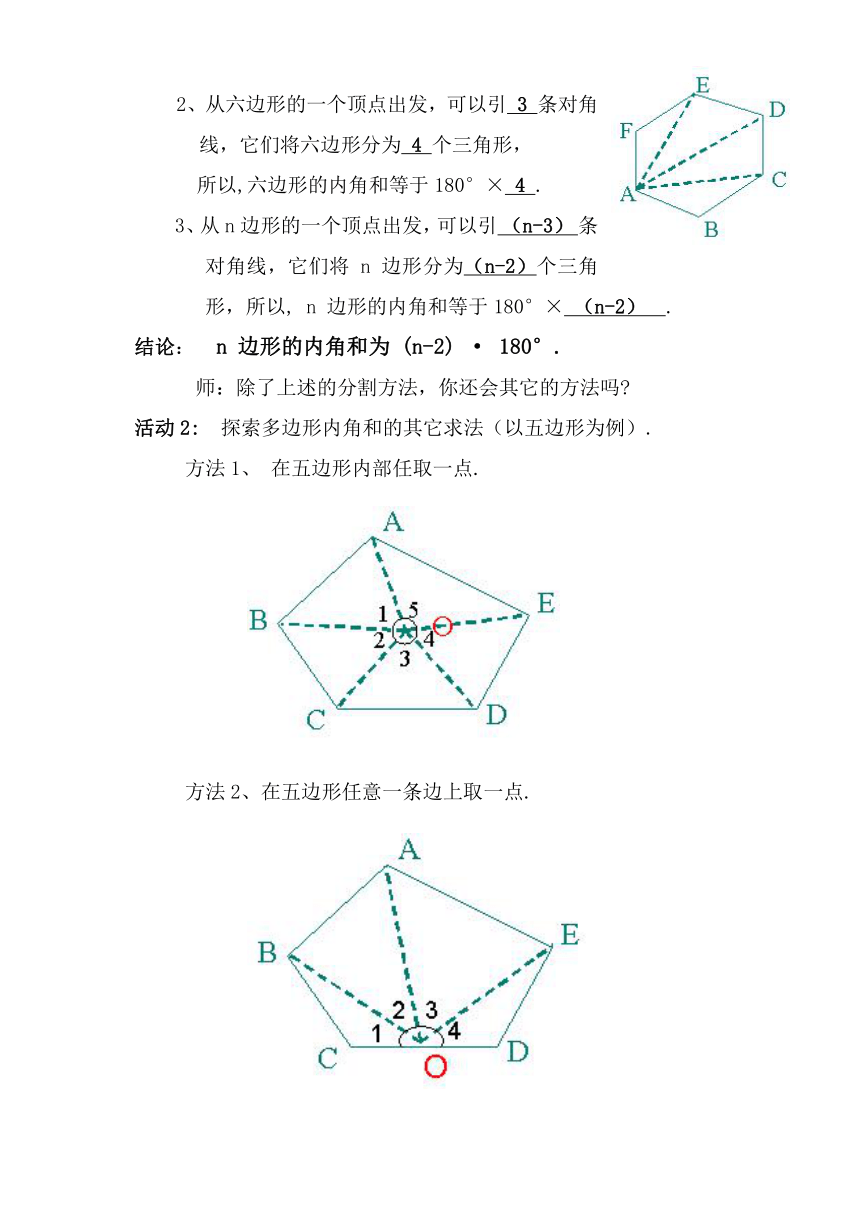
2、从六边形的一个顶点出发,可以引 3 条对角线,它们将六边形分为 4 个三角形,
所以,六边形的内角和等于180°× 4 .
3、从n边形的一个顶点出发,可以引 (n-3) 条对角线,它们将 n 边形分为(n-2)个三角形,所以, n 边形的内角和等于180°× (n-2) .
结论: n 边形的内角和为 (n-2) · 180°.
师:除了上述的分割方法,你还会其它的方法吗
活动2: 探索多边形内角和的其它求法(以五边形为例).
方法1、 在五边形内部任取一点.
方法2、在五边形任意一条边上取一点.
小练习:
(1)填空题:
①多边形的内角和随着边数的增加而增加,边数增加一条时,它的内角和增加180度.
②七边形的内角和等于900度.
③一个多边形的内角和等于720 °,那么这个多边形是六边形.
④如果一个四边形的一组对角互补, 那么另一组对角 也互补 .
3、探索多边形的外角和.
例1.如图,在六边形的每一个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少度?
解:如图,六边形ABCDEF中,
∠1+∠7=180 °,∠2+∠8=180 °,
∠3+∠9=180 °,∠4+∠10=180 °,
∠5+∠11=180 °,∠6+∠12=180 °.
∵ ∠7+∠8+∠9+∠10 +∠11+∠12 =(6-2)×180 °= 720°,
∴ ∠1+∠2+∠3+∠4+∠5+∠6 = 6×180 °-720 °= 360°.
对于 n 边形,结论仍然成立!
结论:多边形的外角和等于360°.
用动画展示,使用平移的方法得到六边形的内角和为360度.
小练习:
(1)判断题:
①当多边形的边数增加时,它的外角和也随着增加.(错误)
说明:多边形的边数的变化不改变多边形的外角和,
但改变多边形的内角和.
②正六边形的每个外角都等于60度.(正确)
(2)填空题:
①正九边形的每一个外角都等于40度.
②一个多边形的每一个外角都等于30°,这个多边形是十二边形.
(三)巩固提高
1. 求下列图形中 x 的值:
2. 八边形的内角和等于1080度.
3.一个多边形的内角和等于1260° ,则这个多边形是 九 边形.
4.一个正多边形的每一个内角都等于135°,则这个多边形是正 八 边形.
5.若一个多边形的内角和等于外角和,这个则多边形是 四 边形。
(四)总结反思
师:这节课,你学到了什么?
生1:如何用分割的方法求多边形的内角和.
生2:n 边形的内角和等于 (n-2) · 180°.
生3:多边形的外角和等于360°.
生4:研究一般多边形的内角和,我们可以从四边形开始研究,
由特殊到一般.
(五)课后作业
1、作业卷16
2、《课时作业本》P.47
课 型:公开课
三维目标:
(1) 知识与技能
(1) 掌握多边形的内角、外角的定义;
(2) 掌握多边形的内角和与外角和.
(2) 过程与方法
能通过不同的方法探索多边形的内角和与外角和公式, 并学会应用它们进行有关的计算.
(3) 情感、态度与价值观
渗透化归的数学思想方法;培养学生勤思、认真和勇于探索的精神.
教学重点:(1)多边形的内角和公式;
(2)多边形的外角和等于360度.
教学难点:多边形内角和定理的推导.
教学过程:
(一)创设情境,引入新课.
1、多边形的定义.
师:上一节课我们学习了多边形,怎样的图形称为多边形呢?
生:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
2、三角形内角和定理
师:今天这节课我们来研究多边形的内角和.(课题)
最简单的多边形是三角形.前面,我们学过了三角形,
三角形的内角和等于……?
生:180度.
师:长方形的内角和是多少度?
生:因为长方形有四个直角,所以长方形的内角和等于360度.
师:很好.
2、探索一般四边形的内角和.
师:那一般的四边形呢?
生:也是360度.
师:为什么呢?我们先用几何画板来验证一下.(用几何画板验证四边形内角和等于360度)
师:刚才我们已经验证了四边形的内角和确实等于360度,那到底是为什么呢?
(二)合作交流,解读探究.
1、证明四边形的内角和等于360度.
生:作出四边形的一条对角线,它将四边形分成两个三角形,因为三角形的内角和等于180度,所以,四边形的内角和等于360度.
师:很好!“生A”,你能告诉我他解决这个问题的思想是什么?
生A:将四边形分割成三角形,利用三角形的内角和来求.
师:非常好!那五边形、六边形、……、n边形呢?
生:可以用同样的方法.
2、探索多边形内角和.
活动1:
1、从五边形的一个顶点出发,可以引 2 条对角线,它们将五边形分为 3 个三角形,
所以,五边形的内角和等于180°× 3 .
2、从六边形的一个顶点出发,可以引 3 条对角线,它们将六边形分为 4 个三角形,
所以,六边形的内角和等于180°× 4 .
3、从n边形的一个顶点出发,可以引 (n-3) 条对角线,它们将 n 边形分为(n-2)个三角形,所以, n 边形的内角和等于180°× (n-2) .
结论: n 边形的内角和为 (n-2) · 180°.
师:除了上述的分割方法,你还会其它的方法吗
活动2: 探索多边形内角和的其它求法(以五边形为例).
方法1、 在五边形内部任取一点.
方法2、在五边形任意一条边上取一点.
小练习:
(1)填空题:
①多边形的内角和随着边数的增加而增加,边数增加一条时,它的内角和增加180度.
②七边形的内角和等于900度.
③一个多边形的内角和等于720 °,那么这个多边形是六边形.
④如果一个四边形的一组对角互补, 那么另一组对角 也互补 .
3、探索多边形的外角和.
例1.如图,在六边形的每一个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少度?
解:如图,六边形ABCDEF中,
∠1+∠7=180 °,∠2+∠8=180 °,
∠3+∠9=180 °,∠4+∠10=180 °,
∠5+∠11=180 °,∠6+∠12=180 °.
∵ ∠7+∠8+∠9+∠10 +∠11+∠12 =(6-2)×180 °= 720°,
∴ ∠1+∠2+∠3+∠4+∠5+∠6 = 6×180 °-720 °= 360°.
对于 n 边形,结论仍然成立!
结论:多边形的外角和等于360°.
用动画展示,使用平移的方法得到六边形的内角和为360度.
小练习:
(1)判断题:
①当多边形的边数增加时,它的外角和也随着增加.(错误)
说明:多边形的边数的变化不改变多边形的外角和,
但改变多边形的内角和.
②正六边形的每个外角都等于60度.(正确)
(2)填空题:
①正九边形的每一个外角都等于40度.
②一个多边形的每一个外角都等于30°,这个多边形是十二边形.
(三)巩固提高
1. 求下列图形中 x 的值:
2. 八边形的内角和等于1080度.
3.一个多边形的内角和等于1260° ,则这个多边形是 九 边形.
4.一个正多边形的每一个内角都等于135°,则这个多边形是正 八 边形.
5.若一个多边形的内角和等于外角和,这个则多边形是 四 边形。
(四)总结反思
师:这节课,你学到了什么?
生1:如何用分割的方法求多边形的内角和.
生2:n 边形的内角和等于 (n-2) · 180°.
生3:多边形的外角和等于360°.
生4:研究一般多边形的内角和,我们可以从四边形开始研究,
由特殊到一般.
(五)课后作业
1、作业卷16
2、《课时作业本》P.47
