9.2 单项式乘多项式[下学期]

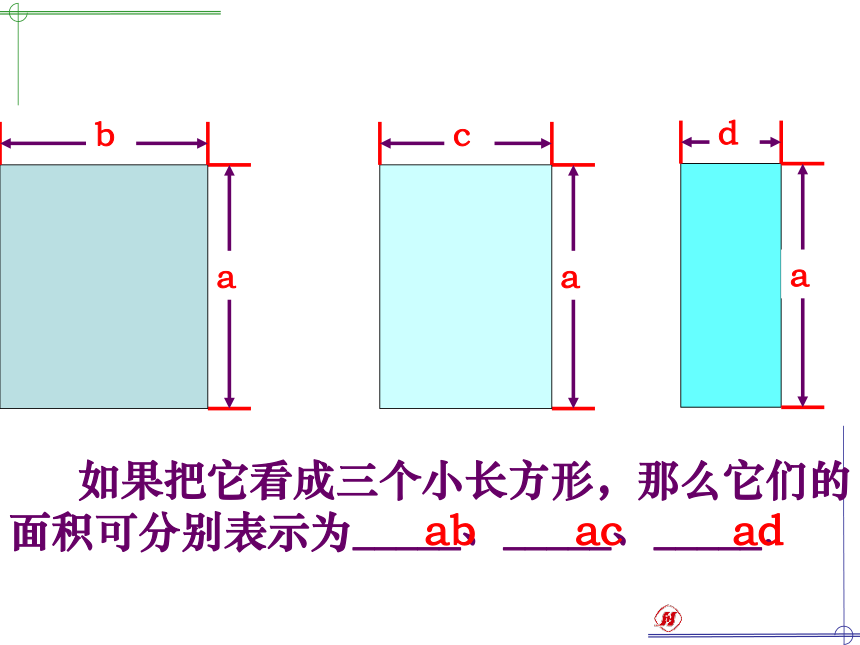
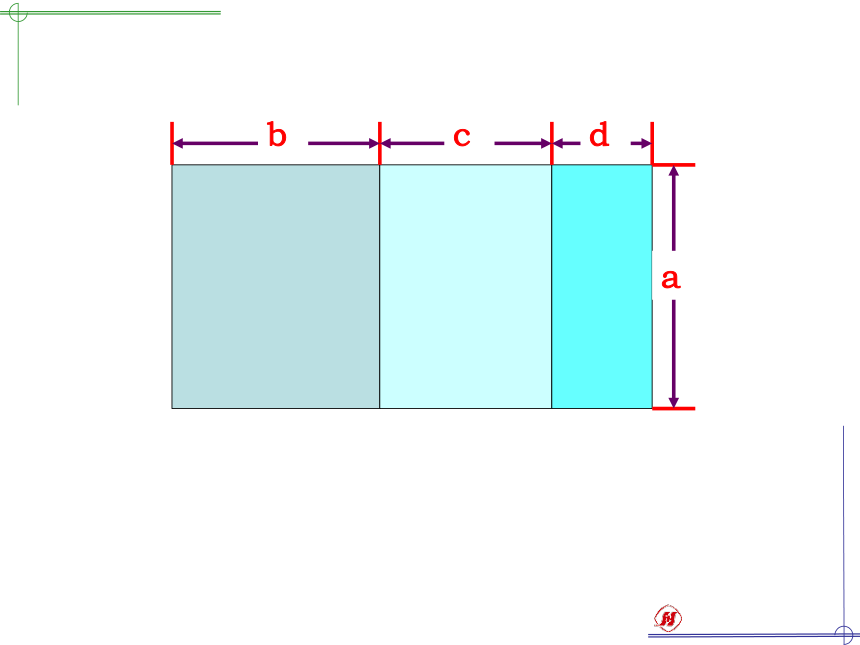
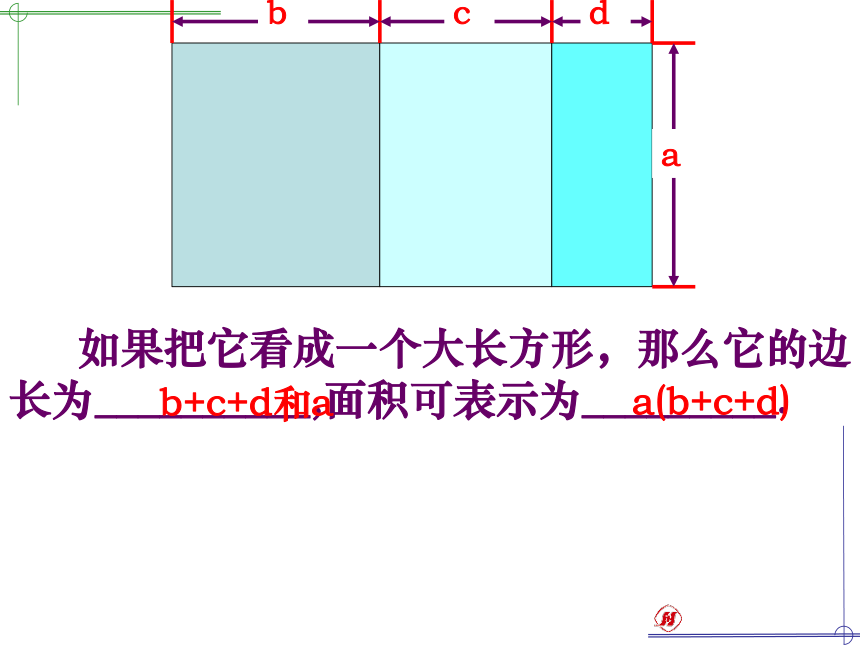
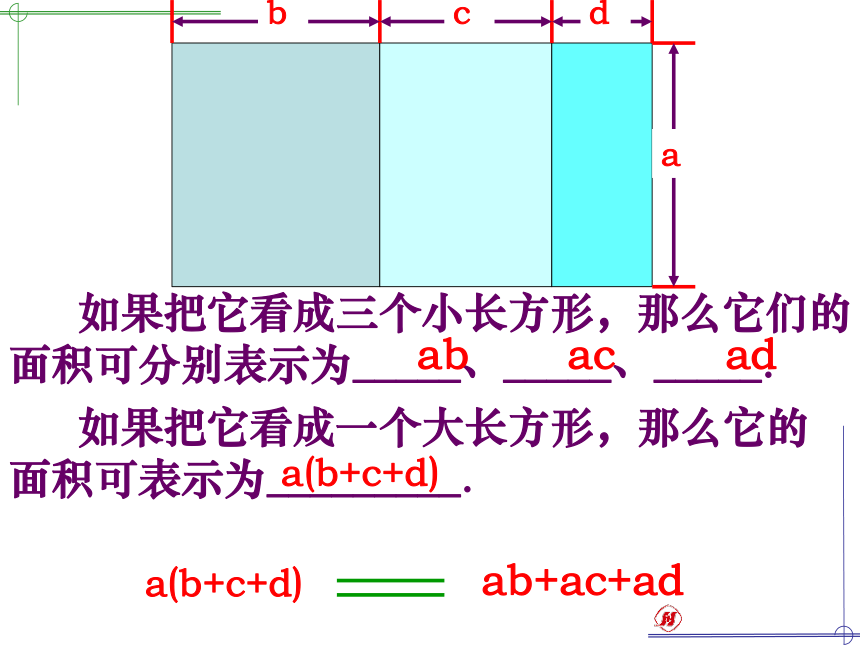
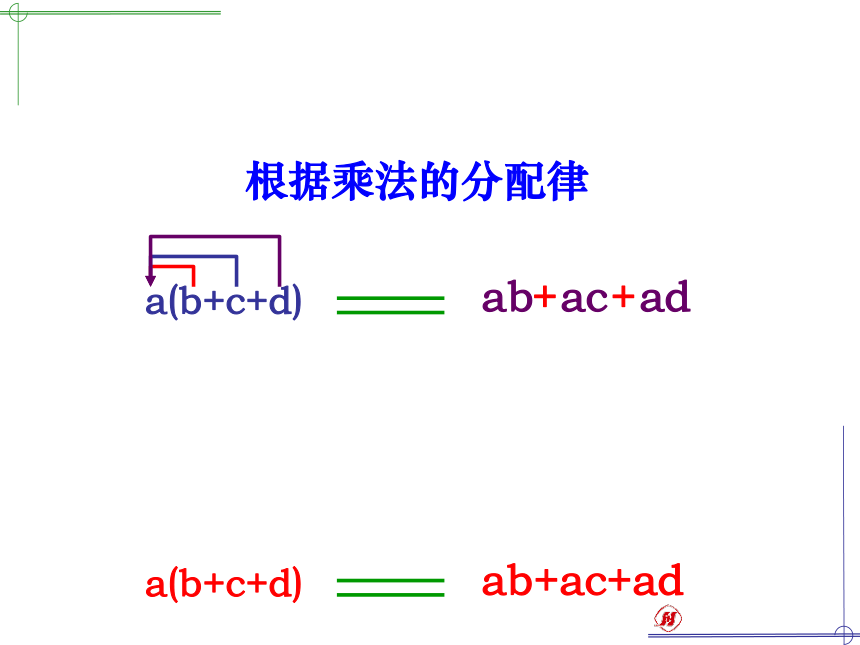
课件22张PPT。单项式乘多项式单项式乘多项式 如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____. abadac 如果把它看成一个大长方形，那么它的边长为__________,面积可表示为_________. b+c+d和aa(b+c+d) 如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____. 如果把它看成一个大长方形，那么它的面积可表示为_________. a(b+c+d)ab+ac+ada(b+c+d)a(b+c+d)ac+adab+根据乘法的分配律 单项式与多项式相乘，就是依据乘法分配律，用单项式乘多项式的每一项，再把所得的积相加.单项式乘多项式的运算法则 单项式与多项式相乘，就是依据乘法分配律，用单项式乘多项式的每一项，再把所得的积相加.例1 计算：
⑴ (-3a) ·(-2a2-3a-2)解：(-3a) ·(-2a2-3a-2)
＝(-3a) ·(-2a2)+(-3a) ·(-3a)+(-3a) ·(-2)
＝6a3+9a2+6a乘法分配率单项式乘单项式运算法则计算：
⑴ a (2a-3) ⑵ a2 (1-3a) ⑶ 3x(x2-2x-1) ⑷ -2x2y(3x2-2x-3)
(5)(2x2-3xy+4y2)(-2xy)
(6)例2：如图：一块长方形地用来建造住宅、广场、商厦，求这块地的面积.解：长方形的长为(3a+2b)+(2a-b),宽为4a,这块地的面积为：4a[(3a+2b)+(2a-b)]
＝4a(5a+b)
＝4a·5a+4a·b
=20a2+4ab
答：这块地的面积为20a2+4ab.课本第72页练习计算：
⑴ 3x(x2-2x-1)-2x2(x-3) ⑵ -6xy(x2-2xy-y2)+3xy(2x2-4xy+y2) ⑶ x2-2x[2x2-3(x2-2x-3)] ⑷ 2a(a2-3a-4)-a(2a2+6a-1)解方程：
⑴ 2x(x-1)-x(3x+2)=-x(x+2)-12 ⑵x2(3x+5)＋5=x(-x2+4x2+5x)+x已知：xy2=-6,求-xy(x3y7-3x2y5-y)计算：3x3x2x2x2x+5求图中物体的体积.若a=2,b=5,m=3,n=4,分别求下列各式的值：
(a+b)(m+n)
a(m+n)+b(m+n)
am+an+bm+bn
从上面的计算中你发现什么？再找一组看看你能从图中得到这个结论吗？这节课，我的收获是---小结与回顾布置作业课本73页
习题1、 2、3