八年级数学下册试题 19.2 平行四边形-沪科版(2课时、含答案)
文档属性
| 名称 | 八年级数学下册试题 19.2 平行四边形-沪科版(2课时、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 222.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 16:02:20 | ||
图片预览


文档简介
19.2 平行四边形
第1课时
一、选择题.
1.若平行四边形的两条对角线长为6 cm和16 cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm B.8cm C.12cm D.16cm
2.如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,测量得MN=8米,则A、B两点间的距离为( )
A.4米 B.24米 C.16米 D.48米
3.平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为( )
A.4cm,4cm,8cm,8cm
B.5cm,5cm,7cm,7cm
C.5.5cm,5.5cm,6.5cm,6.5cm
D.3cm,3cm,9cm,9cm
4.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是( )
A.60 B.30 C.20 D.16
5.如图,在Rt△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为( )
A.3 B.4 C.5 D.6
6.已知:点D,E分别是△ABC的边AB,AC的中点,如图所示.
求证:DE∥BC,且DE=BC.
证明:延长DE到点F,使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程:
①∴DFBC;
②∴CFAD.即CFBD;
③∴四边形DBCF是平行四边形;
④∴DE∥BC,且DE=BC.
则正确的证明顺序应是:( )
②→③→①→④ B.②→①→③→④
C.①→③→④→② D.①→③→②→④
二、填空题
7.在平行四边形ABCD中,∠A与∠B的度数之比为2:1,则∠C= .
8.请你从下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC中任选两个,使它们能判定四边形ABCD是平行四边形.共有 种情况符合要求.
9.如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=48m,则AB的长是 m.
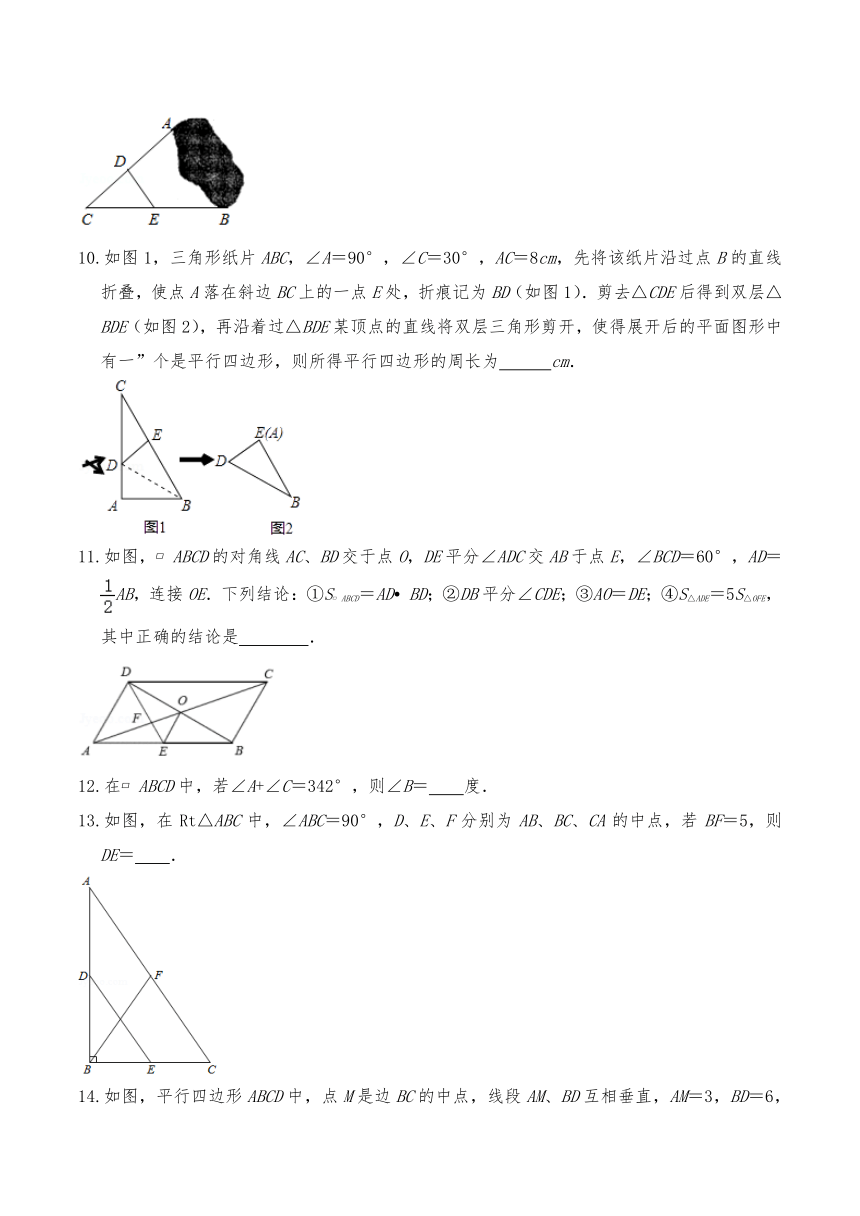
10.如图1,三角形纸片ABC,∠A=90°,∠C=30°,AC=8cm,先将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1).剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一”个是平行四边形,则所得平行四边形的周长为 cm.
11.如图, ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=AB,连接OE.下列结论:①S ABCD=AD BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的结论是 .
12.在 ABCD中,若∠A+∠C=342°,则∠B= 度.
13.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE= .
14.如图,平行四边形ABCD中,点M是边BC的中点,线段AM、BD互相垂直,AM=3,BD=6,则该平行四边形的面积为 .
三、解答题
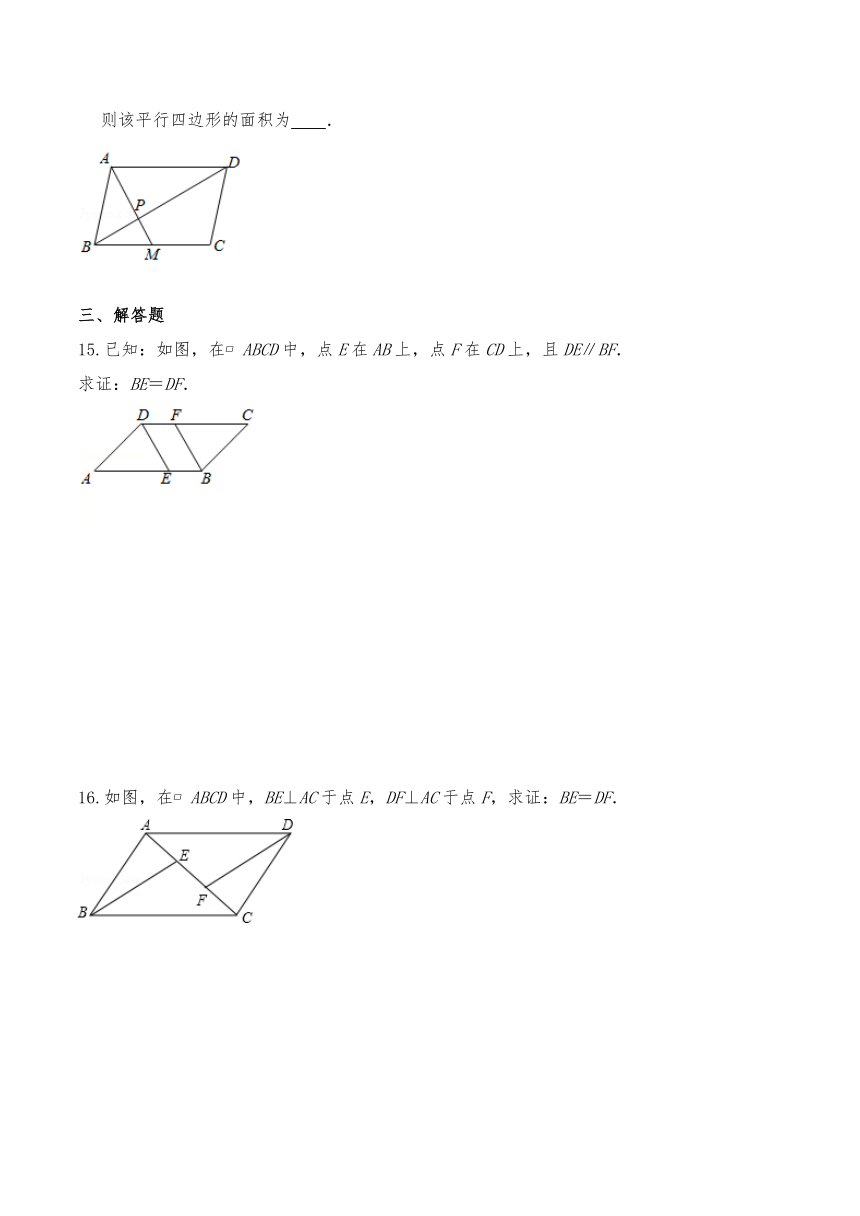
15.已知:如图,在 ABCD中,点E在AB上,点F在CD上,且DE∥BF.
求证:BE=DF.
16.如图,在 ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
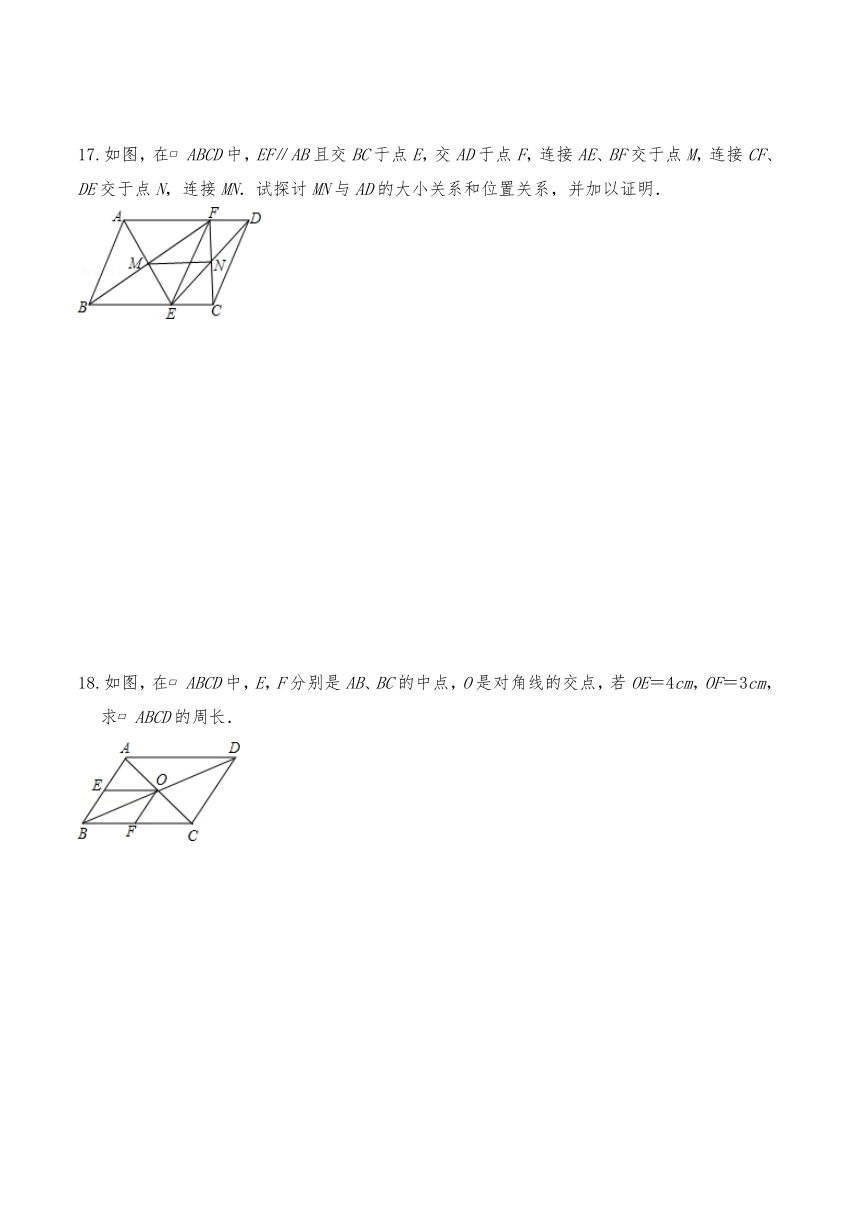
17.如图,在 ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE、BF交于点M,连接CF、DE交于点N,连接MN.试探讨MN与AD的大小关系和位置关系,并加以证明.
18.如图,在 ABCD中,E,F分别是AB、BC的中点,O是对角线的交点,若OE=4cm,OF=3cm,求 ABCD的周长.
19.如图,△ABC中,AH⊥BC于点H,点D,E分别是AB,AC的中点,连接DH,EH,DE.
(1)求证:AD=DH;
(2)若四边形ADHE的周长是30,△ADE的周长是21,求BC的长.
20.在 ABCD中,E,F分别为对角线BD上两点,连接AE,AF,CE,CF,并且AE∥CF.
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,若2BE=3EF,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ABD面积的.
第2课时
一、选择题.
1.已知 ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
2. ABCD的对角线AC、BD相交于O,AC=4,BD=5,BC=3,则△BOC的周长为( )
A.7.5 B.12 C.6 D.无法确定
3.如图,为测量池塘边A,B两点的距离,小明在池塘的一侧选取一点O,测得OA,OB的中点分别是点C、点D且CD=12米.则A,B间的距离是( )
A.24米 B.26米 C.28米 D.30米
4.如图,在 ABCD中,点E在BC上,且CD=CE,连接DE,过点A作AF⊥DE,垂足为F,若∠DAF=48°,则∠C的度数为( )
A.84° B.96° C.98° D.106°
5.如图,在 ABCD,BD为对角线,E、F分别是AD、BD的中点,连接EF,若EF=6,则CD的长是( )
A.2 B.3 C.6 D.12
6.如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
二、填空题
7.在 ABCD中,若∠B+∠D=260°,则∠A的大小为 (度).
8.如图,将平行四边形OABC放置在平面直角坐标系xOy中,O为坐标原点,若点C的坐标是(1,3),点A的坐标是(5,0),则点B的坐标是 .
9.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD= cm.
10.如图,△ABC中,BC边上的中线AD将∠BAC分成了两角∠BAD、∠DAC分别为70°和40°,若中线AD长为2.4cm,则AC长为 cm.
11.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=2,CF=3,则CD= .
12.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
13.如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是 .
14.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,且AB=PC,∠PBC=2∠PCB,则∠A= °.
三、解答题
15.如图,在 ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.
16.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.
17.如图,平行四边形ABCD的对角线AC、BD相交于点O、E、F是AC上的两点,且BF∥DE.
(1)求证:△BFO≌△DEO;
(2)求证:四边形BFDE是平行四边形.
18.如图,在四边形ABCD中,连接AC,BD交于点O,∠ADO=∠CBO,且AO=CO,E为线段OC上一点,连接DE并延长交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)若∠ADE=45°,AD⊥AC,AE=3,CE=2,求三角形AOD的面积.
19.如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
求证:(1)△AEF≌△DEC;
(2)四边形ACDF是平行四边形.
20.如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
第1课时答案
一、选择题.
B.C.B.C.B.A.
二、填空题
7. 120°. 8.4. 9.96.10.cm或cm.
11.①②. 12.9. 13.5. 14.12.
三、解答题
15.证明:∵四边形ABCD是平行四边形,
∴DC∥BA,
∴DF∥BE,
又∵DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
16.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE.
又∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AFD=∠CEB=90°,
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),
∴BE=DF.
17.解:MN=AD,MN∥AD;
证明:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵EF∥AB∴EF∥CD
∴四边形ABEF、四边形EFDC均是平行四边形,
∴AM=EM,FN=CN,
∴MN是△AED的中位线,
18.解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=CD,AD=BC,
∵E,F分别是AB、BC的中点,
∴BC=2EO,CD=2FO,
∵OE=4cm,OF=3cm,
∴BC=8cm,DC=6cm,
∴AD=8cm,AB=6cm,
∴ ABCD的周长为6+6+8+8=28(cm).
19.解:(1)∵AH⊥BC,
∴∠AHB=90°,
∵点D是AB的中点,
∴AD=DH=AB;
(2)∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∵点D,E分别是AB,AC的中点,
∴AD=DH=AB,AE=HE=AC,
∵四边形ADHE的周长是30,
∴AD+AE=×30=15,
∵△ADE的周长是21,
∴DE=21﹣15=6,
∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=12.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
∵AE∥CF,
∴∠AEF=∠CFE,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形;
(2)解:△ABE、△CDF、△BCE、△ADF,理由如下:
由(1)得:△ABE≌△CDF,
∴BE=DF,
∵2BE=3EF,
∴BE:BD=3:8,
∴△ABE的面积=△CDF的面积=△BCE的面积=△ADF的面积=△ABD面积的.
第2课时答案
一、选择题
B.A.A.B.D.D.
二、填空题
7. 50. 8.(6,3). 9.4. 10.2.4. 11..12.120°.
13.互相平分. 14.60°.
三、解答题
15.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
16.解:如图,延长BD与AC相交于点F,
∵AD平分∠BAC,BD⊥AD,
∴∠DAB=∠DAF,AD=AD,∠ADB=∠ADF,
∴△ADB≌△ADF,
∴AF=AB,BD=DF,
∵AB=6,AC=10,
∴CF=AC﹣AF=AC﹣AB=10﹣6=4,
∵E为BC中点,
∴DE是△BCF的中位线,
∴DE=CF=×4=2.
17.解:(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF∥DE,
∴∠OFB=∠OED,
在△BFO和△DEO中,
,
∴△BFO≌△DEO(AAS);
(2)证明:∵△BFO≌△DEO,
∴OE=OF,
又OB=OD,
∴四边形BFDE是平行四边形.
18.解:(1)∵AC,BD交于点O,
∴∠AOD=∠COB,
在△AOD和△COB中,
,
∴△AOD≌△COB(AAS),
∴AD=BC,
∵∠ADO=∠CBO,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)∵∠ADE=45°,AD⊥AC,
∴∠AED=45°,
∴AD=AE=3,
又∵CE=2,
∴AC=3+2=5,
∴平行四边形ABCD中,AO=AC=,
∴Rt△AOD的面积=×AD×AO=×3×=.
19.解:(1)∵在平行四边形ABCD中,AB∥CD,
∴∠FAE=∠CDE,
∵点E是边AD的中点,
∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(ASA);
(2)∵△AEF≌△DEC,
∴AF=DC,
∵AF∥DC,
∴四边形ACDF是平行四边形.
20.解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠ECF
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE.
(2)结论:CH⊥DG.理由如下:
∵△ABE≌△FCE,
∴AB=CF,
∵AB=CD,
∴DC=CF,
∵H为DG的中点,
∴CH∥FG
∵DG⊥AE,
∴CH⊥DG.
第1课时
一、选择题.
1.若平行四边形的两条对角线长为6 cm和16 cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm B.8cm C.12cm D.16cm
2.如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,测量得MN=8米,则A、B两点间的距离为( )
A.4米 B.24米 C.16米 D.48米
3.平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为( )
A.4cm,4cm,8cm,8cm
B.5cm,5cm,7cm,7cm
C.5.5cm,5.5cm,6.5cm,6.5cm
D.3cm,3cm,9cm,9cm
4.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是( )
A.60 B.30 C.20 D.16
5.如图,在Rt△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为( )
A.3 B.4 C.5 D.6
6.已知:点D,E分别是△ABC的边AB,AC的中点,如图所示.
求证:DE∥BC,且DE=BC.
证明:延长DE到点F,使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程:
①∴DFBC;
②∴CFAD.即CFBD;
③∴四边形DBCF是平行四边形;
④∴DE∥BC,且DE=BC.
则正确的证明顺序应是:( )
②→③→①→④ B.②→①→③→④
C.①→③→④→② D.①→③→②→④
二、填空题
7.在平行四边形ABCD中,∠A与∠B的度数之比为2:1,则∠C= .
8.请你从下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC中任选两个,使它们能判定四边形ABCD是平行四边形.共有 种情况符合要求.
9.如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=48m,则AB的长是 m.
10.如图1,三角形纸片ABC,∠A=90°,∠C=30°,AC=8cm,先将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1).剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一”个是平行四边形,则所得平行四边形的周长为 cm.
11.如图, ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=AB,连接OE.下列结论:①S ABCD=AD BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的结论是 .
12.在 ABCD中,若∠A+∠C=342°,则∠B= 度.
13.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE= .
14.如图,平行四边形ABCD中,点M是边BC的中点,线段AM、BD互相垂直,AM=3,BD=6,则该平行四边形的面积为 .
三、解答题
15.已知:如图,在 ABCD中,点E在AB上,点F在CD上,且DE∥BF.
求证:BE=DF.
16.如图,在 ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
17.如图,在 ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE、BF交于点M,连接CF、DE交于点N,连接MN.试探讨MN与AD的大小关系和位置关系,并加以证明.
18.如图,在 ABCD中,E,F分别是AB、BC的中点,O是对角线的交点,若OE=4cm,OF=3cm,求 ABCD的周长.
19.如图,△ABC中,AH⊥BC于点H,点D,E分别是AB,AC的中点,连接DH,EH,DE.
(1)求证:AD=DH;
(2)若四边形ADHE的周长是30,△ADE的周长是21,求BC的长.
20.在 ABCD中,E,F分别为对角线BD上两点,连接AE,AF,CE,CF,并且AE∥CF.
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,若2BE=3EF,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ABD面积的.
第2课时
一、选择题.
1.已知 ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
2. ABCD的对角线AC、BD相交于O,AC=4,BD=5,BC=3,则△BOC的周长为( )
A.7.5 B.12 C.6 D.无法确定
3.如图,为测量池塘边A,B两点的距离,小明在池塘的一侧选取一点O,测得OA,OB的中点分别是点C、点D且CD=12米.则A,B间的距离是( )
A.24米 B.26米 C.28米 D.30米
4.如图,在 ABCD中,点E在BC上,且CD=CE,连接DE,过点A作AF⊥DE,垂足为F,若∠DAF=48°,则∠C的度数为( )
A.84° B.96° C.98° D.106°
5.如图,在 ABCD,BD为对角线,E、F分别是AD、BD的中点,连接EF,若EF=6,则CD的长是( )
A.2 B.3 C.6 D.12
6.如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
二、填空题
7.在 ABCD中,若∠B+∠D=260°,则∠A的大小为 (度).
8.如图,将平行四边形OABC放置在平面直角坐标系xOy中,O为坐标原点,若点C的坐标是(1,3),点A的坐标是(5,0),则点B的坐标是 .
9.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD= cm.
10.如图,△ABC中,BC边上的中线AD将∠BAC分成了两角∠BAD、∠DAC分别为70°和40°,若中线AD长为2.4cm,则AC长为 cm.
11.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=2,CF=3,则CD= .
12.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
13.如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是 .
14.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,且AB=PC,∠PBC=2∠PCB,则∠A= °.
三、解答题
15.如图,在 ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.
16.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.
17.如图,平行四边形ABCD的对角线AC、BD相交于点O、E、F是AC上的两点,且BF∥DE.
(1)求证:△BFO≌△DEO;
(2)求证:四边形BFDE是平行四边形.
18.如图,在四边形ABCD中,连接AC,BD交于点O,∠ADO=∠CBO,且AO=CO,E为线段OC上一点,连接DE并延长交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)若∠ADE=45°,AD⊥AC,AE=3,CE=2,求三角形AOD的面积.
19.如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
求证:(1)△AEF≌△DEC;
(2)四边形ACDF是平行四边形.
20.如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
第1课时答案
一、选择题.
B.C.B.C.B.A.
二、填空题
7. 120°. 8.4. 9.96.10.cm或cm.
11.①②. 12.9. 13.5. 14.12.
三、解答题
15.证明:∵四边形ABCD是平行四边形,
∴DC∥BA,
∴DF∥BE,
又∵DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
16.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE.
又∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AFD=∠CEB=90°,
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),
∴BE=DF.
17.解:MN=AD,MN∥AD;
证明:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵EF∥AB∴EF∥CD
∴四边形ABEF、四边形EFDC均是平行四边形,
∴AM=EM,FN=CN,
∴MN是△AED的中位线,
18.解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=CD,AD=BC,
∵E,F分别是AB、BC的中点,
∴BC=2EO,CD=2FO,
∵OE=4cm,OF=3cm,
∴BC=8cm,DC=6cm,
∴AD=8cm,AB=6cm,
∴ ABCD的周长为6+6+8+8=28(cm).
19.解:(1)∵AH⊥BC,
∴∠AHB=90°,
∵点D是AB的中点,
∴AD=DH=AB;
(2)∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∵点D,E分别是AB,AC的中点,
∴AD=DH=AB,AE=HE=AC,
∵四边形ADHE的周长是30,
∴AD+AE=×30=15,
∵△ADE的周长是21,
∴DE=21﹣15=6,
∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=12.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
∵AE∥CF,
∴∠AEF=∠CFE,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形;
(2)解:△ABE、△CDF、△BCE、△ADF,理由如下:
由(1)得:△ABE≌△CDF,
∴BE=DF,
∵2BE=3EF,
∴BE:BD=3:8,
∴△ABE的面积=△CDF的面积=△BCE的面积=△ADF的面积=△ABD面积的.
第2课时答案
一、选择题
B.A.A.B.D.D.
二、填空题
7. 50. 8.(6,3). 9.4. 10.2.4. 11..12.120°.
13.互相平分. 14.60°.
三、解答题
15.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
16.解:如图,延长BD与AC相交于点F,
∵AD平分∠BAC,BD⊥AD,
∴∠DAB=∠DAF,AD=AD,∠ADB=∠ADF,
∴△ADB≌△ADF,
∴AF=AB,BD=DF,
∵AB=6,AC=10,
∴CF=AC﹣AF=AC﹣AB=10﹣6=4,
∵E为BC中点,
∴DE是△BCF的中位线,
∴DE=CF=×4=2.
17.解:(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF∥DE,
∴∠OFB=∠OED,
在△BFO和△DEO中,
,
∴△BFO≌△DEO(AAS);
(2)证明:∵△BFO≌△DEO,
∴OE=OF,
又OB=OD,
∴四边形BFDE是平行四边形.
18.解:(1)∵AC,BD交于点O,
∴∠AOD=∠COB,
在△AOD和△COB中,
,
∴△AOD≌△COB(AAS),
∴AD=BC,
∵∠ADO=∠CBO,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)∵∠ADE=45°,AD⊥AC,
∴∠AED=45°,
∴AD=AE=3,
又∵CE=2,
∴AC=3+2=5,
∴平行四边形ABCD中,AO=AC=,
∴Rt△AOD的面积=×AD×AO=×3×=.
19.解:(1)∵在平行四边形ABCD中,AB∥CD,
∴∠FAE=∠CDE,
∵点E是边AD的中点,
∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(ASA);
(2)∵△AEF≌△DEC,
∴AF=DC,
∵AF∥DC,
∴四边形ACDF是平行四边形.
20.解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠ECF
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE.
(2)结论:CH⊥DG.理由如下:
∵△ABE≌△FCE,
∴AB=CF,
∵AB=CD,
∴DC=CF,
∵H为DG的中点,
∴CH∥FG
∵DG⊥AE,
∴CH⊥DG.
