数学人教A版(2019)必修第二册8.5.1直线与直线平行 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.5.1直线与直线平行 课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 18:14:23 | ||
图片预览




文档简介
(共17张PPT)
利用课前时间,了解一下莘县的地标建筑——雁塔吧。雁塔习称“燕塔”,位于莘县城内,为楼阁式十三层平面八角型砖塔,塔底层东西长23米,南北长22米,高40多米。塔有四门,入北门可攀至顶部,南门内有一尊石雕女神像。塔内藏有五部北宋刻本《妙法莲花经》,一部写本《陀罗尼经》,一个精致的小银塔和一具石函(棺)。小银塔用银质薄片砸合而成,造型优美,玲珑剔透。石函内有水,水上漂浮着银质薄片船,水内有舍利子。巍峨雄伟的雁塔,历史上多被用作军事瞭望台。
今天积极主动的同学,等疫情之后,我们一起去登雁塔!
当你漫步在雁塔广场时,你会看到很多的灯杆,请思考:
灯杆所在直线满足怎样的位置关系呢?
当你漫步在雁塔广场时,你会看到很多的灯杆,请思考:
灯杆所在直线满足怎样的位置关系呢?
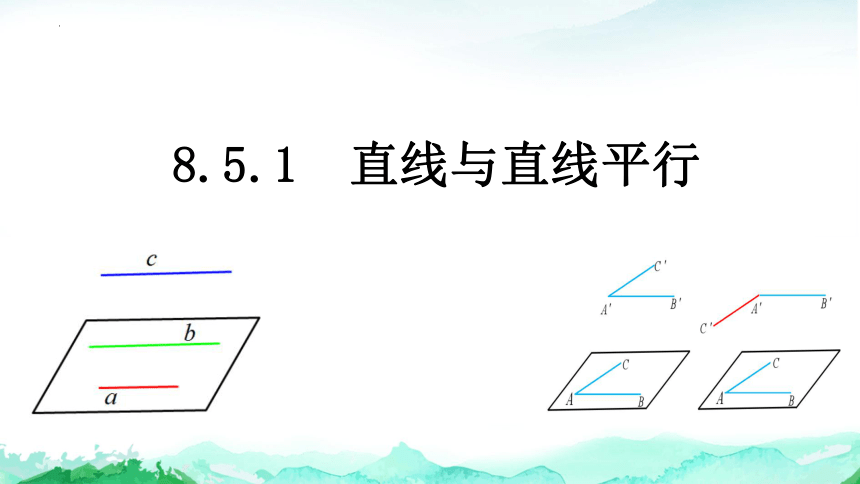
8.5.1 直线与直线平行
学习目标 核心素养
1.探究并掌握基本事实4; 2.探究并证明“等角定理”; 3.结合基本事实4和“等角定理”的探究,体会平面图形结论在空间图形中的推广,体会研究几何问题的一般方法. 在学习和应用基本事实4和定理的过程中,通过判断和证明空间两条直线的位置关系,发展数学抽象素养、逻辑推理素养和直观想象素养.
重点:平行线的传递性和“等角定理”的探究及应用.难点:空间等角定理的证明.
(1)在同一平面内,如果两条直线都和第三条
直线平行,则这两条直线平行.( )
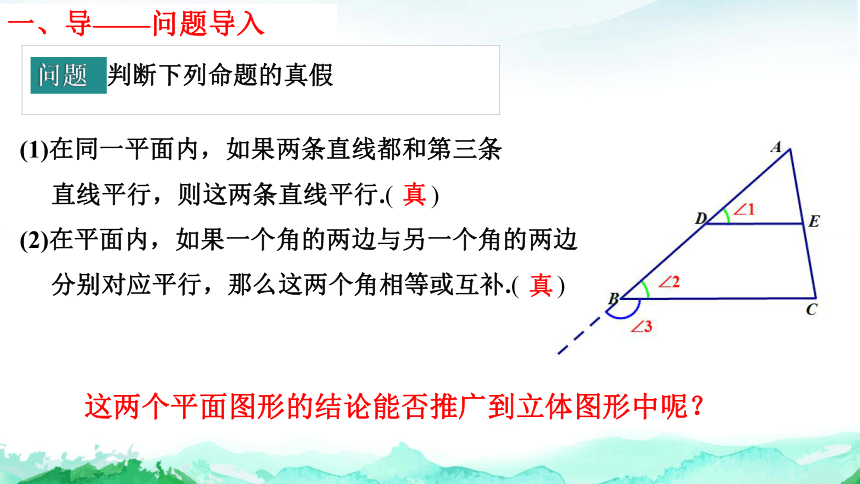
(2)在平面内,如果一个角的两边与另一个角的两边
分别对应平行,那么这两个角相等或互补.( )
一、导——问题导入
真
真
这两个平面图形的结论能否推广到立体图形中呢?
问题
判断下列命题的真假
在长方体ABCD- A′B′C′D′中,
DC//AB,A′B′//AB.DC与A′B′平行吗?
观察你所在的教室,你能找到类似的实例吗?
动手实验
把一张长方形的纸对折几次,打开,观察折痕,这些折痕之间有什么关系?
观察
a
b
c
一、导——探究基本事实4
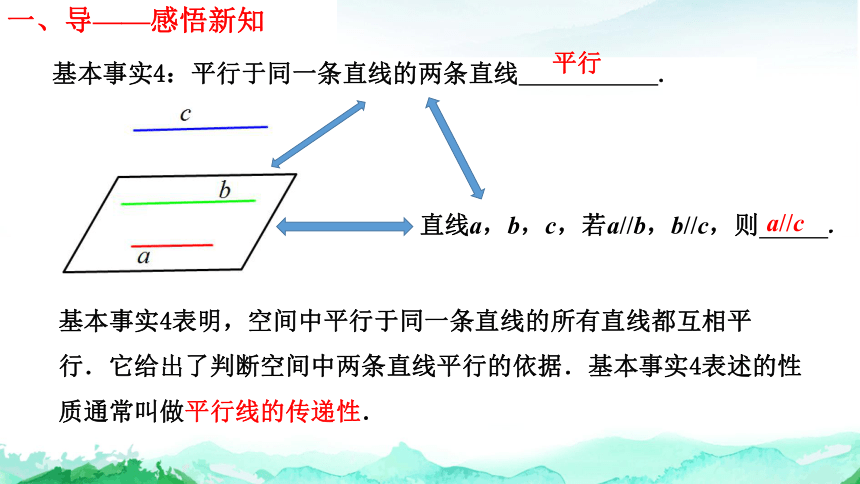
直线a,b,c,若a//b,b//c,则 .
基本事实4:平行于同一条直线的两条直线 .
平行
a//c
基本事实4表明,空间中平行于同一条直线的所有直线都互相平行.它给出了判断空间中两条直线平行的依据.基本事实4表述的性质通常叫做平行线的传递性.
一、导——感悟新知
一、导——探究“等角定理”
与平面中的情况类似,当空间中两个角的两条边分别对应平行时,这两个角有如图所示的两种位置.
在平面内,如果一个角的两边与另一个角的两边分别对应平行,那么这两个角相等或互补.在空间中,这一结论是否仍然成立呢?
(1)
(2)
二、思——任务驱动,独立思考
【阅读课本】第134-135页,理清证明思路,研习证明的规范表达,并完成如下任务:
(1)证明 的方法是什么?
(2)试着写出图(2)的证明过程.
(2)
三、议——思维碰撞,合作提升
四、展——分享成果,展示自我
1.核对例1的规范解答过程、变式1和变式2的结论,总结出证明直线平行的方法;
2.寻求图(2)的证明方法,总结出证明角相等的方法.
1.板演:例1;
2.口答:变式1、变式2;
3.展台展示:图(2)的证明思路.
(2)
五、评——解决问题,形成共识
全等三角形(SSS)
基本事实4
五、评——解决问题,形成共识
(2)
说明:等角定理实质上是由以下两个结论合成的:
①若一个角的两边与另一个角的两边分别平行且方向都相同(或方向都相反),则这两个角相等;
②若一个角的两边与另一个角的两边分别平行,有一组对应边方向相同,另一组对应边方向相反,则这两个角互补.
等角定理 如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
五、评——解决问题,形成共识
思考:基本事实4和“等角定理”都是由平面图形推广到立体图形得到的.是不是所有关于平面图形的结论都可以推广到立体图形呢?
比如“平面内,垂直于同一条直线的两条直线平行”
五、评——小结
2.空间“等角定理”的内容是什么?我们是如何探究的?
在证明的过程中有什么注意事项?
3.你还能举出一些平面内的结论推广至空间中依然成立的结论吗?
通过对典型实例观察、动手实验,
然后猜想、概括得出结论.
在类比平面图形等角定理的基础上进行了演绎推理和逻辑论证.这种直观感知、操作确认、思辨论证的研究问题模式在后面的学习过程中将不断重现.
过直线外一点有且只有一条直线与已知直线平行.
注意证明过程严谨性,必要时分类讨论.
研究几何问题的一般方法
1.基本事实4的内容是什么?我们是如何探究的?
(六)检:限时检测,反馈效果
作业:课本135页,第3题、4题.
谢谢大家,再见!
利用课前时间,了解一下莘县的地标建筑——雁塔吧。雁塔习称“燕塔”,位于莘县城内,为楼阁式十三层平面八角型砖塔,塔底层东西长23米,南北长22米,高40多米。塔有四门,入北门可攀至顶部,南门内有一尊石雕女神像。塔内藏有五部北宋刻本《妙法莲花经》,一部写本《陀罗尼经》,一个精致的小银塔和一具石函(棺)。小银塔用银质薄片砸合而成,造型优美,玲珑剔透。石函内有水,水上漂浮着银质薄片船,水内有舍利子。巍峨雄伟的雁塔,历史上多被用作军事瞭望台。
今天积极主动的同学,等疫情之后,我们一起去登雁塔!
当你漫步在雁塔广场时,你会看到很多的灯杆,请思考:
灯杆所在直线满足怎样的位置关系呢?
当你漫步在雁塔广场时,你会看到很多的灯杆,请思考:
灯杆所在直线满足怎样的位置关系呢?
8.5.1 直线与直线平行
学习目标 核心素养
1.探究并掌握基本事实4; 2.探究并证明“等角定理”; 3.结合基本事实4和“等角定理”的探究,体会平面图形结论在空间图形中的推广,体会研究几何问题的一般方法. 在学习和应用基本事实4和定理的过程中,通过判断和证明空间两条直线的位置关系,发展数学抽象素养、逻辑推理素养和直观想象素养.
重点:平行线的传递性和“等角定理”的探究及应用.难点:空间等角定理的证明.
(1)在同一平面内,如果两条直线都和第三条
直线平行,则这两条直线平行.( )
(2)在平面内,如果一个角的两边与另一个角的两边
分别对应平行,那么这两个角相等或互补.( )
一、导——问题导入
真
真
这两个平面图形的结论能否推广到立体图形中呢?
问题
判断下列命题的真假
在长方体ABCD- A′B′C′D′中,
DC//AB,A′B′//AB.DC与A′B′平行吗?
观察你所在的教室,你能找到类似的实例吗?
动手实验
把一张长方形的纸对折几次,打开,观察折痕,这些折痕之间有什么关系?
观察
a
b
c
一、导——探究基本事实4
直线a,b,c,若a//b,b//c,则 .
基本事实4:平行于同一条直线的两条直线 .
平行
a//c
基本事实4表明,空间中平行于同一条直线的所有直线都互相平行.它给出了判断空间中两条直线平行的依据.基本事实4表述的性质通常叫做平行线的传递性.
一、导——感悟新知
一、导——探究“等角定理”
与平面中的情况类似,当空间中两个角的两条边分别对应平行时,这两个角有如图所示的两种位置.
在平面内,如果一个角的两边与另一个角的两边分别对应平行,那么这两个角相等或互补.在空间中,这一结论是否仍然成立呢?
(1)
(2)
二、思——任务驱动,独立思考
【阅读课本】第134-135页,理清证明思路,研习证明的规范表达,并完成如下任务:
(1)证明 的方法是什么?
(2)试着写出图(2)的证明过程.
(2)
三、议——思维碰撞,合作提升
四、展——分享成果,展示自我
1.核对例1的规范解答过程、变式1和变式2的结论,总结出证明直线平行的方法;
2.寻求图(2)的证明方法,总结出证明角相等的方法.
1.板演:例1;
2.口答:变式1、变式2;
3.展台展示:图(2)的证明思路.
(2)
五、评——解决问题,形成共识
全等三角形(SSS)
基本事实4
五、评——解决问题,形成共识
(2)
说明:等角定理实质上是由以下两个结论合成的:
①若一个角的两边与另一个角的两边分别平行且方向都相同(或方向都相反),则这两个角相等;
②若一个角的两边与另一个角的两边分别平行,有一组对应边方向相同,另一组对应边方向相反,则这两个角互补.
等角定理 如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
五、评——解决问题,形成共识
思考:基本事实4和“等角定理”都是由平面图形推广到立体图形得到的.是不是所有关于平面图形的结论都可以推广到立体图形呢?
比如“平面内,垂直于同一条直线的两条直线平行”
五、评——小结
2.空间“等角定理”的内容是什么?我们是如何探究的?
在证明的过程中有什么注意事项?
3.你还能举出一些平面内的结论推广至空间中依然成立的结论吗?
通过对典型实例观察、动手实验,
然后猜想、概括得出结论.
在类比平面图形等角定理的基础上进行了演绎推理和逻辑论证.这种直观感知、操作确认、思辨论证的研究问题模式在后面的学习过程中将不断重现.
过直线外一点有且只有一条直线与已知直线平行.
注意证明过程严谨性,必要时分类讨论.
研究几何问题的一般方法
1.基本事实4的内容是什么?我们是如何探究的?
(六)检:限时检测,反馈效果
作业:课本135页,第3题、4题.
谢谢大家,再见!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
