2023年初中数学中考备考必刷题: 解直角三角形考点冲刺练(含答案)
文档属性
| 名称 | 2023年初中数学中考备考必刷题: 解直角三角形考点冲刺练(含答案) | 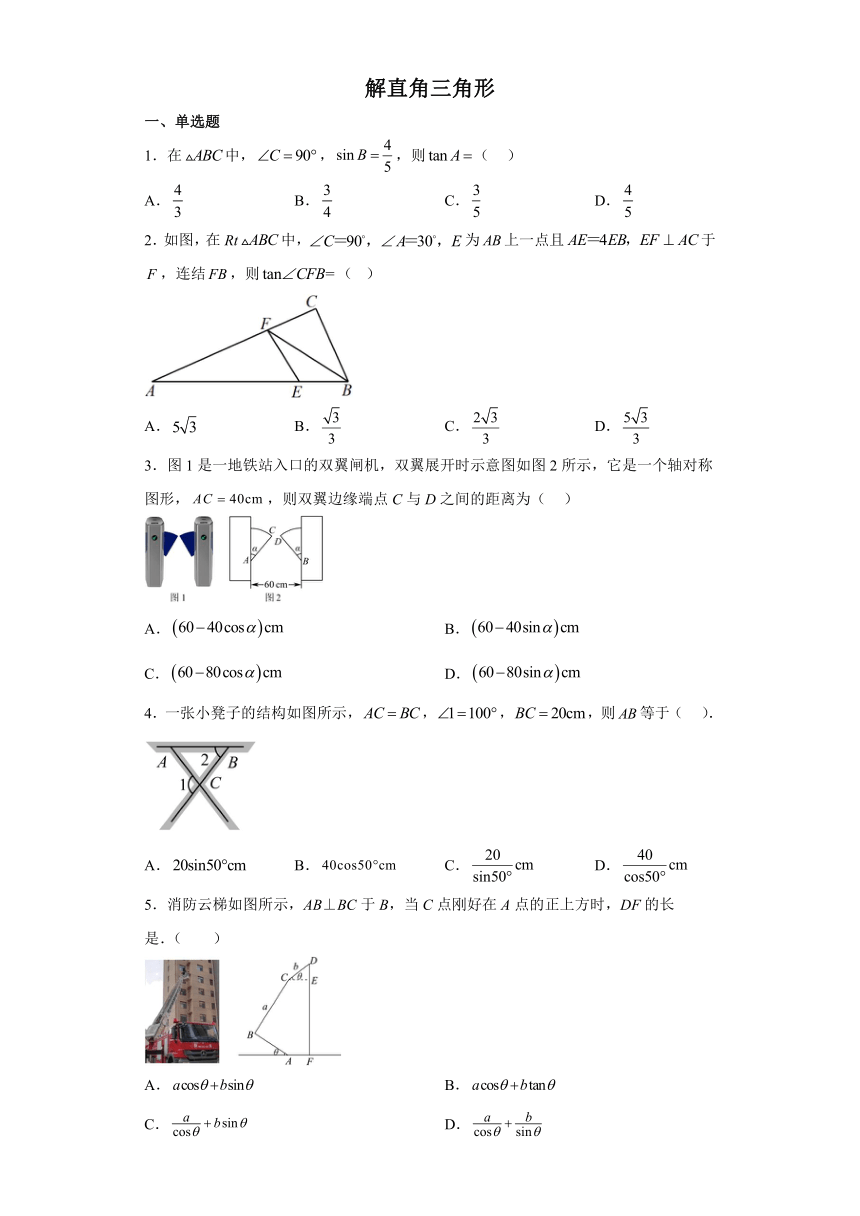 | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 18:58:31 | ||
图片预览





文档简介
解直角三角形
一、单选题
1.在中,,,则( )
A. B. C. D.
2.如图,在Rt中,为上一点且于,连结,则( )
A. B. C. D.
3.图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,,则双翼边缘端点C与D之间的距离为( )
A. B.
C. D.
4.一张小凳子的结构如图所示,,,,则等于( ).
A. B. C. D.
5.消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是.( )
A. B.
C. D.
6.如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
7.如图为一节楼梯的示意图,,,米.现要在楼梯上铺一块地毯,楼梯宽度为1米.则地毯的面积至少需要( )平方米.
A. B. C. D.
8.在中,,则的长为( )
A. B. C. D.
二、填空题
9.在中,,,,则__________.
10.如图,一辆小车沿倾斜角为的斜坡向上行驶26米,已知,则小车上升的高度是________米.
11.图1是一款摆臂遮阳蓬的实物图,图2是其侧面示意图,点A,O为墙壁上的固定点,摆臂OB绕点O旋转过程中,遮阳蓬AB可自由伸缩,蓬面始终保持平整.如图2,米,光线l与水平地面的夹角为,此时身高为1米的小朋友(米)站在遮阳蓬下距离墙角1.2米(米)处,刚好不被阳光照射到,此时小朋友的头顶M距离遮阳蓬的竖直高度(MP)为_________米;同一时刻下,旋转摆臂OB,点B的对应点恰好位于小朋友头顶M的正上方,当小朋友后退至刚好不被阳光照射到时,其头顶距离遮阳蓬的竖直高度为_________米.
12.如图,在矩形中,点在上,点点在上,若点与点关于对称,点与点关于对称,与相交于点,则___________.
13.如图1是超市的手推车,如图2是其侧面示意图,已知前后车轮半径均为,两个车轮的圆心的连线与地面平行,测得支架,、所在直线与地面的夹角分别为、,.
(1)扶手前端到地面的距离为______;
(2)手推车内装有简易宝宝椅,为小坐板,打开后,椅子的支点到点的距离为10cm,,,,坐板的宽度为______.
14.图1是某折叠式躺椅的实物图,图2是靠背垂直地面时的侧面展开图,此时四边形ABCD是矩形,AB=20cm,AD=cm,DE=60cm,BF=30cm.点H在BC上,椅子的支撑杆AF、BG、CE分别绕B、H、D转动并带动AI转动,支撑杆LK、JM不动.躺椅在转动时:
(1)若直线EF过点J,当∠ADE=120°时,AFJ的面积是______cm2.
(2)若,EF与地面的夹角为α,则的取值范围是_____.
15.如图,在中,,,,交于点.点为线段上的动点,则的最小值为________.
16.一款闭门器按如图1所示安装,支点,分别固定在门框和门板上,门宽,摇臂,连杆,闭门器工作时,摇臂、连杆和长度均固定不变.如图2,当门闭合时,,则的长为_________cm.如图3,门板绕点旋转,当时,点到门框的距离,则的长为__________cm.
三、解答题
17.如图是置物架的侧面示意图,置物板与地面平行,斜支架与地面的夹角,;挡板与置物板的夹角,.求挡板顶端F到地面的距离.(参考数据:,,)
18.小王和小李负责某企业宣传片的制作,期间要使用无人机采集一组航拍的资料.在航拍时,小王在处测得无人机的仰角为,同时小李登上斜坡的处测得无人机的仰角为.若小李所在斜坡的坡比为:,铅垂高度米(点,,,在同一水平线上).
(1)小王和小李两人之间的距离;
(2)此时无人机的高度.(,,,结果精确到米)
19.为巩固农村脱贫成果,利兴村委会计划利用一块如图所示的空地,培育绿植销售,空地南北边界,西边界,经测量得到如下数据,点在点的北偏东方向,在点的北偏东方向,米,求空地南北边界和的长(结果保留整数,参考数据:,).
20.周末,小红和小宇相约一起去郊外劳动基地参加劳动.已知小红家在小宇家的北偏西方向上,.两人到达劳动基地处后,发现小宇家在劳动基地的南偏西方向上,小红家在劳动基地的南偏西方向上.求小宇家到劳动基地的距离.(结果保留1位小数;参考数据:,,,)
21.某商场要建一个地下停车场,下图是地下停车场的入口设计示意图,拟设计斜坡的倾斜角为,一楼到地下停车场地面的距离米,地平线到一楼的垂直距离米.
(1)为保证斜坡倾斜角为,应在地面上距点多远的处开始斜坡的施工?(精确到米)
(2)如果一辆高米的小货车要进入地下停车场,能否进入?为什么?(参考数据:,,)
22.2022年6月28日,美国“本福德”号导弹驱逐舰穿航台湾海峡并公开炒作,为了维护国家安全和祖国统一,我中国人民解放军东部战区组织海空兵力对美舰进行全程跟监警戒.一架飞机沿水平直线飞行,在点处测得正前方水平地面上某建筑物的顶端的俯角为,飞机面向方向继续飞行米至点处,测得该建筑物底端的俯角为,已知建筑物的高为米,求飞机飞行的高度.(结果精确到1米,参考数据:,)
参考答案:
1.B
解:在中,,,
设,则,
∴,
∴,
故选:B
2.D
解:设,,则AB=5x,
∵,
∴∠AFE=
∵,
∴,
∴x,
在Rt△BCF中,∠C=90,
∴.
3.D
解:如图,作直线,交双翼闸机于点E、F,则,
由题意可得,,
在直角三角形中,∵,
∴,
∴;
4.B
如图,过点C作于点D.
∵,
∴.
∵,,
∴,.
在中,,即,
∴,
∴.
5.C
解:连接CA,如图,
由题可知四边形CAF 是矩形,
∴CA⊥AF,EF=CA,
∴,
∵AB⊥BC,
∴,
∴,
在Rt△ABC中,,
∴,
在Rt△CDE中,,
∴,
∴.
6.B
解:如图,过点P作PE⊥x轴于点E.
设点P的坐标为(x,y),
则OE=x,PE=y.
在Rt△OPE中,
∵cosα= ,OP=13,
∴OE=5.
∴PE==12.
∴P点的坐标为(5,12).
7.A
解:由题意,在中,(米),
所以地毯的长度为(米),
所以地毯的面积至少需要(平方米),
8.B
解:
9.
∵在中,,,
,
∴.
故答案为:.
10.10
解:∵,
∴该直角三角形的三边之比为5∶12∶13,
∴,
∵小车沿倾斜角为的斜坡向上行驶26米,
∴小车上升的高度是米;
故答案为10.
11. 0.2 1.1
解:设MN交OB于点C,
根据题意得:OC=QN=1.2米,PC⊥OB,∠CBN=,
∴tan∠CBN=3,
∴BC=OB-OC=0.3米,
∵∠AOB=90°,OA=OB,
∴△AOB为等腰直角三角形,
∴∠PBC=45°,
∴△PBC为等腰直角三角形,
∴PC=BC=0.3米,
∵tan∠CBN=3,
∴CN=3BC=0.9米,
∵MN=1米,
∴CM=0.1米,
∴PM=0.2米;
如图,过点B′作B′F⊥AQ于点F,设小朋友后退至点D,刚好不被阳光照射到,过点D作DE⊥OB交A B′于点E,交B′F于点G,则B′D∥l,
根据题意得:B′F=QN=1.2米,FQ=DG,O B′=1.5米,OQ=CN=0.9米,,
∴米,
∴AF=OA-OF=0.6米,DG=FQ=1.8米,
∴,
∵,
∴B′G=0.6米,
∴EG=0.3米,
∴DE=2.1米,
∴头顶距离遮阳蓬的竖直高度为2.1-1=1.1米.
故答案为:0.2,1.1
12./
解:∵点与点关于对称,
∴
又∵,
∴是等腰直角三角形,
∴,
∵点点关于对称,
∴
∵,
∴,
∴,
∴,
在中,,
∴,
∴,
∴.
故答案为:.
13.
(1) 解:过D作交于G,过C作交于K,
∵、所在直线与地面的夹角分别为,
∴,,
∵,,
∴,,
∵前后车轮半径均为,
∴扶手前端到地面的距离为: ,
故答空1为 ;
(2)解:过E作交于Q,
∵,
∴,
∵,,设为x,
∴,,
由三角函数得,
,
解得:,
∴,
故答案为 ;
14.
解:若直线EF过点J,当∠ADE=120°时,如图1所示,
由题意可知,ABCD,
∴ ∠F=∠E,∠FAJ=∠ADE=120°,
∴△FAJ∽△EDJ,
∴,
∵AF=AB+BF=50cm,DE=60cm,
∴
∴AJ=AD=cm,
过点F作FN⊥DA交DA的延长线于点N,则∠ANF=90°,
在Rt△AFN中,∠FAN=180°-∠FAJ=60°,AF=50cm,
∴FN=AFsin∠FAN=50×sin60°=25,
∴AFJ的面积=×AJ×FN=cm2;
当tan∠EDI=时,如图2所示,作EP⊥DI于点P,则∠EPD=90°,设EF交AD于点Q,
由题意可知,ABCD,
∴ ∠F=∠QED,∠FAQ=∠QDE,
∴△FAQ∽△EDQ,
∴,
∵AF=AB+BF=50cm,DE=60cm,
∴
∴DQ=AD=cm,
设EP=x,则DP=2x,由勾股定理得
,
∴,
解得x=12 cm,
∴EP=12cm,DP=24cm,PQ=DP+DQ=cm,
∴=tan∠EQP=;
当tan∠EDI=2时,如图3所示,
同理可求得DQ=cm,DP=12 cm,EP=24cm,
∴PQ=DP+DQ=cm,
∴=tan∠EQP=;
∵EF与地面的夹角α随着∠EDI的增大而增大,
∴当时,的取值范围是.
故答案为:cm2;.
15.
解:过点P作PH⊥AB于点H,如图所示:
∵,,,
∴,
∴,
∴,
∴,
∴,
若使的值为最小,也就相当于为最小,
∴当点C、P、H三点共线时,的值为最小,如图所示:
∵,
∴,
∴的最小值为;
故答案为.
16.
解:过作,为垂足,
,
,
,
,
,
,
.
故答案:.
解:如图,连接,作,为垂足,为的对应点,
,
,
,
,
设,则,
,
由题空1得:,,
,
又
,
,
即:,
整理得:,
解得:,(舍去),
.
故答案:.
17.112
解:如图,过点E作于点G,过点F作,交延长线于点M,
在中,,,
由,得,
∵,
∴,
在中,由,得,
∴.
答:挡板顶端F到地面的距离为112.
18.(1)米
(2)米
(1)解:∵小李所在斜坡的坡比为:,铅垂高度米
∴(米),
∴;
(2)解:设,如图所示,过点作于点,
∴,,则,
∵,
∴,
∴,
在中,,
∴,
解得:,
∴米.
答:无人机的高度约为21米.
19.的长和的长分别约为米和米.
解:过作于于,
∵,
∴,
∵,
∴四边形为矩形,
∵,
∴在中,,
∵米,,
∴(米),
∵,
∴在中,,
∵四边形为矩形,
∴米,
∵,
∴(米),
∴(米),
答:的长和的长分别约为米和米.
20.小宇家到劳动基地的距离约为7.1km
解:如图,过点作,垂足为.
由题意,得,
.
在中,,
∴,
.
在中,,
∴.
答:小宇家到劳动基地的距离约为7.1km.
21.(1)5.6米
(2)能,理由见解析
(1)解:斜坡的倾斜角为,
,
(米),
在中,(米),
答:在地面上距点约5.6米的处开始斜坡的施工.
(2)过作,垂足为,
,
,
,
在中,(米),
,
货车能进入地下停车场.
22.飞机飞行的高度约为米
解:过作,交的延长线于,如图所示:
设米,
由题意得:米,,,
在中,,
,
在中,,
米,
米,
,
解得:,
.
答:飞机飞行的高度约为米.
一、单选题
1.在中,,,则( )
A. B. C. D.
2.如图,在Rt中,为上一点且于,连结,则( )
A. B. C. D.
3.图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,,则双翼边缘端点C与D之间的距离为( )
A. B.
C. D.
4.一张小凳子的结构如图所示,,,,则等于( ).
A. B. C. D.
5.消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是.( )
A. B.
C. D.
6.如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
7.如图为一节楼梯的示意图,,,米.现要在楼梯上铺一块地毯,楼梯宽度为1米.则地毯的面积至少需要( )平方米.
A. B. C. D.
8.在中,,则的长为( )
A. B. C. D.
二、填空题
9.在中,,,,则__________.
10.如图,一辆小车沿倾斜角为的斜坡向上行驶26米,已知,则小车上升的高度是________米.
11.图1是一款摆臂遮阳蓬的实物图,图2是其侧面示意图,点A,O为墙壁上的固定点,摆臂OB绕点O旋转过程中,遮阳蓬AB可自由伸缩,蓬面始终保持平整.如图2,米,光线l与水平地面的夹角为,此时身高为1米的小朋友(米)站在遮阳蓬下距离墙角1.2米(米)处,刚好不被阳光照射到,此时小朋友的头顶M距离遮阳蓬的竖直高度(MP)为_________米;同一时刻下,旋转摆臂OB,点B的对应点恰好位于小朋友头顶M的正上方,当小朋友后退至刚好不被阳光照射到时,其头顶距离遮阳蓬的竖直高度为_________米.
12.如图,在矩形中,点在上,点点在上,若点与点关于对称,点与点关于对称,与相交于点,则___________.
13.如图1是超市的手推车,如图2是其侧面示意图,已知前后车轮半径均为,两个车轮的圆心的连线与地面平行,测得支架,、所在直线与地面的夹角分别为、,.
(1)扶手前端到地面的距离为______;
(2)手推车内装有简易宝宝椅,为小坐板,打开后,椅子的支点到点的距离为10cm,,,,坐板的宽度为______.
14.图1是某折叠式躺椅的实物图,图2是靠背垂直地面时的侧面展开图,此时四边形ABCD是矩形,AB=20cm,AD=cm,DE=60cm,BF=30cm.点H在BC上,椅子的支撑杆AF、BG、CE分别绕B、H、D转动并带动AI转动,支撑杆LK、JM不动.躺椅在转动时:
(1)若直线EF过点J,当∠ADE=120°时,AFJ的面积是______cm2.
(2)若,EF与地面的夹角为α,则的取值范围是_____.
15.如图,在中,,,,交于点.点为线段上的动点,则的最小值为________.
16.一款闭门器按如图1所示安装,支点,分别固定在门框和门板上,门宽,摇臂,连杆,闭门器工作时,摇臂、连杆和长度均固定不变.如图2,当门闭合时,,则的长为_________cm.如图3,门板绕点旋转,当时,点到门框的距离,则的长为__________cm.
三、解答题
17.如图是置物架的侧面示意图,置物板与地面平行,斜支架与地面的夹角,;挡板与置物板的夹角,.求挡板顶端F到地面的距离.(参考数据:,,)
18.小王和小李负责某企业宣传片的制作,期间要使用无人机采集一组航拍的资料.在航拍时,小王在处测得无人机的仰角为,同时小李登上斜坡的处测得无人机的仰角为.若小李所在斜坡的坡比为:,铅垂高度米(点,,,在同一水平线上).
(1)小王和小李两人之间的距离;
(2)此时无人机的高度.(,,,结果精确到米)
19.为巩固农村脱贫成果,利兴村委会计划利用一块如图所示的空地,培育绿植销售,空地南北边界,西边界,经测量得到如下数据,点在点的北偏东方向,在点的北偏东方向,米,求空地南北边界和的长(结果保留整数,参考数据:,).
20.周末,小红和小宇相约一起去郊外劳动基地参加劳动.已知小红家在小宇家的北偏西方向上,.两人到达劳动基地处后,发现小宇家在劳动基地的南偏西方向上,小红家在劳动基地的南偏西方向上.求小宇家到劳动基地的距离.(结果保留1位小数;参考数据:,,,)
21.某商场要建一个地下停车场,下图是地下停车场的入口设计示意图,拟设计斜坡的倾斜角为,一楼到地下停车场地面的距离米,地平线到一楼的垂直距离米.
(1)为保证斜坡倾斜角为,应在地面上距点多远的处开始斜坡的施工?(精确到米)
(2)如果一辆高米的小货车要进入地下停车场,能否进入?为什么?(参考数据:,,)
22.2022年6月28日,美国“本福德”号导弹驱逐舰穿航台湾海峡并公开炒作,为了维护国家安全和祖国统一,我中国人民解放军东部战区组织海空兵力对美舰进行全程跟监警戒.一架飞机沿水平直线飞行,在点处测得正前方水平地面上某建筑物的顶端的俯角为,飞机面向方向继续飞行米至点处,测得该建筑物底端的俯角为,已知建筑物的高为米,求飞机飞行的高度.(结果精确到1米,参考数据:,)
参考答案:
1.B
解:在中,,,
设,则,
∴,
∴,
故选:B
2.D
解:设,,则AB=5x,
∵,
∴∠AFE=
∵,
∴,
∴x,
在Rt△BCF中,∠C=90,
∴.
3.D
解:如图,作直线,交双翼闸机于点E、F,则,
由题意可得,,
在直角三角形中,∵,
∴,
∴;
4.B
如图,过点C作于点D.
∵,
∴.
∵,,
∴,.
在中,,即,
∴,
∴.
5.C
解:连接CA,如图,
由题可知四边形CAF 是矩形,
∴CA⊥AF,EF=CA,
∴,
∵AB⊥BC,
∴,
∴,
在Rt△ABC中,,
∴,
在Rt△CDE中,,
∴,
∴.
6.B
解:如图,过点P作PE⊥x轴于点E.
设点P的坐标为(x,y),
则OE=x,PE=y.
在Rt△OPE中,
∵cosα= ,OP=13,
∴OE=5.
∴PE==12.
∴P点的坐标为(5,12).
7.A
解:由题意,在中,(米),
所以地毯的长度为(米),
所以地毯的面积至少需要(平方米),
8.B
解:
9.
∵在中,,,
,
∴.
故答案为:.
10.10
解:∵,
∴该直角三角形的三边之比为5∶12∶13,
∴,
∵小车沿倾斜角为的斜坡向上行驶26米,
∴小车上升的高度是米;
故答案为10.
11. 0.2 1.1
解:设MN交OB于点C,
根据题意得:OC=QN=1.2米,PC⊥OB,∠CBN=,
∴tan∠CBN=3,
∴BC=OB-OC=0.3米,
∵∠AOB=90°,OA=OB,
∴△AOB为等腰直角三角形,
∴∠PBC=45°,
∴△PBC为等腰直角三角形,
∴PC=BC=0.3米,
∵tan∠CBN=3,
∴CN=3BC=0.9米,
∵MN=1米,
∴CM=0.1米,
∴PM=0.2米;
如图,过点B′作B′F⊥AQ于点F,设小朋友后退至点D,刚好不被阳光照射到,过点D作DE⊥OB交A B′于点E,交B′F于点G,则B′D∥l,
根据题意得:B′F=QN=1.2米,FQ=DG,O B′=1.5米,OQ=CN=0.9米,,
∴米,
∴AF=OA-OF=0.6米,DG=FQ=1.8米,
∴,
∵,
∴B′G=0.6米,
∴EG=0.3米,
∴DE=2.1米,
∴头顶距离遮阳蓬的竖直高度为2.1-1=1.1米.
故答案为:0.2,1.1
12./
解:∵点与点关于对称,
∴
又∵,
∴是等腰直角三角形,
∴,
∵点点关于对称,
∴
∵,
∴,
∴,
∴,
在中,,
∴,
∴,
∴.
故答案为:.
13.
(1) 解:过D作交于G,过C作交于K,
∵、所在直线与地面的夹角分别为,
∴,,
∵,,
∴,,
∵前后车轮半径均为,
∴扶手前端到地面的距离为: ,
故答空1为 ;
(2)解:过E作交于Q,
∵,
∴,
∵,,设为x,
∴,,
由三角函数得,
,
解得:,
∴,
故答案为 ;
14.
解:若直线EF过点J,当∠ADE=120°时,如图1所示,
由题意可知,ABCD,
∴ ∠F=∠E,∠FAJ=∠ADE=120°,
∴△FAJ∽△EDJ,
∴,
∵AF=AB+BF=50cm,DE=60cm,
∴
∴AJ=AD=cm,
过点F作FN⊥DA交DA的延长线于点N,则∠ANF=90°,
在Rt△AFN中,∠FAN=180°-∠FAJ=60°,AF=50cm,
∴FN=AFsin∠FAN=50×sin60°=25,
∴AFJ的面积=×AJ×FN=cm2;
当tan∠EDI=时,如图2所示,作EP⊥DI于点P,则∠EPD=90°,设EF交AD于点Q,
由题意可知,ABCD,
∴ ∠F=∠QED,∠FAQ=∠QDE,
∴△FAQ∽△EDQ,
∴,
∵AF=AB+BF=50cm,DE=60cm,
∴
∴DQ=AD=cm,
设EP=x,则DP=2x,由勾股定理得
,
∴,
解得x=12 cm,
∴EP=12cm,DP=24cm,PQ=DP+DQ=cm,
∴=tan∠EQP=;
当tan∠EDI=2时,如图3所示,
同理可求得DQ=cm,DP=12 cm,EP=24cm,
∴PQ=DP+DQ=cm,
∴=tan∠EQP=;
∵EF与地面的夹角α随着∠EDI的增大而增大,
∴当时,的取值范围是.
故答案为:cm2;.
15.
解:过点P作PH⊥AB于点H,如图所示:
∵,,,
∴,
∴,
∴,
∴,
∴,
若使的值为最小,也就相当于为最小,
∴当点C、P、H三点共线时,的值为最小,如图所示:
∵,
∴,
∴的最小值为;
故答案为.
16.
解:过作,为垂足,
,
,
,
,
,
,
.
故答案:.
解:如图,连接,作,为垂足,为的对应点,
,
,
,
,
设,则,
,
由题空1得:,,
,
又
,
,
即:,
整理得:,
解得:,(舍去),
.
故答案:.
17.112
解:如图,过点E作于点G,过点F作,交延长线于点M,
在中,,,
由,得,
∵,
∴,
在中,由,得,
∴.
答:挡板顶端F到地面的距离为112.
18.(1)米
(2)米
(1)解:∵小李所在斜坡的坡比为:,铅垂高度米
∴(米),
∴;
(2)解:设,如图所示,过点作于点,
∴,,则,
∵,
∴,
∴,
在中,,
∴,
解得:,
∴米.
答:无人机的高度约为21米.
19.的长和的长分别约为米和米.
解:过作于于,
∵,
∴,
∵,
∴四边形为矩形,
∵,
∴在中,,
∵米,,
∴(米),
∵,
∴在中,,
∵四边形为矩形,
∴米,
∵,
∴(米),
∴(米),
答:的长和的长分别约为米和米.
20.小宇家到劳动基地的距离约为7.1km
解:如图,过点作,垂足为.
由题意,得,
.
在中,,
∴,
.
在中,,
∴.
答:小宇家到劳动基地的距离约为7.1km.
21.(1)5.6米
(2)能,理由见解析
(1)解:斜坡的倾斜角为,
,
(米),
在中,(米),
答:在地面上距点约5.6米的处开始斜坡的施工.
(2)过作,垂足为,
,
,
,
在中,(米),
,
货车能进入地下停车场.
22.飞机飞行的高度约为米
解:过作,交的延长线于,如图所示:
设米,
由题意得:米,,,
在中,,
,
在中,,
米,
米,
,
解得:,
.
答:飞机飞行的高度约为米.
同课章节目录
