北师大版数学六年级上册1.5圆的面积(一) 教学课件(17张ppt)
文档属性
| 名称 | 北师大版数学六年级上册1.5圆的面积(一) 教学课件(17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 332.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 10:51:51 | ||
图片预览



文档简介
(共17张PPT)
第一单元 圆
圆的面积(一)
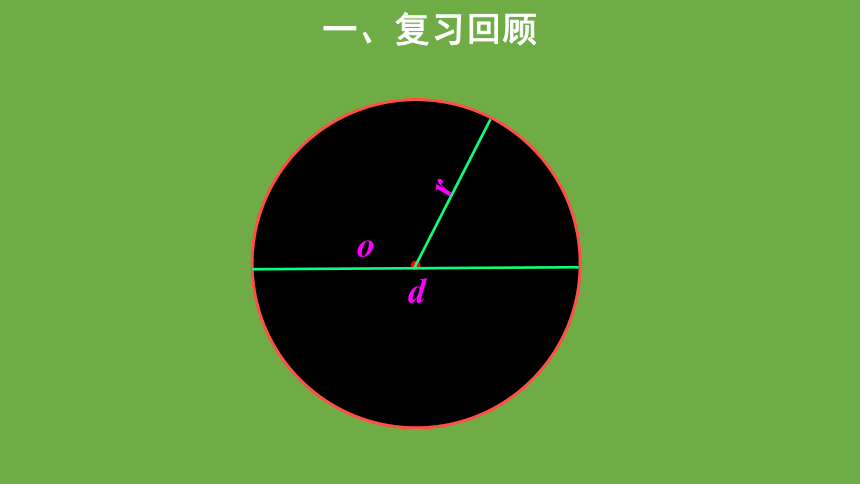
o
d
r
一、复习回顾
长方形所占平面的大小叫做长方形的面积。
一、复习回顾
圆所占平面的大小叫做圆的面积。
一、复习回顾
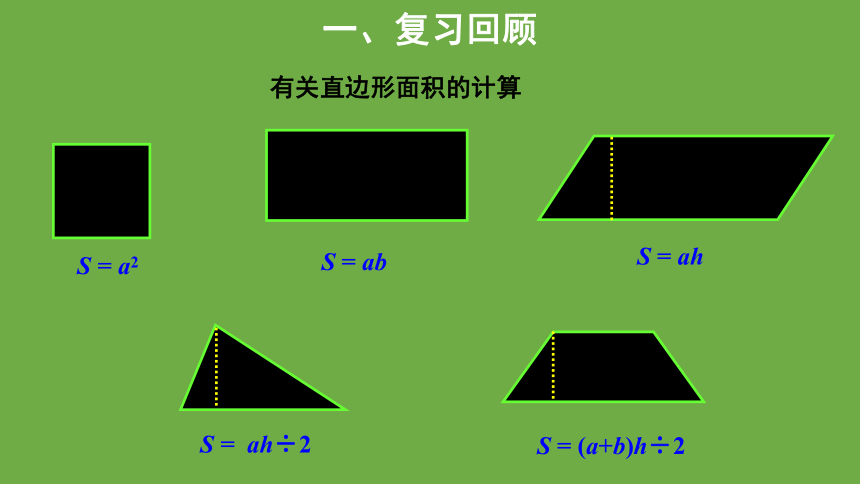
S = a2
S = ab
S = ah
S = ah÷2
S = (a+b)h÷2
有关直边形面积的计算
一、复习回顾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
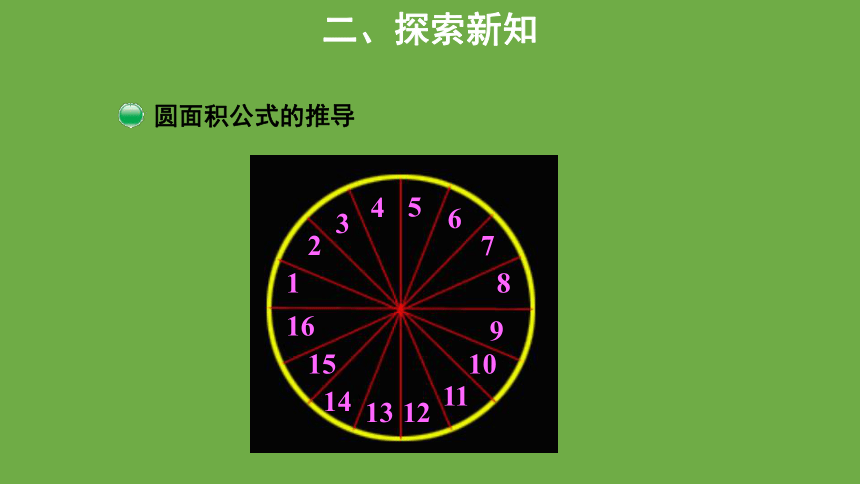
圆面积公式的推导
二、探索新知
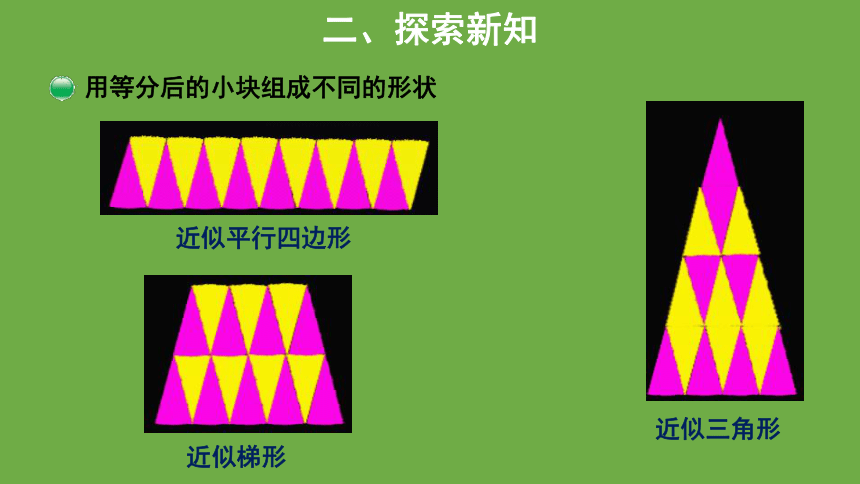
用等分后的小块组成不同的形状
近似平行四边形
近似三角形
近似梯形
二、探索新知
圆面 8 等分时:
圆面 16 等分时:
圆面 32 等分时:
以近似平行四边形为例:
等分的份数越多,拼出的图形面积越行四边形的面积。
二、探索新知
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
讨论:
1. 近似平行四边形的长与圆的周长有什么关系?
2. 近似平形四边形的宽与圆的半径有什么关系?
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
二、探索新知
结论:
1. 近似平行四边形的长与圆的周长一半大致相等。
2. 近似平形四边形的宽与圆的半径大致相等?
即:
a=πr
h=r
圆面积 近似等于 平行四边形面积
圆面积 近似等于 πr× r
二、探索新知
圆面积 等于 πr× r = πr2
由此得圆面积公式为: S = πr2
当分割无限细密时:
思考:
请同学们将分成的小块拼成右图的形状
再推导圆面积的公式。
二、探索新知
1. 你能利用方格估计下图中圆的面积吗?
圆的面积大约是
( )个小方格。
圆的面积大约是
( )个小方格。
37
148
三、巩固练习
2. 看一看,比一比,你发现了什么?
三、巩固练习
3. 如图,把一个圆分成若干等份后,还可以拼成近似的长方形。拼成
的图形与原来的圆之间有什么联系?推导一下圆的面积计算公式。
三、巩固练习
C÷2
长
宽
圆的面积
圆周长的一半
长方形的面积 = 长 × 宽
长方形的面积
圆的半径
×
×
圆的面积
2
三、巩固练习
说说你知道了什么?
四、小结
谢谢
第一单元 圆
圆的面积(一)
o
d
r
一、复习回顾
长方形所占平面的大小叫做长方形的面积。
一、复习回顾
圆所占平面的大小叫做圆的面积。
一、复习回顾
S = a2
S = ab
S = ah
S = ah÷2
S = (a+b)h÷2
有关直边形面积的计算
一、复习回顾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
圆面积公式的推导
二、探索新知
用等分后的小块组成不同的形状
近似平行四边形
近似三角形
近似梯形
二、探索新知
圆面 8 等分时:
圆面 16 等分时:
圆面 32 等分时:
以近似平行四边形为例:
等分的份数越多,拼出的图形面积越行四边形的面积。
二、探索新知
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
讨论:
1. 近似平行四边形的长与圆的周长有什么关系?
2. 近似平形四边形的宽与圆的半径有什么关系?
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
二、探索新知
结论:
1. 近似平行四边形的长与圆的周长一半大致相等。
2. 近似平形四边形的宽与圆的半径大致相等?
即:
a=πr
h=r
圆面积 近似等于 平行四边形面积
圆面积 近似等于 πr× r
二、探索新知
圆面积 等于 πr× r = πr2
由此得圆面积公式为: S = πr2
当分割无限细密时:
思考:
请同学们将分成的小块拼成右图的形状
再推导圆面积的公式。
二、探索新知
1. 你能利用方格估计下图中圆的面积吗?
圆的面积大约是
( )个小方格。
圆的面积大约是
( )个小方格。
37
148
三、巩固练习
2. 看一看,比一比,你发现了什么?
三、巩固练习
3. 如图,把一个圆分成若干等份后,还可以拼成近似的长方形。拼成
的图形与原来的圆之间有什么联系?推导一下圆的面积计算公式。
三、巩固练习
C÷2
长
宽
圆的面积
圆周长的一半
长方形的面积 = 长 × 宽
长方形的面积
圆的半径
×
×
圆的面积
2
三、巩固练习
说说你知道了什么?
四、小结
谢谢
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
