数学北师大版 六年级上册圆的面积(二)教学课件(共17张ppt)
文档属性
| 名称 | 数学北师大版 六年级上册圆的面积(二)教学课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 852.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 18:30:34 | ||
图片预览





文档简介
(共17张PPT)
第一单元 圆
圆的面积(二)
圆的面积指的是什么?
一、复习回顾
圆的面积怎样计算?说一说计算公式是怎样推导出来的?
3 m
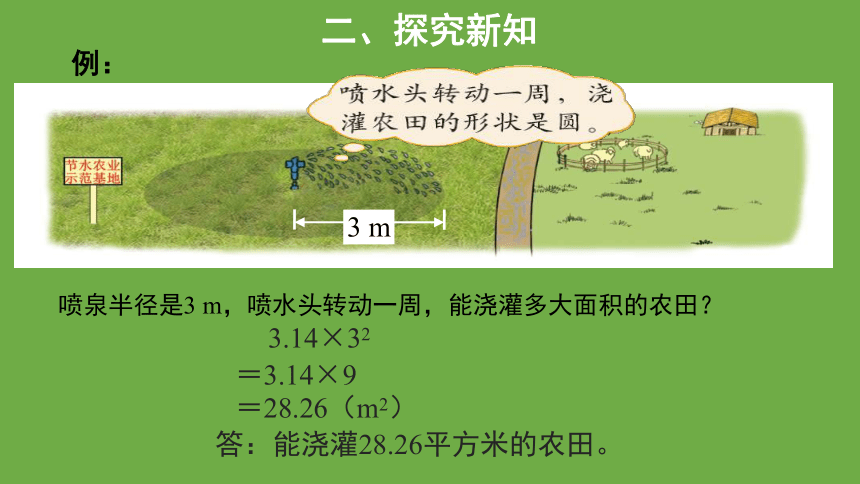
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26平方米的农田。
例:
喷泉半径是3 m,喷水头转动一周,能浇灌多大面积的农田?
二、探究新知
3 m
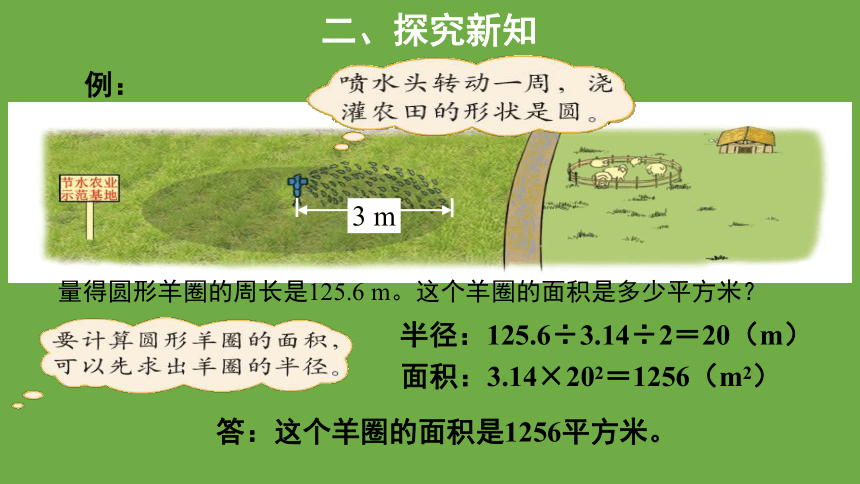
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256平方米。
面积:3.14×202=1256(m2)
例:
量得圆形羊圈的周长是125.6 m。这个羊圈的面积是多少平方米?
二、探究新知
这是一个由草绳编织成的圆形茶杯垫片。
下面是一种有意思的推导圆面积的方法,试一试,沿线剪开。
二、探究新知
r
二、探究新知
想一想,什么变了,什么没变?
沿线剪开
周长
半径
二、探究新知
想一想:在等积变形的过程中,前后图形有什么关系?如何利用这种等积变形推导出圆的面积公式的呢?
沿线剪开
?
圆形茶杯垫片如果沿直线剪开会怎样呢?
二、探究新知
想一想
圆形茶杯垫片沿直线剪开,得到两个近似的三角形,再拼成平行四边形。
二、探究新知
想一想
1.郊区有一个圆形的鱼塘,它的周长是94.2米,求鱼塘的面积是多少平方米?
94.2÷3.14÷2
=30÷2
=15(米)
(1)鱼塘的半径:
(2)鱼塘的面积 :
3.14×15
=3.14×225
=706.5(平方米)
2
答:鱼塘的面积是706.5平方米。
三、巩固练习
2.北京天坛公园的回音壁是闻名世界的声学奇迹,它是一道圆形围墙。圆的直径约为61.5米,周长与面积分别是多少?(结果保留一位小数)
周长:3.14×61.5≈193.1(m)
面积:3.14×(61.5÷2)2
≈2969.1(m2)
三、巩固练习
3.我们学校操场跑道的形状与大小如图。两边是半圆形,中间是长方形,这个运动场的占地面积是多少?
长方形面积:50×20=1000(m2)
圆面积:3.14×(20÷2)2=314(m2)
占地面积:1000+314=1314(m2)
三、巩固练习
4.一个圆环,内圆半径是8 cm,外圆半径是12 cm。它的面积是多少?
圆环面积= -
第一步求外圆面积;
第二步求内圆面积;
第三步求环形的面积。
外圆面积
内圆面积
三、巩固练习
4.一个圆环,内圆半径是8 cm,外圆半径是12 cm。它的面积是多少?
三、巩固练习
圆环面积=
外圆面积-内圆面积
3.14×122 - 3.14×82
=3.14×(122 – 82 )
=3.14×80
=251.2(cm2)
答:它的面积是251.2平方厘米。
四、课堂小结
通过本节课的学习我们知道了什么?
1.运用圆的面积公式计算圆的面积,并能运用圆面积知识解决一些简单实际的问题。
2.通过剪杯垫的演示,学会了圆面积的推导方法。体会“等积变形”的数学思想。
五、拓展延伸
求圆环的面积有很多种情况,如:
(1)已知圆环内、外圆的周长;
(2)已知内圆半径和环宽;
(3)已知外圆半径和环宽;
(4)已知内圆直径和环宽;
(5)已知外圆直径和环宽;
(6)已知内圆周长和环宽;
(7)已知外圆周长和环宽.
不管哪种情况,一般都是先求出外圆和内圆的半径,再根据:
来解答.
再见
第一单元 圆
圆的面积(二)
圆的面积指的是什么?
一、复习回顾
圆的面积怎样计算?说一说计算公式是怎样推导出来的?
3 m
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26平方米的农田。
例:
喷泉半径是3 m,喷水头转动一周,能浇灌多大面积的农田?
二、探究新知
3 m
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256平方米。
面积:3.14×202=1256(m2)
例:
量得圆形羊圈的周长是125.6 m。这个羊圈的面积是多少平方米?
二、探究新知
这是一个由草绳编织成的圆形茶杯垫片。
下面是一种有意思的推导圆面积的方法,试一试,沿线剪开。
二、探究新知
r
二、探究新知
想一想,什么变了,什么没变?
沿线剪开
周长
半径
二、探究新知
想一想:在等积变形的过程中,前后图形有什么关系?如何利用这种等积变形推导出圆的面积公式的呢?
沿线剪开
?
圆形茶杯垫片如果沿直线剪开会怎样呢?
二、探究新知
想一想
圆形茶杯垫片沿直线剪开,得到两个近似的三角形,再拼成平行四边形。
二、探究新知
想一想
1.郊区有一个圆形的鱼塘,它的周长是94.2米,求鱼塘的面积是多少平方米?
94.2÷3.14÷2
=30÷2
=15(米)
(1)鱼塘的半径:
(2)鱼塘的面积 :
3.14×15
=3.14×225
=706.5(平方米)
2
答:鱼塘的面积是706.5平方米。
三、巩固练习
2.北京天坛公园的回音壁是闻名世界的声学奇迹,它是一道圆形围墙。圆的直径约为61.5米,周长与面积分别是多少?(结果保留一位小数)
周长:3.14×61.5≈193.1(m)
面积:3.14×(61.5÷2)2
≈2969.1(m2)
三、巩固练习
3.我们学校操场跑道的形状与大小如图。两边是半圆形,中间是长方形,这个运动场的占地面积是多少?
长方形面积:50×20=1000(m2)
圆面积:3.14×(20÷2)2=314(m2)
占地面积:1000+314=1314(m2)
三、巩固练习
4.一个圆环,内圆半径是8 cm,外圆半径是12 cm。它的面积是多少?
圆环面积= -
第一步求外圆面积;
第二步求内圆面积;
第三步求环形的面积。
外圆面积
内圆面积
三、巩固练习
4.一个圆环,内圆半径是8 cm,外圆半径是12 cm。它的面积是多少?
三、巩固练习
圆环面积=
外圆面积-内圆面积
3.14×122 - 3.14×82
=3.14×(122 – 82 )
=3.14×80
=251.2(cm2)
答:它的面积是251.2平方厘米。
四、课堂小结
通过本节课的学习我们知道了什么?
1.运用圆的面积公式计算圆的面积,并能运用圆面积知识解决一些简单实际的问题。
2.通过剪杯垫的演示,学会了圆面积的推导方法。体会“等积变形”的数学思想。
五、拓展延伸
求圆环的面积有很多种情况,如:
(1)已知圆环内、外圆的周长;
(2)已知内圆半径和环宽;
(3)已知外圆半径和环宽;
(4)已知内圆直径和环宽;
(5)已知外圆直径和环宽;
(6)已知内圆周长和环宽;
(7)已知外圆周长和环宽.
不管哪种情况,一般都是先求出外圆和内圆的半径,再根据:
来解答.
再见
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
