期末常考专题:解决问题的策略(单元测试)-小学数学五年级下册苏教版(含答案)
文档属性
| 名称 | 期末常考专题:解决问题的策略(单元测试)-小学数学五年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 10:43:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末常考专题:解决问题的策略(单元测试)-小学数学五年级下册苏教版
一、选择题
1.根据37037×3=111111,37037×6=222222,37037×9=333333,那么37037×18=( )。
A.444444 B.555555 C.666666 D.999999
2.把一根10米长的细绳分别围成以下三个图形,( )的面积最小。
A.长方形 B.正方形 C.圆 D.无法判断
3.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A.20 B.24 C.28 D.32
4.根据规律算一算。
……
( )
A. B. C. D.
5.用18.84米篱包围成一块菜地,围成( )的面积最大。
A.长方形 B.正方形 C.圆 D.平行四边形
6.可以用( )简便计算。
A. B. C. D.
二、填空题
7.把原来不太规则或比较复杂的图形( )成我们已经学过的比较简单的图形,这样就容易比较,它们的形状发生变化,但面积并( )变化,“转化”是一种很巧妙的策略。
8.已知△+△+○=19,△+○=12,那么○=( )。
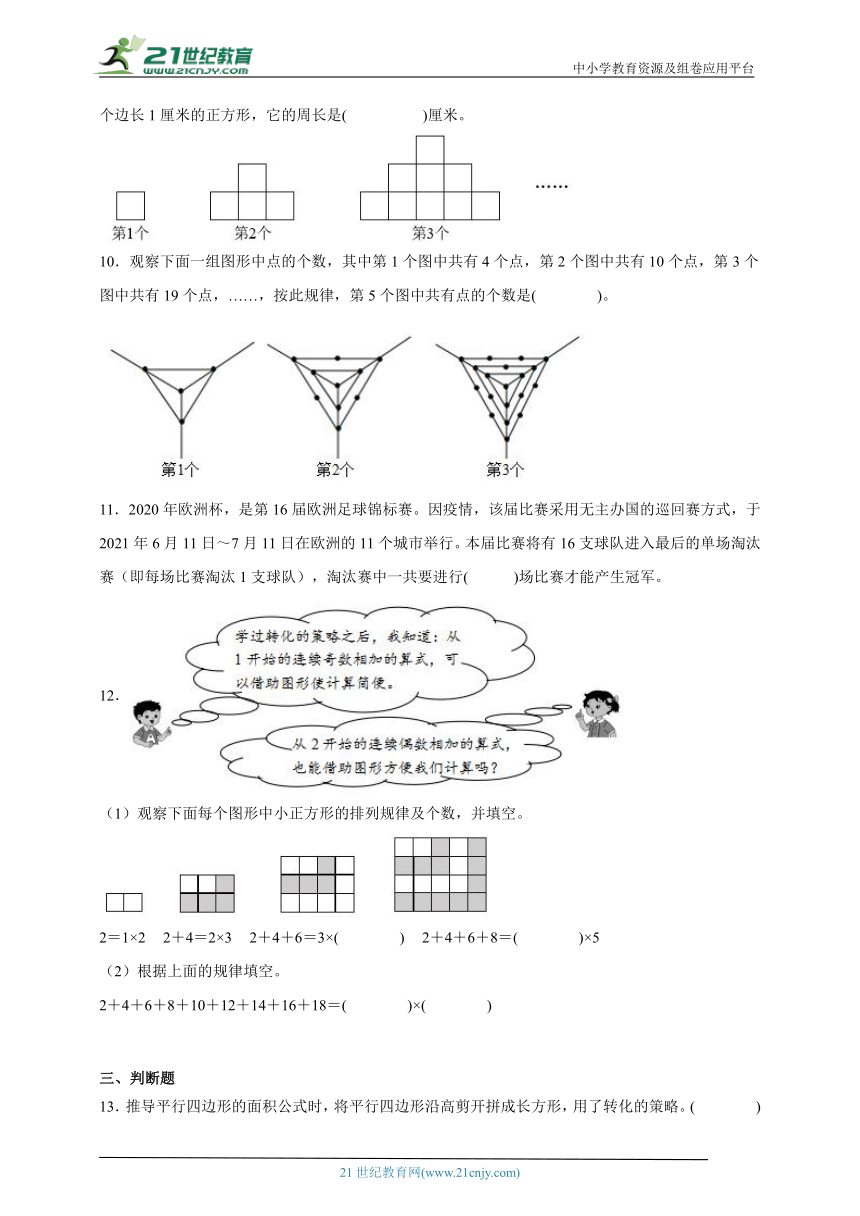
9.小华用边长1厘米的正方形纸片分别摆出下面的图形,按这样摆下去,第6个图形要用( )个边长1厘米的正方形,它的周长是( )厘米。
10.观察下面一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律,第5个图中共有点的个数是( )。
11.2020年欧洲杯,是第16届欧洲足球锦标赛。因疫情,该届比赛采用无主办国的巡回赛方式,于2021年6月11日~7月11日在欧洲的11个城市举行。本届比赛将有16支球队进入最后的单场淘汰赛(即每场比赛淘汰1支球队),淘汰赛中一共要进行( )场比赛才能产生冠军。
12.
(1)观察下面每个图形中小正方形的排列规律及个数,并填空。
2=1×2 2+4=2×3 2+4+6=3×( ) 2+4+6+8=( )×5
(2)根据上面的规律填空。
2+4+6+8+10+12+14+16+18=( )×( )
三、判断题
13.推导平行四边形的面积公式时,将平行四边形沿高剪开拼成长方形,用了转化的策略。( )
14.如图,每个小方格的面积是1cm2,草莓图的面积约是11cm2。( )
15.把平行四边形像下图那样割补成长方形,周长变小,面积不变。( )
16.根据33×4=132,333×4=1332,3333×4=13332,可知33333×4=133332。( )
17.一条毛毛虫长到成虫,每天长一倍,8天能长到40厘米,长到10厘米时是第6天。( )
四、图形计算
18.求下图中阴影部分面积。(单位:厘米)
19.计算下图图形的周长。
五、解答题
20.明明和童童在400米的跑道上同起点同向而行,明明20分钟后追上童童,已知明明的速度是每分钟100米,问童童速度每分钟多少米?
21.一块长80米、宽50米的长方形绿化带,中间有两条宽1米的小路,其余地方为草坪。草坪的面积是多少平方米?
22.解放路实验学校报告厅共有25排座位。其中第一排有10个座位,第二排有12个座位,后面每一排的座位都比前一排多2个。解放路实验学校的报告厅一共有多少个座位?
23.一个长5厘米、宽2.7厘米的长方形,沿对角线对折后,得到如图所示的几何图形,阴影部分的周长是多少厘米?
24.如果参加2008年奥运会的足球队有32支,自始至终用淘汰制进行比赛。
(1)全部比赛一共需要多少场?
(2)如果每天安排3场比赛,全部比赛大约需要多少天?
参考答案:
1.C
【分析】根据积的变化规律:一个因数不变,另一个因数扩大到原来的多少倍(0除外),积也扩大到原来的多少倍,据此解答即可。
【详解】37037×3=111111
37037×6=222222
37037×9=333333
那么37037×18=666666
故本题答案为:C。
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
2.A
【分析】已知三个图形的周长,可以根据圆的周长公式可得r=C÷π÷2,再根据圆的面积公式S=πr2,求出圆的面积;根据正方形的周长公式可得a=C÷4,求出正方形的边长,再根据正方形的面积=a2,求出正方形的面积;周长一定,也就是长方形长与宽的和一定,当长与宽越接近时面积越大,当长与宽相等时面积最大,此时是正方形,也就是正方形的面积大于长方形的面,再比较求出圆的面积和正方形的面积即可得出结论。
【详解】(1)圆的半径:10÷3.14÷2≈1.6(米);
则圆的面积为:3.14×1.62=8.0384(平方米)
(2)正方形的面积:正方形的边长为10÷4=2.5(米)
正方形面积为:2.5×2.5=6.25(平方米)
(3)而周长一定时正方形的面积比长方形的面积大
8.0384>6.25,
由以上计算可以得出,当周长一定时,圆的面积最大,长方形的面积最小。
故答案选:A
【点睛】解决本题要明确:周长相等的平面图形中,圆的面积最大;以及两个数的和一定,这两个数越接近时乘积越大。
3.B
【分析】阴影部分是由一个三角形和小正方形组成的。正方形的面积=边长×边长,据此可以求出小正方形的面积。用阴影部分的面积减去小正方形的面积即是三角形的面积,三角形的高是4厘米,根据三角形的面积=底×高÷2,可以求出三角形的底,即是大正方形的边长。求出大正方形的面积,再减去三角形的面积就是空白部分的面积。
【详解】28-4×4=12(平方厘米)
12×2÷4=6(厘米)
6×6-12=24(平方厘米)
故答案为:B
【点睛】用阴影部分的面积减去小正方形的面积求出三角形的面积,继而求出三角形的底是解题的关键。
4.D
【解析】从所给算式可以看出:算式等号左边都是连续的偶数,右边的结果为:偶数的个数×(个数+1),即n×(n+1),据此解答。
【详解】由分析可得,10×(10+1)=10×11;
故答案为:D
【点睛】观察特例特点,找出规律,根据规律进行解答。
5.C
【分析】周长相等的平面图形中,圆的面积最大,据此解题即可。
【详解】围成圆的面积最大。
故答案为:C。
【点睛】本题考查了平面图形的面积,明确周长一致的情况下圆的面积最大是解题的关键。
6.B
【分析】算式是计算从1到25一共13个单数的和。
可以先从简单数据着手找规律:1=1×1
1+3=4=2×2
1+3+5=9=3×3
1+3+5+7=16=4×4
……
可以发现,连续n个奇数的和=n2=n×n;据此解答即可。
【详解】从1到25一共13个单数,由分析可得,=13×13;
故答案为:B
【点睛】解答此类问题要认真观察,根据数字特点进行分析,从而达到巧算的目的。
7. 转化 没有
【详解】把原来不太规则或比较复杂的图形转化成我们已经学过的比较简单的图形,这样就容易比较,它们的形状发生变化,但面积并没有变化,“转化”是一种很巧妙的策略。如运用拼补法把圆的面积转化为长方形的面积进行计算,从而推导出圆的面积公式。
8.5
【分析】根据题意,将△+○=12代入△+△+○=19中,求出△的值,进而求出○的值。
【详解】12+△=19
12-12△=19-12
△=7
7+○=12
7-7○=12-7
○=5
【点睛】本题考查了等量代换的知识点,一定要找到两个算式的关系。
9. 36 34
【分析】仔细观察给出的图形,并结合图中的层数、正方形的个数和周长,可以发现:正方形的个数=层数×层数;周长=6×层数-2;据此解答即可。
【详解】6×6=36(个)
6×6-2
=36-2
=34(厘米)
第6个图形要用36个边长1厘米的正方形,它的周长是34厘米。
【点睛】本题主要考查数与形结合的规律,关键是根据图示发现这组图形的规律,利用规律做题。
10.46
【分析】由图可知:第一个图形中共有1+1×3=4(个)点,第二个图形中共有1+1×3+2×3=10(个)点,第三个图形中共有1+1×3+2×3+3×3=19(个)点,……由此得出第n个图形有1+1×3+2×3+3×3+……+3n个点。
【详解】由分析可知,第5个图中共有点的个数是:
1+1×3+2×3+3×3+4×3+5×3
=1+3+6+9+12+15
=19+27
=46(个)
【点睛】本题考查数形结合问题。找出图形之间的数字运算规律,利用规律解题是关键。
11.15
【分析】由题意可知,每淘汰1支球队就要进行1场比赛。推理即得出:淘汰赛比赛场数=参加队伍数-1,然后把参加队伍数16代入计算即可。
【详解】因为:16-1=15(场)
所以:淘汰赛中一共要进行15场比赛后才能产生冠军。
【点睛】本题考查灵活使用转化策略解决实际问题的能力,掌握在单场淘汰制中比赛的场数与参赛队数的关系是解题关键。
12. 4 4 9 10
【分析】(1)第一个图由2个小正方形组成,它的面积可以写成2=1×2;第二个图由6个小正方形组成,它的面积可以写成2+4=2×3;第三个图由10个小正方形组成,它的面积是2+4+6=3×4;第四个图由20个小正方形组成,它的面积是2+4+6+8=4×5。由此得出规律:得数是偶数的个数(即序号)与偶数个数加1的积,据此解答。
(2)根据第(1)题得出的规律,2+4+6+8+10+12+14+16+18中偶数的个数有9个,所以2+4+6+8+10+12+14+16+18=9×10=90。据此作答。
【详解】根据分析可知:
(1)2+4+6=3×4=12,2+4+6+8=4×5=20
(2)2+4+6+8+10+12+14+16+18=9×10=90
【点睛】本题考查了转化策略的运用,将连续偶数相加求和转化为图形面积问题方便计算。
13.√
【分析】平行四边形、三角形、梯形的面积公式的推导都是通过转化的方法进行推导的,据此解答。
【详解】我们在学习平行四边形面积公式推导时,是将平行四边形沿高剪开,拼成一个长方形来学习的,这一过程中运用了转化的数学思想方法。
故答案为:√
【点睛】此题考查的目的是理解掌握平行四边形面积公式的推导过程及应用。
14.√
【分析】如图,看成两个三角形,根据三角形面积=底×高÷2,分别求出两个三角形面积,再相加,接近11平方厘米即可。
【详解】4×2÷2+4×3÷2
=4+6
=10(平方厘米)
草莓图的面积约是11cm2,说法正确。
故答案为:√
【点睛】借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
15.√
【分析】把一个平行四边形通过割补转化成一个长方形,这时,平行四边形的底相当于长方形的长,高相当于长方形的宽,由于斜边大于直角边,所以平行四边形的周长变小了;根据长方形的面积=长×宽和平行四边形的面积=底×高,可知面积未发生变化。
【详解】把平行四边形像图形那样割补成长方形,由于外斜边变短了,周长也变小了;但是平行四边形的底相当于长方形的长,高相当于长方形的宽,根据面积公式可知,面积未变。
故答案为:√
【点睛】此题主要考查了学生利用知识的迁移推导平行四边形面积公式时,平行四边形的周长和面积的变化。
16.√
【分析】根据观察知:第2个因数都是4,其结果最高位都是1、最低位都是2、中间都是3,3的个数比第一个因数中3的个数少1,据此解答。
【详解】33×4=132
333×4=1332
3333×4=13332
可知:33333×4=133332
故答案为:√
【点睛】找出算式中各个因数的变化规律是解题的关键。
17.√
【分析】根据题意知道,一条毛毛虫由幼虫长成成虫,每天长大一倍,8天能长到40厘米,逆推知道7天就长到20厘米,6天就长到10厘米,由此得出答案。
【详解】第8天能长到40厘米,
第7天能长到:40÷2=20(厘米)
第6天能长到:20÷2=10(厘米)
所以原题说法正确.
故答案为:√
【点睛】解答此题的关键是,根据题意,运用逆推的方法,不难得出答案。
18.25平方厘米
【分析】利用平移和转化的思想,将右边正方形中的阴影平移到图形最左边,则阴影部分正好是一个边长为5厘米的正方形。
【详解】如图:;将图①平移到图②位置,则阴影部分面积等于边长是5厘米的正方形面积。
5×5=25(平方厘米)
19.100厘米
【分析】本题主要利用长方形的周长计算公式为:(长+宽)×2,代入数值进行计算。
【详解】通过转化将图形的周长转化成长方形的周长:
(32+18)×2
=50×2
=100(厘米)
【点睛】利用转化法求图形的周长是本题的关键。
20.80米
【分析】明明20分钟后追上童童,此时明明比童童走一圈(400米);根据速度×时间=路程,代入数据求出明明20分钟所走的路程,明明的路程减去400米求出童童20分钟所走的路程,再根据速度=路程÷时间,代入数据求出童童的速度即可。
【详解】(100×20-400)÷20
=(2000-400)÷20
=1600÷20
=80(米)
答:童童速度每分钟80米。
【点睛】本题主要考查追及问题,理解“明明20分钟后追上童童”是解题的关键。
21.3871平方米
【分析】观察图形可知,草坪的面积等于长(80-1)米、宽(50-1)米的长方形的面积,根据“长方形面积=长×宽”,即可解题。
【详解】(80-1)×(50-1)
=79×49
=3871(平方米)
答:草坪的面积是3871平方米。
【点睛】熟记长方形面积计算公式,是解答此题的关键。
22.850个
【分析】根据已知条件,第一排有10个座位,后面每排都比前面一排多2个座位,则:第二排有:10+1×2=12(个);第三排有:10+2×2=14(个);第四排有:10+3×2=16(个)……第n排有:10+(n-1)×2;所以第25排有:10+(25-1)×2=58(个),据此求出第25排有多少个座位;
因为后面每一排的座位都比前一排多2个,所以座位排列为梯形,梯形的上底长为第一排座位数,下底长为最后一排座位数,高为排数;利用梯形面积公式“梯形面积=(上底+下底)×高÷2”解答。
【详解】10+(25-1)×2
=10+24×2
=10+48
=58(个)
(10+58)×25÷2
=68×25÷2
=1700÷2
=850(个)
答:解放路实验学校的报告厅一共有850个座位。
【点睛】灵活利用梯形的面积公式是解答题目的关键。
23.15.4厘米
【分析】因为下边是沿对角线对折后得到的图形,所以BF=AB,DF=AD,所以,DF+BF+BC+CD=(5+2.7)×2,据此解答。
【详解】(5+2.7)×2
=7.7×2
=15.4(厘米)
答:阴影部分的周长是15.4厘米。
【点睛】此题考查了学生对图形的分析能力,可以亲自动手折一折,很容易得出结果。
24.(1)31场
(2)11天
【分析】(1)每一轮的比赛场数是球队数的一半,每进行一轮淘汰赛球队就剩下原来的一半,直到只剩一只球队;
(2)比赛总场数÷每天安排比赛场数即可求出天数。
【详解】(1)第一轮:32÷2=16(场)
第二轮:16÷2=8(场)
第三轮:8÷2=4(场)
第四轮:4÷2=2(场)
第五轮:2÷2=1(场)
16+8+4+2+1=31(场)
答:全部比赛一共需要31场。
(2)31÷3≈11(天)
答:全部比赛大约需要11天。
【点睛】问题(2),因为要把全部的比赛进行完,所以计算结果要用进一法保留整数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末常考专题:解决问题的策略(单元测试)-小学数学五年级下册苏教版
一、选择题
1.根据37037×3=111111,37037×6=222222,37037×9=333333,那么37037×18=( )。
A.444444 B.555555 C.666666 D.999999
2.把一根10米长的细绳分别围成以下三个图形,( )的面积最小。
A.长方形 B.正方形 C.圆 D.无法判断
3.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A.20 B.24 C.28 D.32
4.根据规律算一算。
……
( )
A. B. C. D.
5.用18.84米篱包围成一块菜地,围成( )的面积最大。
A.长方形 B.正方形 C.圆 D.平行四边形
6.可以用( )简便计算。
A. B. C. D.
二、填空题
7.把原来不太规则或比较复杂的图形( )成我们已经学过的比较简单的图形,这样就容易比较,它们的形状发生变化,但面积并( )变化,“转化”是一种很巧妙的策略。
8.已知△+△+○=19,△+○=12,那么○=( )。
9.小华用边长1厘米的正方形纸片分别摆出下面的图形,按这样摆下去,第6个图形要用( )个边长1厘米的正方形,它的周长是( )厘米。
10.观察下面一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律,第5个图中共有点的个数是( )。
11.2020年欧洲杯,是第16届欧洲足球锦标赛。因疫情,该届比赛采用无主办国的巡回赛方式,于2021年6月11日~7月11日在欧洲的11个城市举行。本届比赛将有16支球队进入最后的单场淘汰赛(即每场比赛淘汰1支球队),淘汰赛中一共要进行( )场比赛才能产生冠军。
12.
(1)观察下面每个图形中小正方形的排列规律及个数,并填空。
2=1×2 2+4=2×3 2+4+6=3×( ) 2+4+6+8=( )×5
(2)根据上面的规律填空。
2+4+6+8+10+12+14+16+18=( )×( )
三、判断题
13.推导平行四边形的面积公式时,将平行四边形沿高剪开拼成长方形,用了转化的策略。( )
14.如图,每个小方格的面积是1cm2,草莓图的面积约是11cm2。( )
15.把平行四边形像下图那样割补成长方形,周长变小,面积不变。( )
16.根据33×4=132,333×4=1332,3333×4=13332,可知33333×4=133332。( )
17.一条毛毛虫长到成虫,每天长一倍,8天能长到40厘米,长到10厘米时是第6天。( )
四、图形计算
18.求下图中阴影部分面积。(单位:厘米)
19.计算下图图形的周长。
五、解答题
20.明明和童童在400米的跑道上同起点同向而行,明明20分钟后追上童童,已知明明的速度是每分钟100米,问童童速度每分钟多少米?
21.一块长80米、宽50米的长方形绿化带,中间有两条宽1米的小路,其余地方为草坪。草坪的面积是多少平方米?
22.解放路实验学校报告厅共有25排座位。其中第一排有10个座位,第二排有12个座位,后面每一排的座位都比前一排多2个。解放路实验学校的报告厅一共有多少个座位?
23.一个长5厘米、宽2.7厘米的长方形,沿对角线对折后,得到如图所示的几何图形,阴影部分的周长是多少厘米?
24.如果参加2008年奥运会的足球队有32支,自始至终用淘汰制进行比赛。
(1)全部比赛一共需要多少场?
(2)如果每天安排3场比赛,全部比赛大约需要多少天?
参考答案:
1.C
【分析】根据积的变化规律:一个因数不变,另一个因数扩大到原来的多少倍(0除外),积也扩大到原来的多少倍,据此解答即可。
【详解】37037×3=111111
37037×6=222222
37037×9=333333
那么37037×18=666666
故本题答案为:C。
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
2.A
【分析】已知三个图形的周长,可以根据圆的周长公式可得r=C÷π÷2,再根据圆的面积公式S=πr2,求出圆的面积;根据正方形的周长公式可得a=C÷4,求出正方形的边长,再根据正方形的面积=a2,求出正方形的面积;周长一定,也就是长方形长与宽的和一定,当长与宽越接近时面积越大,当长与宽相等时面积最大,此时是正方形,也就是正方形的面积大于长方形的面,再比较求出圆的面积和正方形的面积即可得出结论。
【详解】(1)圆的半径:10÷3.14÷2≈1.6(米);
则圆的面积为:3.14×1.62=8.0384(平方米)
(2)正方形的面积:正方形的边长为10÷4=2.5(米)
正方形面积为:2.5×2.5=6.25(平方米)
(3)而周长一定时正方形的面积比长方形的面积大
8.0384>6.25,
由以上计算可以得出,当周长一定时,圆的面积最大,长方形的面积最小。
故答案选:A
【点睛】解决本题要明确:周长相等的平面图形中,圆的面积最大;以及两个数的和一定,这两个数越接近时乘积越大。
3.B
【分析】阴影部分是由一个三角形和小正方形组成的。正方形的面积=边长×边长,据此可以求出小正方形的面积。用阴影部分的面积减去小正方形的面积即是三角形的面积,三角形的高是4厘米,根据三角形的面积=底×高÷2,可以求出三角形的底,即是大正方形的边长。求出大正方形的面积,再减去三角形的面积就是空白部分的面积。
【详解】28-4×4=12(平方厘米)
12×2÷4=6(厘米)
6×6-12=24(平方厘米)
故答案为:B
【点睛】用阴影部分的面积减去小正方形的面积求出三角形的面积,继而求出三角形的底是解题的关键。
4.D
【解析】从所给算式可以看出:算式等号左边都是连续的偶数,右边的结果为:偶数的个数×(个数+1),即n×(n+1),据此解答。
【详解】由分析可得,10×(10+1)=10×11;
故答案为:D
【点睛】观察特例特点,找出规律,根据规律进行解答。
5.C
【分析】周长相等的平面图形中,圆的面积最大,据此解题即可。
【详解】围成圆的面积最大。
故答案为:C。
【点睛】本题考查了平面图形的面积,明确周长一致的情况下圆的面积最大是解题的关键。
6.B
【分析】算式是计算从1到25一共13个单数的和。
可以先从简单数据着手找规律:1=1×1
1+3=4=2×2
1+3+5=9=3×3
1+3+5+7=16=4×4
……
可以发现,连续n个奇数的和=n2=n×n;据此解答即可。
【详解】从1到25一共13个单数,由分析可得,=13×13;
故答案为:B
【点睛】解答此类问题要认真观察,根据数字特点进行分析,从而达到巧算的目的。
7. 转化 没有
【详解】把原来不太规则或比较复杂的图形转化成我们已经学过的比较简单的图形,这样就容易比较,它们的形状发生变化,但面积并没有变化,“转化”是一种很巧妙的策略。如运用拼补法把圆的面积转化为长方形的面积进行计算,从而推导出圆的面积公式。
8.5
【分析】根据题意,将△+○=12代入△+△+○=19中,求出△的值,进而求出○的值。
【详解】12+△=19
12-12△=19-12
△=7
7+○=12
7-7○=12-7
○=5
【点睛】本题考查了等量代换的知识点,一定要找到两个算式的关系。
9. 36 34
【分析】仔细观察给出的图形,并结合图中的层数、正方形的个数和周长,可以发现:正方形的个数=层数×层数;周长=6×层数-2;据此解答即可。
【详解】6×6=36(个)
6×6-2
=36-2
=34(厘米)
第6个图形要用36个边长1厘米的正方形,它的周长是34厘米。
【点睛】本题主要考查数与形结合的规律,关键是根据图示发现这组图形的规律,利用规律做题。
10.46
【分析】由图可知:第一个图形中共有1+1×3=4(个)点,第二个图形中共有1+1×3+2×3=10(个)点,第三个图形中共有1+1×3+2×3+3×3=19(个)点,……由此得出第n个图形有1+1×3+2×3+3×3+……+3n个点。
【详解】由分析可知,第5个图中共有点的个数是:
1+1×3+2×3+3×3+4×3+5×3
=1+3+6+9+12+15
=19+27
=46(个)
【点睛】本题考查数形结合问题。找出图形之间的数字运算规律,利用规律解题是关键。
11.15
【分析】由题意可知,每淘汰1支球队就要进行1场比赛。推理即得出:淘汰赛比赛场数=参加队伍数-1,然后把参加队伍数16代入计算即可。
【详解】因为:16-1=15(场)
所以:淘汰赛中一共要进行15场比赛后才能产生冠军。
【点睛】本题考查灵活使用转化策略解决实际问题的能力,掌握在单场淘汰制中比赛的场数与参赛队数的关系是解题关键。
12. 4 4 9 10
【分析】(1)第一个图由2个小正方形组成,它的面积可以写成2=1×2;第二个图由6个小正方形组成,它的面积可以写成2+4=2×3;第三个图由10个小正方形组成,它的面积是2+4+6=3×4;第四个图由20个小正方形组成,它的面积是2+4+6+8=4×5。由此得出规律:得数是偶数的个数(即序号)与偶数个数加1的积,据此解答。
(2)根据第(1)题得出的规律,2+4+6+8+10+12+14+16+18中偶数的个数有9个,所以2+4+6+8+10+12+14+16+18=9×10=90。据此作答。
【详解】根据分析可知:
(1)2+4+6=3×4=12,2+4+6+8=4×5=20
(2)2+4+6+8+10+12+14+16+18=9×10=90
【点睛】本题考查了转化策略的运用,将连续偶数相加求和转化为图形面积问题方便计算。
13.√
【分析】平行四边形、三角形、梯形的面积公式的推导都是通过转化的方法进行推导的,据此解答。
【详解】我们在学习平行四边形面积公式推导时,是将平行四边形沿高剪开,拼成一个长方形来学习的,这一过程中运用了转化的数学思想方法。
故答案为:√
【点睛】此题考查的目的是理解掌握平行四边形面积公式的推导过程及应用。
14.√
【分析】如图,看成两个三角形,根据三角形面积=底×高÷2,分别求出两个三角形面积,再相加,接近11平方厘米即可。
【详解】4×2÷2+4×3÷2
=4+6
=10(平方厘米)
草莓图的面积约是11cm2,说法正确。
故答案为:√
【点睛】借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
15.√
【分析】把一个平行四边形通过割补转化成一个长方形,这时,平行四边形的底相当于长方形的长,高相当于长方形的宽,由于斜边大于直角边,所以平行四边形的周长变小了;根据长方形的面积=长×宽和平行四边形的面积=底×高,可知面积未发生变化。
【详解】把平行四边形像图形那样割补成长方形,由于外斜边变短了,周长也变小了;但是平行四边形的底相当于长方形的长,高相当于长方形的宽,根据面积公式可知,面积未变。
故答案为:√
【点睛】此题主要考查了学生利用知识的迁移推导平行四边形面积公式时,平行四边形的周长和面积的变化。
16.√
【分析】根据观察知:第2个因数都是4,其结果最高位都是1、最低位都是2、中间都是3,3的个数比第一个因数中3的个数少1,据此解答。
【详解】33×4=132
333×4=1332
3333×4=13332
可知:33333×4=133332
故答案为:√
【点睛】找出算式中各个因数的变化规律是解题的关键。
17.√
【分析】根据题意知道,一条毛毛虫由幼虫长成成虫,每天长大一倍,8天能长到40厘米,逆推知道7天就长到20厘米,6天就长到10厘米,由此得出答案。
【详解】第8天能长到40厘米,
第7天能长到:40÷2=20(厘米)
第6天能长到:20÷2=10(厘米)
所以原题说法正确.
故答案为:√
【点睛】解答此题的关键是,根据题意,运用逆推的方法,不难得出答案。
18.25平方厘米
【分析】利用平移和转化的思想,将右边正方形中的阴影平移到图形最左边,则阴影部分正好是一个边长为5厘米的正方形。
【详解】如图:;将图①平移到图②位置,则阴影部分面积等于边长是5厘米的正方形面积。
5×5=25(平方厘米)
19.100厘米
【分析】本题主要利用长方形的周长计算公式为:(长+宽)×2,代入数值进行计算。
【详解】通过转化将图形的周长转化成长方形的周长:
(32+18)×2
=50×2
=100(厘米)
【点睛】利用转化法求图形的周长是本题的关键。
20.80米
【分析】明明20分钟后追上童童,此时明明比童童走一圈(400米);根据速度×时间=路程,代入数据求出明明20分钟所走的路程,明明的路程减去400米求出童童20分钟所走的路程,再根据速度=路程÷时间,代入数据求出童童的速度即可。
【详解】(100×20-400)÷20
=(2000-400)÷20
=1600÷20
=80(米)
答:童童速度每分钟80米。
【点睛】本题主要考查追及问题,理解“明明20分钟后追上童童”是解题的关键。
21.3871平方米
【分析】观察图形可知,草坪的面积等于长(80-1)米、宽(50-1)米的长方形的面积,根据“长方形面积=长×宽”,即可解题。
【详解】(80-1)×(50-1)
=79×49
=3871(平方米)
答:草坪的面积是3871平方米。
【点睛】熟记长方形面积计算公式,是解答此题的关键。
22.850个
【分析】根据已知条件,第一排有10个座位,后面每排都比前面一排多2个座位,则:第二排有:10+1×2=12(个);第三排有:10+2×2=14(个);第四排有:10+3×2=16(个)……第n排有:10+(n-1)×2;所以第25排有:10+(25-1)×2=58(个),据此求出第25排有多少个座位;
因为后面每一排的座位都比前一排多2个,所以座位排列为梯形,梯形的上底长为第一排座位数,下底长为最后一排座位数,高为排数;利用梯形面积公式“梯形面积=(上底+下底)×高÷2”解答。
【详解】10+(25-1)×2
=10+24×2
=10+48
=58(个)
(10+58)×25÷2
=68×25÷2
=1700÷2
=850(个)
答:解放路实验学校的报告厅一共有850个座位。
【点睛】灵活利用梯形的面积公式是解答题目的关键。
23.15.4厘米
【分析】因为下边是沿对角线对折后得到的图形,所以BF=AB,DF=AD,所以,DF+BF+BC+CD=(5+2.7)×2,据此解答。
【详解】(5+2.7)×2
=7.7×2
=15.4(厘米)
答:阴影部分的周长是15.4厘米。
【点睛】此题考查了学生对图形的分析能力,可以亲自动手折一折,很容易得出结果。
24.(1)31场
(2)11天
【分析】(1)每一轮的比赛场数是球队数的一半,每进行一轮淘汰赛球队就剩下原来的一半,直到只剩一只球队;
(2)比赛总场数÷每天安排比赛场数即可求出天数。
【详解】(1)第一轮:32÷2=16(场)
第二轮:16÷2=8(场)
第三轮:8÷2=4(场)
第四轮:4÷2=2(场)
第五轮:2÷2=1(场)
16+8+4+2+1=31(场)
答:全部比赛一共需要31场。
(2)31÷3≈11(天)
答:全部比赛大约需要11天。
【点睛】问题(2),因为要把全部的比赛进行完,所以计算结果要用进一法保留整数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
