高考考前“状态保持”强化训练-2023届高三数学三轮冲刺(含解析)
文档属性
| 名称 | 高考考前“状态保持”强化训练-2023届高三数学三轮冲刺(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 00:00:00 | ||
图片预览




文档简介
高考考前“状态保持”强化训练
考前常态化!
(2)简单题怎样做才不会粗心错!(简单题不丢分,难题尽量得分!!)
(3)排除法、代入法、特殊值(图形)法、数形结合法、二级结论秒杀,找规律,甚至可以量长度......
(4)计算、计算、计算!特别是草稿纸上的运算!
(5)最后一个月找考试的状态!
(6)碰到难题(没思路、算不对、太费时....),做好标记暂时跳过!
(7)大小题的压轴训练,一定要保持!但不宜做难度太大的题了!------让思维保持最佳状态!!!!!
一、多项选择题
1、已知函数,的定义域均为R,且满足,
,,则( )
A. B.
C.的图象关于点对称 D.
2、已知函数,则下列结论正确的是( )
A.当时,若有三个零点,则b的取值范围为
B.若满足,则
C.若过点可作出曲线的三条切线,则
D.若存在极值点,且,其中,则
3、在平面直角坐标系Oxy中,为等腰三角形,顶角,点为AB的中点,记的面积,则( )
A. B.S的最大值为6
C.的最大值为6 D.点B的轨迹方程是
二、选择题
4、已知双曲线的离心率为3,斜率为的直线分别交F的左,右两支于A,B两点,直线分别交F的左,右两支于C,D两点,,AC交BD于点E,点E恒在直线l上,若直线l的斜率存在,则直线l的方程为( )
A. B. C. D.
5、已知,,曲线上存在点,使得,则a的范围是( )
A. B. C. D.
6、如图,在梯形ABCD中,,,,将沿AC边折起,使得点D翻折到点P,若三棱锥的外接球表面积为,则( )
A.8 B.4 C. D.2
三、填空题
7、已知函数在处取得极大值,则实数a的取值范围是________.
8、已知点在抛物线上,过点A作圆的两条切线分别交抛物线于B,C两点,则直线BC的方程为____________.
9、已知双曲线,,分别为双曲线的左 右焦点,P为双曲线上的第一象限内的点,点I为△的内心,点I在x轴上的投影H的横坐标为___________, 的面积的取值范围为___________.
四、解答题
10、一企业生产某种产品,通过加大技术创新投入降低了每件产品成本,为了调查年技术创新投入x (单位:千万元)对每件产品成本y (单位:元)的影响,对近10年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得:,,,,.
(1)根据散点图可知,可用函数模型拟合y与x的关系,
试建立y关于x的回归方程;
(2)已知该产品的年销售额m (单位:千万元)与每件产品成本y的关系
为.该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据(1)的结果回答:当年技术创新投入x为何值时,年利润的预报值最大?
(注:年利润=年销售额一年投入成本)
参考公式:对于一组数据、、……、,其回归直线的斜率和截距的最小乘估计分别为:,.
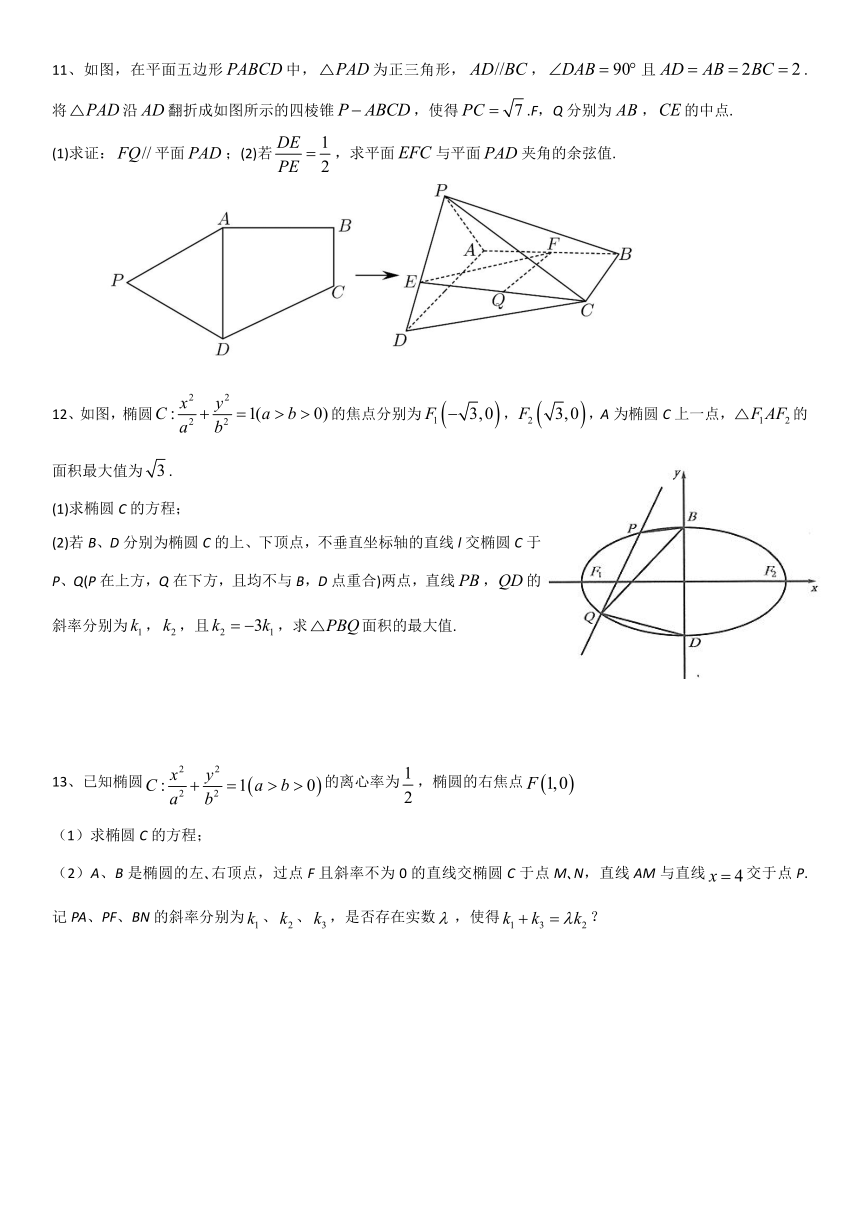
11、如图,在平面五边形中,为正三角形,,且.将沿翻折成如图所示的四棱锥,使得.F,Q分别为,的中点.
(1)求证:平面;(2)若,求平面与平面夹角的余弦值.
12、如图,椭圆的焦点分别为,,A为椭圆C上一点,的面积最大值为.
(1)求椭圆C的方程;
(2)若B、D分别为椭圆C的上、下顶点,不垂直坐标轴的直线l交椭圆C于P、Q(P在上方,Q在下方,且均不与B,D点重合)两点,直线,的斜率分别为,,且,求面积的最大值.
13、已知椭圆的离心率为,椭圆的右焦点
(1)求椭圆C的方程;
(2)A、B是椭圆的左 右顶点,过点F且斜率不为0的直线交椭圆C于点M N,直线AM与直线交于点P.记PA、PF、BN的斜率分别为、、,是否存在实数,使得?
14、已知函数,.
(1)求函数的极值点;
(2)若恒成立,求实数m的取值范围.
15、已知函数,.
(1)当时,,求实数a的取值范围;
(2)已知,证明:.
16、已知函数.
(1)求函数的单调区间;
(2)若函数有两个零点,,证明:
答案解析
一、多项选择题
1、已知函数,的定义域均为R,且满足,,,则( )
A. B.
C.的图象关于点对称 D.
【答案】
1、答案:AD
解析:因为,所以的图象关于点对称,所以,因为,所以,即,因为,所以,代入得,即,A正确;因为定义域为R的函数的图象关于点对称,所以,B错误;由,得,即,.因为,所以,又因为,相减得,所以的图象关于点中心对称,C错误;因为函数的定义域为R,所以,所以.记,,则数列是以3为首项,为公差的等差数列,数列是以2为首项,为公差的等差数列,故,,所以,D正确,故选AD.
2、已知函数,则下列结论正确的是( )
A.当时,若有三个零点,则b的取值范围为
B.若满足,则
C.若过点可作出曲线的三条切线,则
D.若存在极值点,且,其中,则
【答案】
2、答案: 答案:ACD
解析:对于A ,,当时,,,
令,解得或,
在上单调递增,在上单调递减,在上单调递增;
当时取得极大值,当时取得极小值,
有三个零点,,解得,故选项A正确;
对于B ,满足,根据函数的对称可知的对称点为,将其代入,得,
解得,故选项B错误;
对于C ,,
设切点为,则切线的斜率
化简,
得
由条件可知该方程有三个实根,有三个实根,
记,
令,解得或,
当时取得极大值,当时,取得极小值,
因为过点可作出曲线的三条切线,
所以,解得,故选项C正确;
对于D ,,,
当,在上单调递增;
当,在上单调递增,在上单调递减,在上单调递增;
存在极值点,
由得
令,
,于是,
所以
,
化简得:,
,,于是,
.故选项D正确;
故选:ACD.
3、在平面直角坐标系Oxy中,为等腰三角形,顶角,点为AB的中点,记的面积,则( )
A.
B.S的最大值为6
C.的最大值为6
D.点B的轨迹方程是
【答案】
3、答案: ABD
解析:由,,为AB的中点,
若且,则,
故,
整理得:,则A轨迹是圆心为,半径为2的圆(去掉与x轴交点),
如下图,由圆的对称性,不妨令A在轨迹圆的上半部分,即,
令,则,
所以,则,
所以,A正确;
由,
则S的最大值为6,B正确;
由下图知:,所以无最大值,C错误;
令,则.代入A轨迹得,
即,
所以B轨迹为且,D正确;
故选:ABD.
二、选择题
4、已知双曲线的离心率为3,斜率为的直线分别交F的左,右两支于A,B两点,直线分别交F的左,右两支于C,D两点,,AC交BD于点E,点E恒在直线l上,若直线l的斜率存在,则直线l的方程为( )
A. B. C. D.
【答案】
4、答案:A
解析:由题得,设,,,,,AB的中点,CD的中点,则,相减得,所以.,所以①,同理得②,因为,则E,M,N三点共线,所以,将①②代入得,即,所以,即点E在直线上,故选A.
5、已知,,曲线上存在点,使得,则a的范围是( )
A. B. C. D.
【答案】
5、答案: B
解析:因为,所以,
由题意上存在一点使得,
即,只需证明,显然为增函数,
假设,则不满足,
同理不满足,
所以,那么函数即函数在有解,
即,可得,
从而,令,
则,
令,即,解得(舍去),
时, 时,
所以在单调递增,所以,
,,
所以的取值范围为,
即a的取值范围为.
故选:B.
6、如图,在梯形ABCD中,,,,将沿AC边折起,使得点D翻折到点P,若三棱锥的外接球表面积为,则( )
A.8 B.4 C. D.2
【答案】
6、答案:C
解析:如图,设M为AC的中点,为AB的中点,
为的外心,O为三棱锥的外接球球心,
则面ABC,面APC.
由题意得, 为的外心,
设外接球半径为R,
则,即,而, ,
在中,易得,即,由得,四边形为平行四边形,而面ABC,即,四边形为矩形,即面APC,面APC,
,,
故选C.
三、填空题
7、已知函数在处取得极大值,则实数a的取值范围是________.
【答案】
7、答案:
解析:,可得,令,则.①当时,,在R上单调递增,当时,,所以,在上单调递减;当时,,所以,在上单调递增,所以在处取得极小值,不合题意;②当时,,令,解得,在上单调递增,可得当时,,从而,在上单调递减;当时,,从而,在上单调递增,所以在处取得极小值,不合题意;③当时,,令,解得,令,解得,所以在上单调递增,在上单调递减,所以在处取得极大值,也是最大值,所以,从而,所以在R上单调递减,不合题意;④当时,,同理可知在上单调递减,故当时,,从而,在上单调递增,当时,,从而,在上单调递减.所以在处取得极大值,符合题意.综上,实数a的取值范围为.
8、已知点在抛物线上,过点A作圆的两条切线分别交抛物线于B,C两点,则直线BC的方程为____________.
【答案】
8、答案:
解析:因为点在抛物线上,则,解得,即抛物线方程为,
显然过点A作圆的两条切线斜率存在,设此切线方程为,即,
于是,解得,设点,
不妨令直线的斜率分别为,于是,,
同理,直线的斜率,而点,
直线BC的方程为,即.
故答案为:
9、已知双曲线,,分别为双曲线的左 右焦点,P为双曲线上的第一象限内的点,点I为△的内心,点I在x轴上的投影H的横坐标为___________, 的面积的取值范围为___________.
【答案】
9、答案:①3②
解析:由题意得:,故,
设点,且I在上垂足为H,
根据双曲线定义及切线长定理得:,
又,解得:,
所以点H坐标为,即横坐标为3;
渐近线的倾斜角为,则,
记,则,
所以,即,
又,解得:(负值舍),
所以,则,
所以.
故答案为:3,
四、解答题
10、一企业生产某种产品,通过加大技术创新投入降低了每件产品成本,为了调查年技术创新投入x (单位:千万元)对每件产品成本y (单位:元)的影响,对近10年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得:,,,,.
(1)根据散点图可知,可用函数模型拟合y与x的关系,试建立y关于x的回归方程;
(2)已知该产品的年销售额m (单位:千万元)与每件产品成本y的关系为.该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据(1)的结果回答:当年技术创新投入x为何值时,年利润的预报值最大?
(注:年利润=年销售额一年投入成本)
参考公式:对于一组数据、、……、,其回归直线的斜率和截距的最小乘估计分别为:,.
【答案】
10、答案:(1)
(2)当年技术创新投入为千万元时,年利润的预报值取最大值
解析:(1)令,则y关于u的线性回归方程为,
由题意可得,
,则,
所以,y关于x的回归方程为.
(2)解:由可得,
年利润
,
当时,年利润M取得最大值,此时,
所以,当年技术创新投入为20千万元时,年利润的预报值取最大值.
11、如图,在平面五边形中,为正三角形,,且.将沿翻折成如图所示的四棱锥,使得.F,Q分别为,的中点.
(1)求证:平面;
(2)若,求平面与平面夹角的余弦值.
【答案】
11、答案:(1)证明见解析
(2)
解析:(1)证明:取的中点M,连接,.
则,.
因为面,面,
所以,面,面,
因为,
所以,面面,
因为面,所以面.
(2)取的中点O,连接,,
因为为正三角形,,所以且,
在直角梯形中,,,,
所以,且,
又因为,
所以在中,,即,
所以,以O为坐标原点,分别以,,的方向为x,y,z轴的正向,建立如图所示的空间直角坐标系,
则,,,,.
因为,即,,
所以,,
所以,.
设为平面的一个法向量,
则,即,取.
又平面的一个法向量,
设平面与平面夹角为,
.
12、如图,椭圆的焦点分别为,,A为椭圆C上一点,的面积最大值为.
(1)求椭圆C的方程;
(2)若B、D分别为椭圆C的上、下顶点,不垂直坐标轴的直线l交椭圆C于P、Q(P在上方,Q在下方,且均不与B,D点重合)两点,直线,的斜率分别为,,且,求面积的最大值.
【答案】
12、答案:(1)
(2)面积的最大值为
解析:(1),,,
故椭圆C的方程为;
(2)依题意设直线的方程为,,,
联立方程组,消元得:,
,,
,
由得:,
两边同乘,,
即;
将,代入上式得:
,
整理得:,所以或(舍),
,
当时等号成立,满足条件,所以面积的最大值为.
13、已知椭圆的离心率为,椭圆的右焦点
(1)求椭圆C的方程;
(2)A、B是椭圆的左 右顶点,过点F且斜率不为0的直线交椭圆C于点M N,直线AM与直线交于点P.记PA、PF、BN的斜率分别为、、,是否存在实数,使得?
【答案】
13、答案:(1)
(2)见解析
解析:(1)因为椭圆的离心率为,椭圆的右焦点,
所以,,,则,故,
因此,椭圆C的方程为.
(2)证明:设、,设直线MN的方程为,其中,
联立,得,,
由韦达定理可得,,
所以,
易知点、,,
所以,直线AM的方程为,
将代入直线AM的方程可得,即点,
,,
所以,,
所以,.
14、已知函数,.
(1)求函数的极值点;
(2)若恒成立,求实数m的取值范围.
【答案】
(1)答案:是的极大值点,无极小值点
解析:由已知可得,函数的定义域为,且,
当时,;当时,,
所以的单调递增区间为,单调递减区间为,
所以是的极大值点,无极小值点.
(2)答案:当时,恒成立
解析:设,,
则,
令,,
则对任意恒成立,
所以在上单调递减.
又,,
所以,使得,即,则,
即.
因此,当时,,即,则单调递增;
当时,,即,则单调递减,
故,解得,
所以当时,恒成立.
14、已知函数,.
(1)当时,,求实数a的取值范围;
(2)已知,证明:.
【答案】
14、答案:(1)
(2)证明见解析
解析:(1)解:令,则,
当时,,则函数在上单调递增,
当时,,则函数在上单调递减,
所以,,即,
所以,当时,,即,
当时,取,
由于,而,得,
故,不合乎题意.
综上所述,.
(2)证明:当时,由(1)可得,则,
可得,即,即,
令,所以,,所以,,即,
所以,,,
令,则,且不恒为零,
所以,函数上单调递增,故,则,
所以,,,
所以,
.
15、已知函数.
(1)求函数的单调区间;
(2)若函数有两个零点,,证明:
【答案】
15、答案:(1)见解析
(2)见解析
解析:(1),令,解得,
令,解得,
所以的单调减区间为
单调增区间为
(2)证明不妨设,由(1)知.
要证,即证,即证,
又,即证.
令,,
则
令,则在上恒成立,
所以在上单调递减,即在上单调递减,
所以
所以在上单调递增,所以,所以
令,,又,即,所以
要证,即证,有,两边取对数,
即证,即证
即证
令,,,
可得函数单调递增,可得,即,
所以
综上,
证明的另一种方法:
不妨设,由(1)可知,必有
可得
若,由函数的单调性可得,
又由,有
.
令,有可得函数单调递减,
有
又由,可得,
故有不等式成立.
考前常态化!
(2)简单题怎样做才不会粗心错!(简单题不丢分,难题尽量得分!!)
(3)排除法、代入法、特殊值(图形)法、数形结合法、二级结论秒杀,找规律,甚至可以量长度......
(4)计算、计算、计算!特别是草稿纸上的运算!
(5)最后一个月找考试的状态!
(6)碰到难题(没思路、算不对、太费时....),做好标记暂时跳过!
(7)大小题的压轴训练,一定要保持!但不宜做难度太大的题了!------让思维保持最佳状态!!!!!
一、多项选择题
1、已知函数,的定义域均为R,且满足,
,,则( )
A. B.
C.的图象关于点对称 D.
2、已知函数,则下列结论正确的是( )
A.当时,若有三个零点,则b的取值范围为
B.若满足,则
C.若过点可作出曲线的三条切线,则
D.若存在极值点,且,其中,则
3、在平面直角坐标系Oxy中,为等腰三角形,顶角,点为AB的中点,记的面积,则( )
A. B.S的最大值为6
C.的最大值为6 D.点B的轨迹方程是
二、选择题
4、已知双曲线的离心率为3,斜率为的直线分别交F的左,右两支于A,B两点,直线分别交F的左,右两支于C,D两点,,AC交BD于点E,点E恒在直线l上,若直线l的斜率存在,则直线l的方程为( )
A. B. C. D.
5、已知,,曲线上存在点,使得,则a的范围是( )
A. B. C. D.
6、如图,在梯形ABCD中,,,,将沿AC边折起,使得点D翻折到点P,若三棱锥的外接球表面积为,则( )
A.8 B.4 C. D.2
三、填空题
7、已知函数在处取得极大值,则实数a的取值范围是________.
8、已知点在抛物线上,过点A作圆的两条切线分别交抛物线于B,C两点,则直线BC的方程为____________.
9、已知双曲线,,分别为双曲线的左 右焦点,P为双曲线上的第一象限内的点,点I为△的内心,点I在x轴上的投影H的横坐标为___________, 的面积的取值范围为___________.
四、解答题
10、一企业生产某种产品,通过加大技术创新投入降低了每件产品成本,为了调查年技术创新投入x (单位:千万元)对每件产品成本y (单位:元)的影响,对近10年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得:,,,,.
(1)根据散点图可知,可用函数模型拟合y与x的关系,
试建立y关于x的回归方程;
(2)已知该产品的年销售额m (单位:千万元)与每件产品成本y的关系
为.该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据(1)的结果回答:当年技术创新投入x为何值时,年利润的预报值最大?
(注:年利润=年销售额一年投入成本)
参考公式:对于一组数据、、……、,其回归直线的斜率和截距的最小乘估计分别为:,.
11、如图,在平面五边形中,为正三角形,,且.将沿翻折成如图所示的四棱锥,使得.F,Q分别为,的中点.
(1)求证:平面;(2)若,求平面与平面夹角的余弦值.
12、如图,椭圆的焦点分别为,,A为椭圆C上一点,的面积最大值为.
(1)求椭圆C的方程;
(2)若B、D分别为椭圆C的上、下顶点,不垂直坐标轴的直线l交椭圆C于P、Q(P在上方,Q在下方,且均不与B,D点重合)两点,直线,的斜率分别为,,且,求面积的最大值.
13、已知椭圆的离心率为,椭圆的右焦点
(1)求椭圆C的方程;
(2)A、B是椭圆的左 右顶点,过点F且斜率不为0的直线交椭圆C于点M N,直线AM与直线交于点P.记PA、PF、BN的斜率分别为、、,是否存在实数,使得?
14、已知函数,.
(1)求函数的极值点;
(2)若恒成立,求实数m的取值范围.
15、已知函数,.
(1)当时,,求实数a的取值范围;
(2)已知,证明:.
16、已知函数.
(1)求函数的单调区间;
(2)若函数有两个零点,,证明:
答案解析
一、多项选择题
1、已知函数,的定义域均为R,且满足,,,则( )
A. B.
C.的图象关于点对称 D.
【答案】
1、答案:AD
解析:因为,所以的图象关于点对称,所以,因为,所以,即,因为,所以,代入得,即,A正确;因为定义域为R的函数的图象关于点对称,所以,B错误;由,得,即,.因为,所以,又因为,相减得,所以的图象关于点中心对称,C错误;因为函数的定义域为R,所以,所以.记,,则数列是以3为首项,为公差的等差数列,数列是以2为首项,为公差的等差数列,故,,所以,D正确,故选AD.
2、已知函数,则下列结论正确的是( )
A.当时,若有三个零点,则b的取值范围为
B.若满足,则
C.若过点可作出曲线的三条切线,则
D.若存在极值点,且,其中,则
【答案】
2、答案: 答案:ACD
解析:对于A ,,当时,,,
令,解得或,
在上单调递增,在上单调递减,在上单调递增;
当时取得极大值,当时取得极小值,
有三个零点,,解得,故选项A正确;
对于B ,满足,根据函数的对称可知的对称点为,将其代入,得,
解得,故选项B错误;
对于C ,,
设切点为,则切线的斜率
化简,
得
由条件可知该方程有三个实根,有三个实根,
记,
令,解得或,
当时取得极大值,当时,取得极小值,
因为过点可作出曲线的三条切线,
所以,解得,故选项C正确;
对于D ,,,
当,在上单调递增;
当,在上单调递增,在上单调递减,在上单调递增;
存在极值点,
由得
令,
,于是,
所以
,
化简得:,
,,于是,
.故选项D正确;
故选:ACD.
3、在平面直角坐标系Oxy中,为等腰三角形,顶角,点为AB的中点,记的面积,则( )
A.
B.S的最大值为6
C.的最大值为6
D.点B的轨迹方程是
【答案】
3、答案: ABD
解析:由,,为AB的中点,
若且,则,
故,
整理得:,则A轨迹是圆心为,半径为2的圆(去掉与x轴交点),
如下图,由圆的对称性,不妨令A在轨迹圆的上半部分,即,
令,则,
所以,则,
所以,A正确;
由,
则S的最大值为6,B正确;
由下图知:,所以无最大值,C错误;
令,则.代入A轨迹得,
即,
所以B轨迹为且,D正确;
故选:ABD.
二、选择题
4、已知双曲线的离心率为3,斜率为的直线分别交F的左,右两支于A,B两点,直线分别交F的左,右两支于C,D两点,,AC交BD于点E,点E恒在直线l上,若直线l的斜率存在,则直线l的方程为( )
A. B. C. D.
【答案】
4、答案:A
解析:由题得,设,,,,,AB的中点,CD的中点,则,相减得,所以.,所以①,同理得②,因为,则E,M,N三点共线,所以,将①②代入得,即,所以,即点E在直线上,故选A.
5、已知,,曲线上存在点,使得,则a的范围是( )
A. B. C. D.
【答案】
5、答案: B
解析:因为,所以,
由题意上存在一点使得,
即,只需证明,显然为增函数,
假设,则不满足,
同理不满足,
所以,那么函数即函数在有解,
即,可得,
从而,令,
则,
令,即,解得(舍去),
时, 时,
所以在单调递增,所以,
,,
所以的取值范围为,
即a的取值范围为.
故选:B.
6、如图,在梯形ABCD中,,,,将沿AC边折起,使得点D翻折到点P,若三棱锥的外接球表面积为,则( )
A.8 B.4 C. D.2
【答案】
6、答案:C
解析:如图,设M为AC的中点,为AB的中点,
为的外心,O为三棱锥的外接球球心,
则面ABC,面APC.
由题意得, 为的外心,
设外接球半径为R,
则,即,而, ,
在中,易得,即,由得,四边形为平行四边形,而面ABC,即,四边形为矩形,即面APC,面APC,
,,
故选C.
三、填空题
7、已知函数在处取得极大值,则实数a的取值范围是________.
【答案】
7、答案:
解析:,可得,令,则.①当时,,在R上单调递增,当时,,所以,在上单调递减;当时,,所以,在上单调递增,所以在处取得极小值,不合题意;②当时,,令,解得,在上单调递增,可得当时,,从而,在上单调递减;当时,,从而,在上单调递增,所以在处取得极小值,不合题意;③当时,,令,解得,令,解得,所以在上单调递增,在上单调递减,所以在处取得极大值,也是最大值,所以,从而,所以在R上单调递减,不合题意;④当时,,同理可知在上单调递减,故当时,,从而,在上单调递增,当时,,从而,在上单调递减.所以在处取得极大值,符合题意.综上,实数a的取值范围为.
8、已知点在抛物线上,过点A作圆的两条切线分别交抛物线于B,C两点,则直线BC的方程为____________.
【答案】
8、答案:
解析:因为点在抛物线上,则,解得,即抛物线方程为,
显然过点A作圆的两条切线斜率存在,设此切线方程为,即,
于是,解得,设点,
不妨令直线的斜率分别为,于是,,
同理,直线的斜率,而点,
直线BC的方程为,即.
故答案为:
9、已知双曲线,,分别为双曲线的左 右焦点,P为双曲线上的第一象限内的点,点I为△的内心,点I在x轴上的投影H的横坐标为___________, 的面积的取值范围为___________.
【答案】
9、答案:①3②
解析:由题意得:,故,
设点,且I在上垂足为H,
根据双曲线定义及切线长定理得:,
又,解得:,
所以点H坐标为,即横坐标为3;
渐近线的倾斜角为,则,
记,则,
所以,即,
又,解得:(负值舍),
所以,则,
所以.
故答案为:3,
四、解答题
10、一企业生产某种产品,通过加大技术创新投入降低了每件产品成本,为了调查年技术创新投入x (单位:千万元)对每件产品成本y (单位:元)的影响,对近10年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得:,,,,.
(1)根据散点图可知,可用函数模型拟合y与x的关系,试建立y关于x的回归方程;
(2)已知该产品的年销售额m (单位:千万元)与每件产品成本y的关系为.该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据(1)的结果回答:当年技术创新投入x为何值时,年利润的预报值最大?
(注:年利润=年销售额一年投入成本)
参考公式:对于一组数据、、……、,其回归直线的斜率和截距的最小乘估计分别为:,.
【答案】
10、答案:(1)
(2)当年技术创新投入为千万元时,年利润的预报值取最大值
解析:(1)令,则y关于u的线性回归方程为,
由题意可得,
,则,
所以,y关于x的回归方程为.
(2)解:由可得,
年利润
,
当时,年利润M取得最大值,此时,
所以,当年技术创新投入为20千万元时,年利润的预报值取最大值.
11、如图,在平面五边形中,为正三角形,,且.将沿翻折成如图所示的四棱锥,使得.F,Q分别为,的中点.
(1)求证:平面;
(2)若,求平面与平面夹角的余弦值.
【答案】
11、答案:(1)证明见解析
(2)
解析:(1)证明:取的中点M,连接,.
则,.
因为面,面,
所以,面,面,
因为,
所以,面面,
因为面,所以面.
(2)取的中点O,连接,,
因为为正三角形,,所以且,
在直角梯形中,,,,
所以,且,
又因为,
所以在中,,即,
所以,以O为坐标原点,分别以,,的方向为x,y,z轴的正向,建立如图所示的空间直角坐标系,
则,,,,.
因为,即,,
所以,,
所以,.
设为平面的一个法向量,
则,即,取.
又平面的一个法向量,
设平面与平面夹角为,
.
12、如图,椭圆的焦点分别为,,A为椭圆C上一点,的面积最大值为.
(1)求椭圆C的方程;
(2)若B、D分别为椭圆C的上、下顶点,不垂直坐标轴的直线l交椭圆C于P、Q(P在上方,Q在下方,且均不与B,D点重合)两点,直线,的斜率分别为,,且,求面积的最大值.
【答案】
12、答案:(1)
(2)面积的最大值为
解析:(1),,,
故椭圆C的方程为;
(2)依题意设直线的方程为,,,
联立方程组,消元得:,
,,
,
由得:,
两边同乘,,
即;
将,代入上式得:
,
整理得:,所以或(舍),
,
当时等号成立,满足条件,所以面积的最大值为.
13、已知椭圆的离心率为,椭圆的右焦点
(1)求椭圆C的方程;
(2)A、B是椭圆的左 右顶点,过点F且斜率不为0的直线交椭圆C于点M N,直线AM与直线交于点P.记PA、PF、BN的斜率分别为、、,是否存在实数,使得?
【答案】
13、答案:(1)
(2)见解析
解析:(1)因为椭圆的离心率为,椭圆的右焦点,
所以,,,则,故,
因此,椭圆C的方程为.
(2)证明:设、,设直线MN的方程为,其中,
联立,得,,
由韦达定理可得,,
所以,
易知点、,,
所以,直线AM的方程为,
将代入直线AM的方程可得,即点,
,,
所以,,
所以,.
14、已知函数,.
(1)求函数的极值点;
(2)若恒成立,求实数m的取值范围.
【答案】
(1)答案:是的极大值点,无极小值点
解析:由已知可得,函数的定义域为,且,
当时,;当时,,
所以的单调递增区间为,单调递减区间为,
所以是的极大值点,无极小值点.
(2)答案:当时,恒成立
解析:设,,
则,
令,,
则对任意恒成立,
所以在上单调递减.
又,,
所以,使得,即,则,
即.
因此,当时,,即,则单调递增;
当时,,即,则单调递减,
故,解得,
所以当时,恒成立.
14、已知函数,.
(1)当时,,求实数a的取值范围;
(2)已知,证明:.
【答案】
14、答案:(1)
(2)证明见解析
解析:(1)解:令,则,
当时,,则函数在上单调递增,
当时,,则函数在上单调递减,
所以,,即,
所以,当时,,即,
当时,取,
由于,而,得,
故,不合乎题意.
综上所述,.
(2)证明:当时,由(1)可得,则,
可得,即,即,
令,所以,,所以,,即,
所以,,,
令,则,且不恒为零,
所以,函数上单调递增,故,则,
所以,,,
所以,
.
15、已知函数.
(1)求函数的单调区间;
(2)若函数有两个零点,,证明:
【答案】
15、答案:(1)见解析
(2)见解析
解析:(1),令,解得,
令,解得,
所以的单调减区间为
单调增区间为
(2)证明不妨设,由(1)知.
要证,即证,即证,
又,即证.
令,,
则
令,则在上恒成立,
所以在上单调递减,即在上单调递减,
所以
所以在上单调递增,所以,所以
令,,又,即,所以
要证,即证,有,两边取对数,
即证,即证
即证
令,,,
可得函数单调递增,可得,即,
所以
综上,
证明的另一种方法:
不妨设,由(1)可知,必有
可得
若,由函数的单调性可得,
又由,有
.
令,有可得函数单调递减,
有
又由,可得,
故有不等式成立.
同课章节目录
