关于导数与函数中“指对同构”的一点思考讲义-2023届高三数学三轮冲刺(无答案)
文档属性
| 名称 | 关于导数与函数中“指对同构”的一点思考讲义-2023届高三数学三轮冲刺(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 514.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 09:18:30 | ||
图片预览


文档简介
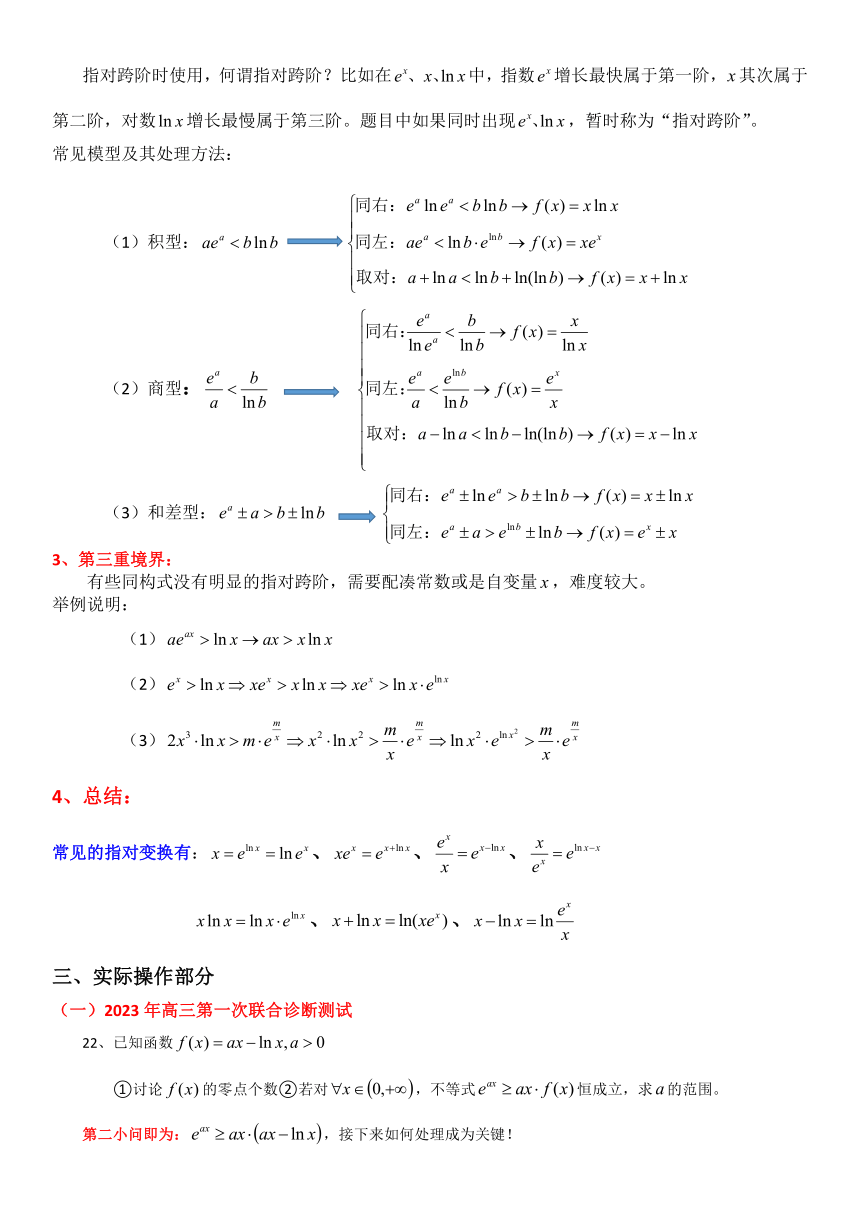
关于导数与函数中“指对同构”的一点思考
一、导数同构中的六大基础函数
另外,以下几个函数也要让学生熟悉:
、、、、、
同构的三重境界
第一重境界:
双变量问题,、地位完全相同,也称为轮换式,只需把同一变量移到不等式的同一边即可。举几个常见的例子,一目了了。
可以设
构造新函数,求导证明为增函数即可
可以设 造新函数,求导证明为增函数即可
处理方法同上。
第二重境界:
指对跨阶时使用,何谓指对跨阶?比如在中,指数增长最快属于第一阶,其次属于第二阶,对数增长最慢属于第三阶。题目中如果同时出现,暂时称为“指对跨阶”。
常见模型及其处理方法:
(1)积型:
(2)商型:
(3)和差型:
3、第三重境界:
有些同构式没有明显的指对跨阶,需要配凑常数或是自变量,难度较大。
举例说明:
4、总结:
常见的指对变换有:、、、
、、
三、实际操作部分
(一)2023年高三第一次联合诊断测试
22、已知函数
①讨论的零点个数②若对,不等式恒成立,求的范围。
第二小问即为:,接下来如何处理成为关键!
步骤:
................观察特点,适当配凑!
现在可以简化不等式,整体换元:设 求出的范围:
原不等式化为:,即:在时恒成立,求新函数在的最小值。
至此已经很简单了!!
(二)2023年南开高三第六次质量检测(2月份月考)
22、现定义:为函数在区间上的立方变化率。已知,
(2)若对任意区间,的立方变化率均大于的立方变化率,求实数的取值范围。
在上单调递增
在上恒成立
讨论:①当时显然成立(略)
②当时,先把复杂项转化:
上述不等式化为:在上恒成立
关键步骤“同构”转化
..................................观察两边的特点,适当配凑!
.........还是比较容易想到!
注意:
.................完成“同构”,下面构造函数!
设 ,显然在递增
所以有:
下面的处理就简单了,构造新函数求最值,解出参数a的范围即可!
(三)
安徽省晥优联盟2022-2023年高三联考试题压轴
已知函数
若,讨论的单调性(略)
若,求实数的取值范围。
方法1、(朗博同构+切线放缩)
由已知得:,即:
令 ,即:
,设,则
在单减,在单增,
故:,解得:,
方法2、(同构+换元)
由已知得:,即:
化简得:
令 ,则不等式化为:,即:
设,则
在单减,在单增,
故:,解得:,
方法3、(求导+隐零点)
由已知得:,设
则
令,即:,设,则
在单增,
存在唯一零点,使得:,得:
在单减,在单增,
故:,解得:,
四、函数同构思想的应用
1、设实数,若对任意的,不等式恒成立,则的取值范围是
2、设实数,若对任意的,不等式恒成立,则的取值范围是
对任意,不等式恒成立,则实数的最小值是
4、已知实数满足,则=
5、(2022年八省联考第8题)
设,若,则下面结论正确的是( )
6、(2023届高三潍坊市一模21题第2小问)
已知函数,, 证明:当时,
7、(2020年山东高考22题第2问)
已知函数,若恒成立,求实数的范围?
8、(2021年云贵川桂四省联考22题第2问)
(改编)已知函数,若方程在有两个不同的解,求实数的取值范围?
9、(长沙市一中2023届高三月考(六)22题第2问)
已知函数,若的最小值为,求实数的最大值。
一、导数同构中的六大基础函数
另外,以下几个函数也要让学生熟悉:
、、、、、
同构的三重境界
第一重境界:
双变量问题,、地位完全相同,也称为轮换式,只需把同一变量移到不等式的同一边即可。举几个常见的例子,一目了了。
可以设
构造新函数,求导证明为增函数即可
可以设 造新函数,求导证明为增函数即可
处理方法同上。
第二重境界:
指对跨阶时使用,何谓指对跨阶?比如在中,指数增长最快属于第一阶,其次属于第二阶,对数增长最慢属于第三阶。题目中如果同时出现,暂时称为“指对跨阶”。
常见模型及其处理方法:
(1)积型:
(2)商型:
(3)和差型:
3、第三重境界:
有些同构式没有明显的指对跨阶,需要配凑常数或是自变量,难度较大。
举例说明:
4、总结:
常见的指对变换有:、、、
、、
三、实际操作部分
(一)2023年高三第一次联合诊断测试
22、已知函数
①讨论的零点个数②若对,不等式恒成立,求的范围。
第二小问即为:,接下来如何处理成为关键!
步骤:
................观察特点,适当配凑!
现在可以简化不等式,整体换元:设 求出的范围:
原不等式化为:,即:在时恒成立,求新函数在的最小值。
至此已经很简单了!!
(二)2023年南开高三第六次质量检测(2月份月考)
22、现定义:为函数在区间上的立方变化率。已知,
(2)若对任意区间,的立方变化率均大于的立方变化率,求实数的取值范围。
在上单调递增
在上恒成立
讨论:①当时显然成立(略)
②当时,先把复杂项转化:
上述不等式化为:在上恒成立
关键步骤“同构”转化
..................................观察两边的特点,适当配凑!
.........还是比较容易想到!
注意:
.................完成“同构”,下面构造函数!
设 ,显然在递增
所以有:
下面的处理就简单了,构造新函数求最值,解出参数a的范围即可!
(三)
安徽省晥优联盟2022-2023年高三联考试题压轴
已知函数
若,讨论的单调性(略)
若,求实数的取值范围。
方法1、(朗博同构+切线放缩)
由已知得:,即:
令 ,即:
,设,则
在单减,在单增,
故:,解得:,
方法2、(同构+换元)
由已知得:,即:
化简得:
令 ,则不等式化为:,即:
设,则
在单减,在单增,
故:,解得:,
方法3、(求导+隐零点)
由已知得:,设
则
令,即:,设,则
在单增,
存在唯一零点,使得:,得:
在单减,在单增,
故:,解得:,
四、函数同构思想的应用
1、设实数,若对任意的,不等式恒成立,则的取值范围是
2、设实数,若对任意的,不等式恒成立,则的取值范围是
对任意,不等式恒成立,则实数的最小值是
4、已知实数满足,则=
5、(2022年八省联考第8题)
设,若,则下面结论正确的是( )
6、(2023届高三潍坊市一模21题第2小问)
已知函数,, 证明:当时,
7、(2020年山东高考22题第2问)
已知函数,若恒成立,求实数的范围?
8、(2021年云贵川桂四省联考22题第2问)
(改编)已知函数,若方程在有两个不同的解,求实数的取值范围?
9、(长沙市一中2023届高三月考(六)22题第2问)
已知函数,若的最小值为,求实数的最大值。
同课章节目录
