苏教版数学六年级下册 第二单元 圆柱和圆锥-第三课时 圆柱的体积课件(共29张PPT)
文档属性
| 名称 | 苏教版数学六年级下册 第二单元 圆柱和圆锥-第三课时 圆柱的体积课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 09:56:12 | ||
图片预览








文档简介
(共29张PPT)
六年级数学下册教学课件(苏教版)
第二单元 圆柱和圆锥
第三课时 圆柱的体积
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
我们在推导圆的面积公式时,是把它转化成近似的长方形,找到这个长方形与圆各部分之间的联系,由长方形的面积公式推导出了圆的面积公式。
探索与发现
02
探索与发现
探索与发现
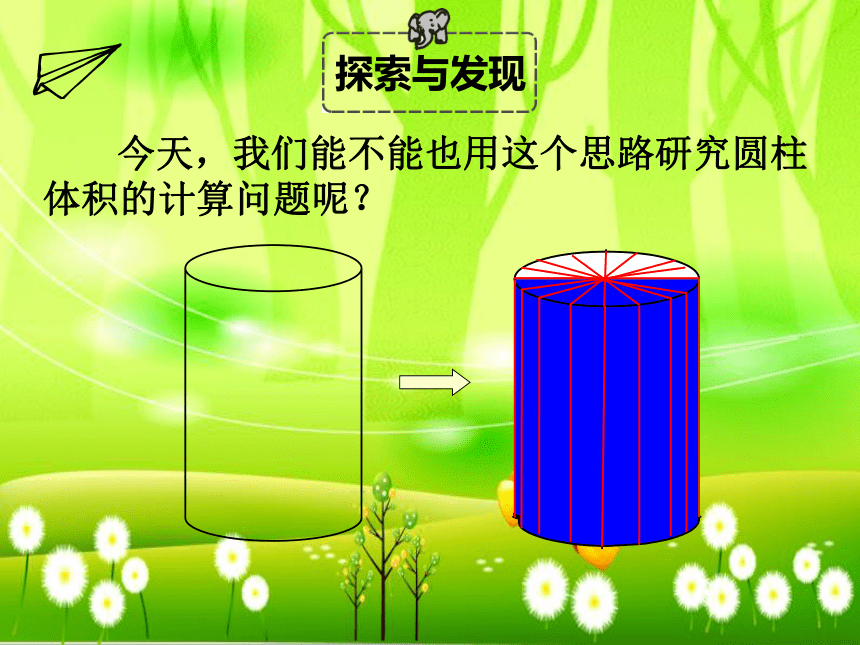
今天,我们能不能也用这个思路研究圆柱体积的计算问题呢?
探索与发现
下面的长方体、正方体和圆柱的底面积相等,高也相等。
(1)长方体与正方体的体积相等吗?为什么?
(2)猜一猜,圆柱的体积与长方体、正方体的体积相等吗?用什么办法验证呢?
探索与发现
探索与发现
圆可以转化成近似的长方形计算面积, 圆柱可以转化成近似的长方体计算体积吗?
探索与发现
探索与发现
探索与发现
探索与发现
平均分的份数越多, 拼成的
物体就越接近长方体。
如果把圆柱的底面平均分成32 份、64 份……切开后拼成的物体会有什么变化?
拼成了一个近
似的长方体。
探索与发现
拼成的长方体与原来的圆柱有什么关系?
长方体的体积与圆柱的体积相等。
长方体的高等于
圆柱的高。
长方体的底面积等于圆柱的底面积。
探索与发现
长方体的体积= 底面积 × 高
圆柱体的体积=
高
×
底面积
高
底面积
高
V=sh=πr2h
探索与发现
底面积相等、高也相等的长方体、正方体和圆柱的体积相等。推导出圆柱的体积计算公式是:圆柱的体积=底面积×高,用字母表示是V=Sh(V表示体积,S表示底面积,h表示高)。
探索与发现
可以用长方体体
积公式推导出圆
柱体积公式。
计算长方体、正方体、圆柱的体积都可以用底面积乘高。
把圆柱转化成长方
体, 与探索圆面积
的方法类似。
回顾圆柱体积公式的探索过
程, 你有什么体会?
探索与发现
探索与发现
探索与发现
学以致用
03
学以致用
1.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m3。这根木料最多能做多少张桌椅?
学以致用
3.14×(0.4÷2)2×5÷0.02
=31.4≈31(张)
学以致用
2.一个圆柱的体积是80cm3,底面积是16cm2。它的高是多少厘米?
80÷16=5(cm)
学以致用
3.把一个长15.7cm、宽12cm、高5cm的长方体铁块熔铸成一根底面半径是2cm的圆柱形铁棍,铁棍的长是多少厘米?
15.7×12×5÷(3.14×2 )=75(cm)
课后作业
04
完成教材课后习题及练习册同步练习。
课后作业
感 谢 观 看
六年级数学下册教学课件(苏教版)
第二单元 圆柱和圆锥
第三课时 圆柱的体积
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
我们在推导圆的面积公式时,是把它转化成近似的长方形,找到这个长方形与圆各部分之间的联系,由长方形的面积公式推导出了圆的面积公式。
探索与发现
02
探索与发现
探索与发现
今天,我们能不能也用这个思路研究圆柱体积的计算问题呢?
探索与发现
下面的长方体、正方体和圆柱的底面积相等,高也相等。
(1)长方体与正方体的体积相等吗?为什么?
(2)猜一猜,圆柱的体积与长方体、正方体的体积相等吗?用什么办法验证呢?
探索与发现
探索与发现
圆可以转化成近似的长方形计算面积, 圆柱可以转化成近似的长方体计算体积吗?
探索与发现
探索与发现
探索与发现
探索与发现
平均分的份数越多, 拼成的
物体就越接近长方体。
如果把圆柱的底面平均分成32 份、64 份……切开后拼成的物体会有什么变化?
拼成了一个近
似的长方体。
探索与发现
拼成的长方体与原来的圆柱有什么关系?
长方体的体积与圆柱的体积相等。
长方体的高等于
圆柱的高。
长方体的底面积等于圆柱的底面积。
探索与发现
长方体的体积= 底面积 × 高
圆柱体的体积=
高
×
底面积
高
底面积
高
V=sh=πr2h
探索与发现
底面积相等、高也相等的长方体、正方体和圆柱的体积相等。推导出圆柱的体积计算公式是:圆柱的体积=底面积×高,用字母表示是V=Sh(V表示体积,S表示底面积,h表示高)。
探索与发现
可以用长方体体
积公式推导出圆
柱体积公式。
计算长方体、正方体、圆柱的体积都可以用底面积乘高。
把圆柱转化成长方
体, 与探索圆面积
的方法类似。
回顾圆柱体积公式的探索过
程, 你有什么体会?
探索与发现
探索与发现
探索与发现
学以致用
03
学以致用
1.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m3。这根木料最多能做多少张桌椅?
学以致用
3.14×(0.4÷2)2×5÷0.02
=31.4≈31(张)
学以致用
2.一个圆柱的体积是80cm3,底面积是16cm2。它的高是多少厘米?
80÷16=5(cm)
学以致用
3.把一个长15.7cm、宽12cm、高5cm的长方体铁块熔铸成一根底面半径是2cm的圆柱形铁棍,铁棍的长是多少厘米?
15.7×12×5÷(3.14×2 )=75(cm)
课后作业
04
完成教材课后习题及练习册同步练习。
课后作业
感 谢 观 看
