数学人教A版(2019)选择性必修第三册8.2.1一元线性回归模型 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.2.1一元线性回归模型 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 11:33:40 | ||
图片预览





文档简介
(共15张PPT)
8.2.1 一元线性回归模型
8.2 一元线性回归模型及其应用
情 境 导 入
通过前面的学习我们已经知道,根据成对样本数据的散点图和相关系数,可以判断两个变量是否存在相关关系、是正相关还是负相关,以及线性相关程度的强弱等.
思考:如何建立适当的统计模型来刻画两个变量之间的相关关系?并通过模型进行预测?
问题情境:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
思考:
你觉得,儿子身高与父亲身高的关系怎样呢?
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
由图可知散点大致分布在一条从左下角到右,上角的直线附近,表明儿子身高和父亲身高线性相关.
一、散点图
二、样本相关系数
,表明儿子身高和父亲身高正线性相关,且相关程度较高.
r≈0.886
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
随机误差e的特征
随机误差e是一个随机变量
①可取正或取负
②有些无法测量
③不可事先设定
对于任意一组(xi,Yi),都有一个ei与之对应
ei是个随机变量
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
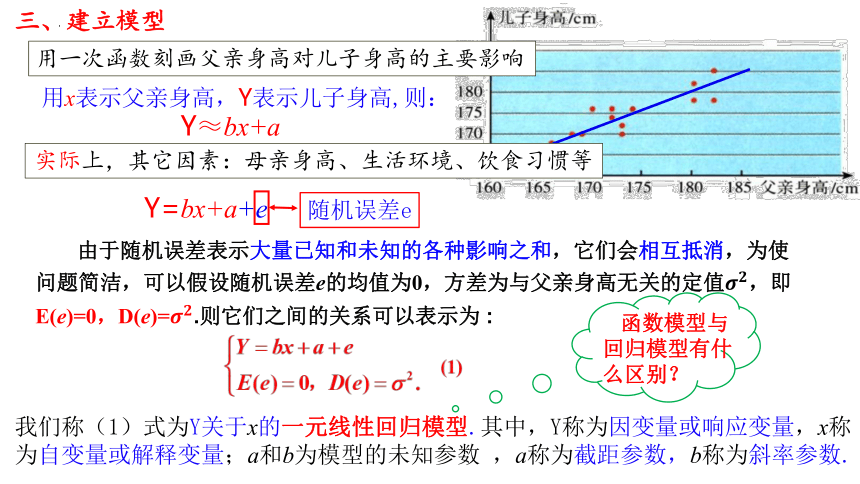
由于随机误差表示大量已知和未知的各种影响之和,它们会相互抵消,为使问题简洁,可以假设随机误差e的均值为0,方差为与父亲身高无关的定值,即E(e)=0,D(e)=.则它们之间的关系可以表示为 :
我们称(1)式为Y关于x的一元线性回归模型.其中,Y称为因变量或响应变量,x称为自变量或解释变量;a和b为模型的未知参数 ,a称为截距参数,b称为斜率参数.
函数模型与回归模型有什么区别?
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
函数模型与回归模型有什么区别?
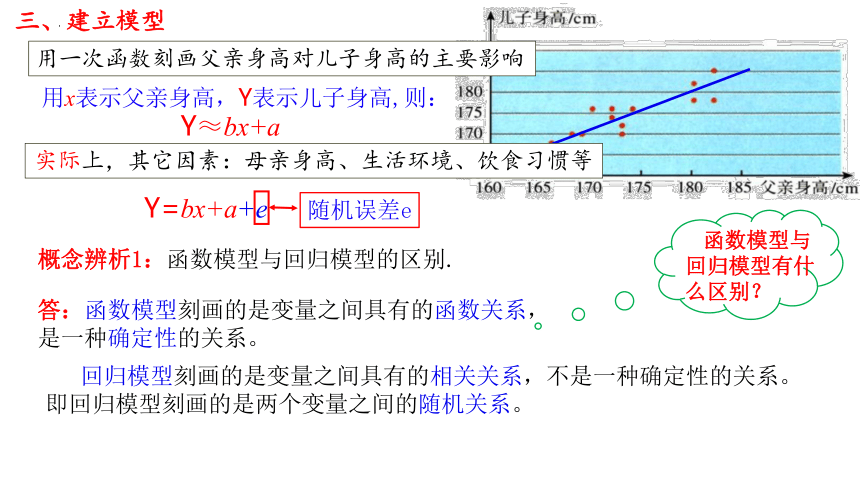
概念辨析1:函数模型与回归模型的区别.
答:函数模型刻画的是变量之间具有的函数关系,是一种确定性的关系。
回归模型刻画的是变量之间具有的相关关系,不是一种确定性的关系。
即回归模型刻画的是两个变量之间的随机关系。
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
概念辨析2:在一元线性回归模型(1)中,参数b的含义是什么?
答:自变量x每增加个单位,
响应变量Y的均值将增加b个单位。
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
概念辨析3:进一步结合实例解释产生模型(1)中随机误差的原因?
答:
随机误差e的来源(可以推广到一般):
1、忽略了其它因素的影响:影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差。
以上三项误差越小,说明我们的回归模型的拟合效果越好。
根据此原理,我们尝试推导出拟合效果最好的一元线性回归方程
例题1 若某地财政收入x与支出y满足一元线性回归模型y=bx+a+e(单元:亿元),其中b=0.7,a=3,|e|≤0.5,如果今年该地区财政收入10亿元,年支出预计不会超过多少?
解:因为财政收入x与支出y满足一元线性回归模型y=bx+a+e,
其中b=0.7,a=3,所以得到 y=0.7 x+3+e,
当 x=10时,得 y=0.7×10+3+e=10+e,
而|e|≤0.5,即-0.5≤e≤0.5,所以9.5≤y≤10.5,
所以年支出预计不会超过10.5亿元.
例题2 某种新产品表面需要腐蚀刻线,腐蚀深度Y(μm)与腐蚀时间x(s)有关,测得结果如下:
(1) 请根据以上数据判断,腐蚀深度Y(μm)与腐蚀时间x(s)之间的关系能否用一元线性回归模型,来刻画?并说明理由。
(2) 请说明模型中分别表示什么?本题中的具体含义是什么?
2.建立一元线性回归模型的步骤
1.一元线性回归模型
(1)与函数模型的区别
(2)随机误差产生的原因及分布
定性分析
定量分析
函数关系 or 相关关系 or 没有关系?
课堂小结
(1)整理数据
课本107页
1. 说明函数模型与回归模型的区别,并分别举出两个应用函数模型和回归模型的例子.
解:函数模型刻画的是变量之间具有的函数关系,是一种确定性的关系.回归模型刻画的是变量之间具有的相关关系,不是一种确定性的关系,即回归模型刻画的是两个变量之间的随机关系.
例如,路程与速度的关系、正方体体积与边长的关系可以应用函数模型刻画;体重与身高的关系、冷饮销量与气温的关系可以应用回归模型刻画.
课本107页
2. 在一元线性回归模型(1) 中,参数b的含义是什么
解:参数b的含义可以解释为解释变量x对响应变量Y的均值的影响,变量x每增加1个单位,响应变量Y的均值将增加b个单位.
例如,教科书中父亲身高为175 cm的儿子身高的均值比父亲身高为174cm的儿子身高的均值高出0.839cm.
注意:因为响应变量Y最终取值,除了受变量x的影响,还要受随机误差e的影响,所以不能解释成解释变量x每增加一个单位,响应变量Y增加b个单位.
解:不能.
一是父亲的身高与儿子的身高之间是随机关系,不是函数关系;
二是这组数据仅是总体的一个样本,不一定能很好地描述两个变量之间的关系.
课本107页
3. 将图8.2-1中的点按父亲身高的大小次序用折线连起来,所得到的图象是一个折线图,可以用这条折线表示儿子身高和父亲身高之间的关系吗?
8.2.1 一元线性回归模型
8.2 一元线性回归模型及其应用
情 境 导 入
通过前面的学习我们已经知道,根据成对样本数据的散点图和相关系数,可以判断两个变量是否存在相关关系、是正相关还是负相关,以及线性相关程度的强弱等.
思考:如何建立适当的统计模型来刻画两个变量之间的相关关系?并通过模型进行预测?
问题情境:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
思考:
你觉得,儿子身高与父亲身高的关系怎样呢?
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
由图可知散点大致分布在一条从左下角到右,上角的直线附近,表明儿子身高和父亲身高线性相关.
一、散点图
二、样本相关系数
,表明儿子身高和父亲身高正线性相关,且相关程度较高.
r≈0.886
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
随机误差e的特征
随机误差e是一个随机变量
①可取正或取负
②有些无法测量
③不可事先设定
对于任意一组(xi,Yi),都有一个ei与之对应
ei是个随机变量
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
由于随机误差表示大量已知和未知的各种影响之和,它们会相互抵消,为使问题简洁,可以假设随机误差e的均值为0,方差为与父亲身高无关的定值,即E(e)=0,D(e)=.则它们之间的关系可以表示为 :
我们称(1)式为Y关于x的一元线性回归模型.其中,Y称为因变量或响应变量,x称为自变量或解释变量;a和b为模型的未知参数 ,a称为截距参数,b称为斜率参数.
函数模型与回归模型有什么区别?
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
函数模型与回归模型有什么区别?
概念辨析1:函数模型与回归模型的区别.
答:函数模型刻画的是变量之间具有的函数关系,是一种确定性的关系。
回归模型刻画的是变量之间具有的相关关系,不是一种确定性的关系。
即回归模型刻画的是两个变量之间的随机关系。
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
概念辨析2:在一元线性回归模型(1)中,参数b的含义是什么?
答:自变量x每增加个单位,
响应变量Y的均值将增加b个单位。
三、建立模型
用x表示父亲身高,Y表示儿子身高,则:
用一次函数刻画父亲身高对儿子身高的主要影响
Y=bx+a+e
实际上,其它因素:母亲身高、生活环境、饮食习惯等
随机误差e
Y≈bx+a
概念辨析3:进一步结合实例解释产生模型(1)中随机误差的原因?
答:
随机误差e的来源(可以推广到一般):
1、忽略了其它因素的影响:影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差。
以上三项误差越小,说明我们的回归模型的拟合效果越好。
根据此原理,我们尝试推导出拟合效果最好的一元线性回归方程
例题1 若某地财政收入x与支出y满足一元线性回归模型y=bx+a+e(单元:亿元),其中b=0.7,a=3,|e|≤0.5,如果今年该地区财政收入10亿元,年支出预计不会超过多少?
解:因为财政收入x与支出y满足一元线性回归模型y=bx+a+e,
其中b=0.7,a=3,所以得到 y=0.7 x+3+e,
当 x=10时,得 y=0.7×10+3+e=10+e,
而|e|≤0.5,即-0.5≤e≤0.5,所以9.5≤y≤10.5,
所以年支出预计不会超过10.5亿元.
例题2 某种新产品表面需要腐蚀刻线,腐蚀深度Y(μm)与腐蚀时间x(s)有关,测得结果如下:
(1) 请根据以上数据判断,腐蚀深度Y(μm)与腐蚀时间x(s)之间的关系能否用一元线性回归模型,来刻画?并说明理由。
(2) 请说明模型中分别表示什么?本题中的具体含义是什么?
2.建立一元线性回归模型的步骤
1.一元线性回归模型
(1)与函数模型的区别
(2)随机误差产生的原因及分布
定性分析
定量分析
函数关系 or 相关关系 or 没有关系?
课堂小结
(1)整理数据
课本107页
1. 说明函数模型与回归模型的区别,并分别举出两个应用函数模型和回归模型的例子.
解:函数模型刻画的是变量之间具有的函数关系,是一种确定性的关系.回归模型刻画的是变量之间具有的相关关系,不是一种确定性的关系,即回归模型刻画的是两个变量之间的随机关系.
例如,路程与速度的关系、正方体体积与边长的关系可以应用函数模型刻画;体重与身高的关系、冷饮销量与气温的关系可以应用回归模型刻画.
课本107页
2. 在一元线性回归模型(1) 中,参数b的含义是什么
解:参数b的含义可以解释为解释变量x对响应变量Y的均值的影响,变量x每增加1个单位,响应变量Y的均值将增加b个单位.
例如,教科书中父亲身高为175 cm的儿子身高的均值比父亲身高为174cm的儿子身高的均值高出0.839cm.
注意:因为响应变量Y最终取值,除了受变量x的影响,还要受随机误差e的影响,所以不能解释成解释变量x每增加一个单位,响应变量Y增加b个单位.
解:不能.
一是父亲的身高与儿子的身高之间是随机关系,不是函数关系;
二是这组数据仅是总体的一个样本,不一定能很好地描述两个变量之间的关系.
课本107页
3. 将图8.2-1中的点按父亲身高的大小次序用折线连起来,所得到的图象是一个折线图,可以用这条折线表示儿子身高和父亲身高之间的关系吗?
