北师大版数学必修第2册第6章 立体几何初步 综合检测题(原卷版+解析版)
文档属性
| 名称 | 北师大版数学必修第2册第6章 立体几何初步 综合检测题(原卷版+解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 11:34:21 | ||
图片预览




文档简介
第六章 立体几何初步
综合检测题(原卷版)
考试时间120分钟,满分150分.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列命题:
①在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中真命题的个数是( )
A.0 B.1
C.2 D.3
2.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( )
A.64π cm2 B.36π cm2
C.64π cm2或36π cm2 D.48π cm2
3.梯形ABCD中,AB∥CD,AB 平面α,CD平面α,则直线CD与平面α内的直线的位置关系只能是( )
A.平行 B.平行或异面
C.平行或相交 D.异面或相交
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
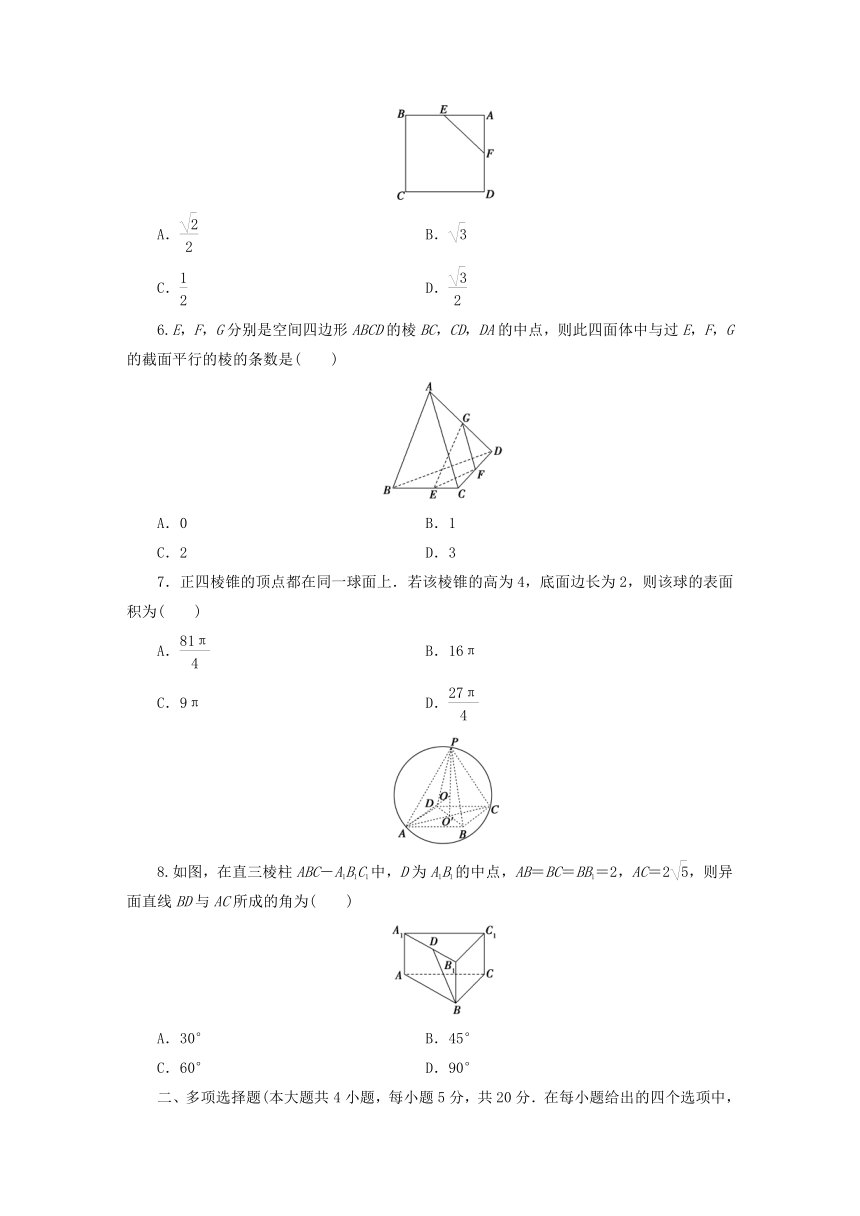
5.如图所示,正方形ABCD中,E,F分别是AB,AD的中点,将此正方形沿EF折成直二面角后,异面直线AF与BE所成角的余弦值为( )
A. B.
C. D.
6.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( )
A.0 B.1
C.2 D.3
7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π
C.9π D.
8.如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=BB1=2,AC=2,则异面直线BD与AC所成的角为( )
A.30° B.45°
C.60° D.90°
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
10.如图,在平行六面体ABCD -A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则下列说法正确的是( )
A.A1M∥D1P B.A1M∥B1Q
C.A1M∥平面DCC1D1 D.A1M∥平面D1PQB1
11.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,一定正确的为( )
A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°
12.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则( )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是 .
14.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为 厘米.
15.已知a,b表示直线,α,β,γ表示平面.
①若α∩β=a,b α,a⊥b,则α⊥β;②若a α,a垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a,α∩γ=b,则a⊥b;④若a⊥α,b⊥β,a∥b,则α∥β.
上述命题中,正确命题的序号是 .
16.如图,在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E,F是PA和AB的中点,则PA= 2 ,PA与平面PBC所成角的正弦值为 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.
18.(本小题满分12分)如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
(1)若CD∥平面PBO,试指出点O的位置;
(2)求证:平面PAB⊥平面PCD.
19.(本小题满分12分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
20.(本小题满分12分)如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,CD⊥PA,DB平分∠ADC,E为PC的中点,∠DAC=45°,AC=.
(1)求证:PA∥平面BDE;
(2)若PD=2,BD=2,求四棱锥E-ABCD的体积.
21.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于D,E,又SA=AB,SB=BC.
(1)求证:BD⊥平面SAC;
(2)求二面角E-BD-C的大小.
22.(本小题满分12分)已知梯形BFEC如图1所示,其中BF∥EC,EC=3,BF=2,四边形ABCD是边长为1的正方形,沿AD将四边形EDAF折起,使得平面EDAF⊥平面ABCD,得到如图2所示的几何体.
(1)求证:平面AEC⊥平面BDE;
(2)求点F到平面ABE的距离.
第六章 立体几何初步
综合检测题(解析版)
考试时间120分钟,满分150分.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列命题:
①在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中真命题的个数是( A )
A.0 B.1
C.2 D.3
[解析]
①不一定,只有当这两点的连线与圆台的轴共面时,才是母线;②不一定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,如图所示;③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.
2.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( C )
A.64π cm2 B.36π cm2
C.64π cm2或36π cm2 D.48π cm2
[解析] 分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,即可得到两种不同大小的圆柱,显然C选项正确.
3.梯形ABCD中,AB∥CD,AB 平面α,CD平面α,则直线CD与平面α内的直线的位置关系只能是( B )
A.平行 B.平行或异面
C.平行或相交 D.异面或相交
[解析] 由直线与平面平行的判定定理,可知CD∥α,所以CD与平面α内的直线没有公共点.
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( D )
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
[解析] 连接DC1,可知MN是△C1DB的中位线,所以MN∥BD,BD与A1B1不平行,所以MN不可能与A1B1平行.
5.如图所示,正方形ABCD中,E,F分别是AB,AD的中点,将此正方形沿EF折成直二面角后,异面直线AF与BE所成角的余弦值为( C )
A. B.
C. D.
[解析] 过点F作FH∥DC,交BC于H,过点A作AG⊥EF,交EF于G,连接GH,AH,则∠AFH(或其补角)为异面直线AF与BE所成的角.设正方形ABCD的边长为2,在△AGH中,AH==,在△AFH中,AF=1,FH=2,AH=,∴cos ∠AFH=.
6.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( C )
A.0 B.1
C.2 D.3
[解析] 在△ACD中,∵G,F分别为AD与CD的中点,∴GF∥AC.而GF 平面EFG,AC平面EFG,∴AC∥平面EFG.同理,BD∥平面EFG.故选C.
7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )
A. B.16π
C.9π D.
[解析] 如图所示,设球的半径为R,球心为O,正四棱锥的底面中心为O′.∵正四棱锥P-ABCD中AB=2,
∴AO′=.∵PO′=4,
∴在Rt△AOO′中,AO2=AO′2+OO′2,∴R2=()2+(4-R)2,解得R=,∴该球的表面积为4πR2=4π×2=,故选A.
8.如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=BB1=2,AC=2,则异面直线BD与AC所成的角为( C )
A.30° B.45°
C.60° D.90°
[解析] 如图,取B1C1的中点E,连接BE,DE,则AC∥A1C1∥DE,则∠BDE即为异面直线BD与AC所成的角.由条件可知BD=DE=EB=,所以∠BDE=60°,故选C.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列命题为真命题的是( BD )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
[解析] A错,两个平面相交时,也有无数个公共点;C错,比如a⊥α,b α,c α,显然有a⊥b,a⊥c,但b与c也可能相交.故选BD.
10.如图,在平行六面体ABCD -A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则下列说法正确的是( ACD )
A.A1M∥D1P B.A1M∥B1Q
C.A1M∥平面DCC1D1 D.A1M∥平面D1PQB1
[解析] 连接PM,因为M、P为AB、CD的中点,故PM平行且等于AD.由题意知AD平行且等于A1D1,故PM平行且等于A1D1,所以四边形PMA1D1为平行四边形,所以A1M∥D1P.故A正确;显然A1M与B1Q为异面直线,故B错误;由A知A1M∥D1P,由于D1P既在平面DCC1D1内,又在平面D1PQB1内,且A1M即不在平面DCC1D1内,又不在平面D1PQB1内,故C、D正确.故选ACD.
11.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,一定正确的为( ABD )
A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°
[解析] ∵QM∥PN,∴QM∥平面ABD,∴QM∥BD,同理可得AC∥MN,∵QM∥BD,AC∥MN,MN⊥QM,∴AC⊥BD,A正确;∵AC∥MN,∴AC∥截面PQMN,B正确;∵QM∥BD,AC∥MN,∴+=1,C不一定正确;∵QM∥BD,∴异面直线PM与BD所成的角为∠PMQ=45°,D正确.故选ABD.
12.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则( BC )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
[解析] 取DD1中点M,则AM为AF在平面AA1D1D上的射影,∵AM与DD1不垂直,∴AF与DD1不垂直,故A选项错误;∵A1G∥D1F,A1G平面AEFD1,∴A1G∥平面AEFD1,故B选项正确;平面AEF截正方体所得截面为等腰梯形AEFD1,易知梯形面积为,故C选项正确;
假设C与G到平面AEF的距离相等,即平面AEF将CG平分,则平面AEF必过CG中点,连接CG交EF于H,而H不是CG中点,则假设不成立.故D选项错误.故选BC.
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是 .
[解析] ∵圆柱的侧面展开图是边长为1的正方形,
∴该圆柱的高h=1,底面周长2πr=1,∴底面半径r=,
∴该圆柱的体积V=π××1=.
14.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为 12 厘米.
[解析] V=Sh=πr2h=πR3,
R==12(厘米).
15.已知a,b表示直线,α,β,γ表示平面.
①若α∩β=a,b α,a⊥b,则α⊥β;②若a α,a垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a,α∩γ=b,则a⊥b;④若a⊥α,b⊥β,a∥b,则α∥β.
上述命题中,正确命题的序号是 ②④ .
[解析] 对①可举反例,如图,需b⊥β才能推出α⊥β;对③可举反例说明,当γ不与α,β的交线垂直时,即可知a,b不垂直;根据面面、线面垂直的定义与判定知②④正确.
16.如图,在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E,F是PA和AB的中点,则PA= 2 ,PA与平面PBC所成角的正弦值为 .
[解析] 如图所示,连接AC,过A作AH⊥BC于H,连接PH,
∵PC⊥平面ABCD,AH 平面ABCD,
∴PC⊥AH,
又PC∩BC=C,
∴AH⊥平面PBC,
∴∠APH为PA与平面PBC所成的角,在边长为2的菱形ABCD中,∠ABC=60°,
∴△ABC为正三角形,
又AH⊥BC,∴H为BC中点,AH=,
∵PC=AC=2,∴PA=2,
∴sin∠APH==.故PA与平面PBC所成角的正弦值为.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.
[解析] 不会溢出杯子.理由如下:由题图可知半球的半径为4 cm,所以V半球=×πR3=×π×43=π(cm3),V圆锥=πr2h=π×42×12=64π(cm3).
因为V半球18.(本小题满分12分)如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
(1)若CD∥平面PBO,试指出点O的位置;
(2)求证:平面PAB⊥平面PCD.
[解析] (1)∵CD∥平面PBO,CD 平面ABCD,
且平面ABCD∩平面PBO=BO,
∴BO∥CD.
又BC∥AD,∴四边形BCDO为平行四边形,
则BC=DO,而AD=3BC,
∴AD=3OD,即点O是靠近点D的线段AD的一个三等分点.
(2)证明:∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,AB 底面ABCD,且AB⊥AD,
∴AB⊥平面PAD.
又PD 平面PAD,∴AB⊥PD.又PA⊥PD,
AB∩PA=A,AB,PA 平面PAB,∴PD⊥平面PAB.
又PD 平面PCD,∴平面PAB⊥平面PCD.
19.(本小题满分12分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
[解析] (1)因为E,F分别是AC,B1C的中点,所以EF∥AB1.
又EF平面AB1C1,AB1 平面AB1C1,
所以EF∥平面AB1C1.
(2)因为B1C⊥平面ABC,AB 平面ABC,
所以B1C⊥AB.
又AB⊥AC,B1C 平面AB1C,AC 平面AB1C,B1C∩AC=C,
所以AB⊥平面AB1C.
又因为AB 平面ABB1,所以平面AB1C⊥平面ABB1.
20.(本小题满分12分)如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,CD⊥PA,DB平分∠ADC,E为PC的中点,∠DAC=45°,AC=.
(1)求证:PA∥平面BDE;
(2)若PD=2,BD=2,求四棱锥E-ABCD的体积.
[解析] (1)设AC∩BD=F,连接EF.
∵PD⊥平面ABCD,CD 平面ABCD,∴PD⊥CD.
∵CD⊥PA,PA∩PD=P,∴CD⊥平面PAD.
∵AD 平面PAD,∴CD⊥AD.
∵∠DAC=45°,∴DA=DC.
∵DB平分∠ADC,∴F为AC的中点.
∵E为PC的中点,∴EF为△CPA的中位线,∴EF∥PA.
又EF 平面BDE,PA平面BDE,∴PA∥平面BDE.
(2)由(1)知DB⊥AC,将底面四边形ABCD的面积记为S,则S=S△ADC+S△ABC=××+××=2.
∵点E为线段PC的中点,
∴V四棱锥E-ABCD=S×PD=×2××2=.
21.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于D,E,又SA=AB,SB=BC.
(1)求证:BD⊥平面SAC;
(2)求二面角E-BD-C的大小.
[解析]
(1)证明:如图,
∵DE⊥SC,且E为SC的中点,又SB=BC,
∴BE⊥SC.
又DE∩BE=E,
根据直线与平面垂直的判定定理知SC⊥平面BDE,
∵BD 平面BDE,∴SC⊥BD.
又SA⊥平面ABC,BD 平面ABC,∴SA⊥BD.
又SA∩SC=S,∴BD⊥平面SAC.
(2)由(1)知∠EDC为二面角E-BD-C的平面角,又△SAC∽△DEC,∴∠EDC=∠ASC.
在Rt△SAB中,∠SAB=90°,
设SA=AB=1,则SB=.
由SA⊥BC,AB⊥BC,AB∩SA=A,
∴BC⊥平面SAB,SB 平面SAB,∴BC⊥SB.
在Rt△SBC中,SB=BC=,∠SBC=90°,则SC=2.
在Rt△SAC中,∠SAC=90°,SA=1,SC=2.
∴cos ∠ASC==,
∴∠ASC=60°,即二面角E-BD-C的大小为60°.
22.(本小题满分12分)已知梯形BFEC如图1所示,其中BF∥EC,EC=3,BF=2,四边形ABCD是边长为1的正方形,沿AD将四边形EDAF折起,使得平面EDAF⊥平面ABCD,得到如图2所示的几何体.
(1)求证:平面AEC⊥平面BDE;
(2)求点F到平面ABE的距离.
[解析] (1)∵平面EDAF⊥平面ABCD,DE 平面EDAF.
平面EDAF∩平面ABCD=AD,DE⊥AD,∴DE⊥平面ABCD,
∵AC 平面ABCD,∴DE⊥AC,
∵四边形ABCD是正方形,∴AC⊥BD
∵DE、BD 平面BDE,DE∩BD=D,∴AC⊥平面BDE,
∵AC 平面ACE,∴平面AEC⊥平面BDE.
(2)过点F作FG⊥AE于点G,
因为平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
AB 平面ABCD,AB⊥AD,
所以AB⊥平面ADEF,又FG 平面ADEF,所以AB⊥FG,
又AB∩AE=A,AB,AE 平面ABE,所以FG⊥平面ABE,
所以线段FG的长即为点F到平面ABE的距离,
AF=1,AE=,
S△AEF=×1×1=,S△ABE=×1×=,
由VB-AEF=VF-ABE,得S△ABE·FG=S△AEF·AB,即FG=,
所以FG=,
即点F到平面ABE的距离为.
综合检测题(原卷版)
考试时间120分钟,满分150分.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列命题:
①在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中真命题的个数是( )
A.0 B.1
C.2 D.3
2.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( )
A.64π cm2 B.36π cm2
C.64π cm2或36π cm2 D.48π cm2
3.梯形ABCD中,AB∥CD,AB 平面α,CD平面α,则直线CD与平面α内的直线的位置关系只能是( )
A.平行 B.平行或异面
C.平行或相交 D.异面或相交
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
5.如图所示,正方形ABCD中,E,F分别是AB,AD的中点,将此正方形沿EF折成直二面角后,异面直线AF与BE所成角的余弦值为( )
A. B.
C. D.
6.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( )
A.0 B.1
C.2 D.3
7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π
C.9π D.
8.如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=BB1=2,AC=2,则异面直线BD与AC所成的角为( )
A.30° B.45°
C.60° D.90°
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
10.如图,在平行六面体ABCD -A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则下列说法正确的是( )
A.A1M∥D1P B.A1M∥B1Q
C.A1M∥平面DCC1D1 D.A1M∥平面D1PQB1
11.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,一定正确的为( )
A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°
12.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则( )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是 .
14.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为 厘米.
15.已知a,b表示直线,α,β,γ表示平面.
①若α∩β=a,b α,a⊥b,则α⊥β;②若a α,a垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a,α∩γ=b,则a⊥b;④若a⊥α,b⊥β,a∥b,则α∥β.
上述命题中,正确命题的序号是 .
16.如图,在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E,F是PA和AB的中点,则PA= 2 ,PA与平面PBC所成角的正弦值为 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.
18.(本小题满分12分)如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
(1)若CD∥平面PBO,试指出点O的位置;
(2)求证:平面PAB⊥平面PCD.
19.(本小题满分12分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
20.(本小题满分12分)如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,CD⊥PA,DB平分∠ADC,E为PC的中点,∠DAC=45°,AC=.
(1)求证:PA∥平面BDE;
(2)若PD=2,BD=2,求四棱锥E-ABCD的体积.
21.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于D,E,又SA=AB,SB=BC.
(1)求证:BD⊥平面SAC;
(2)求二面角E-BD-C的大小.
22.(本小题满分12分)已知梯形BFEC如图1所示,其中BF∥EC,EC=3,BF=2,四边形ABCD是边长为1的正方形,沿AD将四边形EDAF折起,使得平面EDAF⊥平面ABCD,得到如图2所示的几何体.
(1)求证:平面AEC⊥平面BDE;
(2)求点F到平面ABE的距离.
第六章 立体几何初步
综合检测题(解析版)
考试时间120分钟,满分150分.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列命题:
①在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中真命题的个数是( A )
A.0 B.1
C.2 D.3
[解析]
①不一定,只有当这两点的连线与圆台的轴共面时,才是母线;②不一定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,如图所示;③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.
2.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( C )
A.64π cm2 B.36π cm2
C.64π cm2或36π cm2 D.48π cm2
[解析] 分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,即可得到两种不同大小的圆柱,显然C选项正确.
3.梯形ABCD中,AB∥CD,AB 平面α,CD平面α,则直线CD与平面α内的直线的位置关系只能是( B )
A.平行 B.平行或异面
C.平行或相交 D.异面或相交
[解析] 由直线与平面平行的判定定理,可知CD∥α,所以CD与平面α内的直线没有公共点.
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( D )
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
[解析] 连接DC1,可知MN是△C1DB的中位线,所以MN∥BD,BD与A1B1不平行,所以MN不可能与A1B1平行.
5.如图所示,正方形ABCD中,E,F分别是AB,AD的中点,将此正方形沿EF折成直二面角后,异面直线AF与BE所成角的余弦值为( C )
A. B.
C. D.
[解析] 过点F作FH∥DC,交BC于H,过点A作AG⊥EF,交EF于G,连接GH,AH,则∠AFH(或其补角)为异面直线AF与BE所成的角.设正方形ABCD的边长为2,在△AGH中,AH==,在△AFH中,AF=1,FH=2,AH=,∴cos ∠AFH=.
6.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( C )
A.0 B.1
C.2 D.3
[解析] 在△ACD中,∵G,F分别为AD与CD的中点,∴GF∥AC.而GF 平面EFG,AC平面EFG,∴AC∥平面EFG.同理,BD∥平面EFG.故选C.
7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )
A. B.16π
C.9π D.
[解析] 如图所示,设球的半径为R,球心为O,正四棱锥的底面中心为O′.∵正四棱锥P-ABCD中AB=2,
∴AO′=.∵PO′=4,
∴在Rt△AOO′中,AO2=AO′2+OO′2,∴R2=()2+(4-R)2,解得R=,∴该球的表面积为4πR2=4π×2=,故选A.
8.如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=BB1=2,AC=2,则异面直线BD与AC所成的角为( C )
A.30° B.45°
C.60° D.90°
[解析] 如图,取B1C1的中点E,连接BE,DE,则AC∥A1C1∥DE,则∠BDE即为异面直线BD与AC所成的角.由条件可知BD=DE=EB=,所以∠BDE=60°,故选C.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列命题为真命题的是( BD )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
[解析] A错,两个平面相交时,也有无数个公共点;C错,比如a⊥α,b α,c α,显然有a⊥b,a⊥c,但b与c也可能相交.故选BD.
10.如图,在平行六面体ABCD -A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则下列说法正确的是( ACD )
A.A1M∥D1P B.A1M∥B1Q
C.A1M∥平面DCC1D1 D.A1M∥平面D1PQB1
[解析] 连接PM,因为M、P为AB、CD的中点,故PM平行且等于AD.由题意知AD平行且等于A1D1,故PM平行且等于A1D1,所以四边形PMA1D1为平行四边形,所以A1M∥D1P.故A正确;显然A1M与B1Q为异面直线,故B错误;由A知A1M∥D1P,由于D1P既在平面DCC1D1内,又在平面D1PQB1内,且A1M即不在平面DCC1D1内,又不在平面D1PQB1内,故C、D正确.故选ACD.
11.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,一定正确的为( ABD )
A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°
[解析] ∵QM∥PN,∴QM∥平面ABD,∴QM∥BD,同理可得AC∥MN,∵QM∥BD,AC∥MN,MN⊥QM,∴AC⊥BD,A正确;∵AC∥MN,∴AC∥截面PQMN,B正确;∵QM∥BD,AC∥MN,∴+=1,C不一定正确;∵QM∥BD,∴异面直线PM与BD所成的角为∠PMQ=45°,D正确.故选ABD.
12.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则( BC )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
[解析] 取DD1中点M,则AM为AF在平面AA1D1D上的射影,∵AM与DD1不垂直,∴AF与DD1不垂直,故A选项错误;∵A1G∥D1F,A1G平面AEFD1,∴A1G∥平面AEFD1,故B选项正确;平面AEF截正方体所得截面为等腰梯形AEFD1,易知梯形面积为,故C选项正确;
假设C与G到平面AEF的距离相等,即平面AEF将CG平分,则平面AEF必过CG中点,连接CG交EF于H,而H不是CG中点,则假设不成立.故D选项错误.故选BC.
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是 .
[解析] ∵圆柱的侧面展开图是边长为1的正方形,
∴该圆柱的高h=1,底面周长2πr=1,∴底面半径r=,
∴该圆柱的体积V=π××1=.
14.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为 12 厘米.
[解析] V=Sh=πr2h=πR3,
R==12(厘米).
15.已知a,b表示直线,α,β,γ表示平面.
①若α∩β=a,b α,a⊥b,则α⊥β;②若a α,a垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a,α∩γ=b,则a⊥b;④若a⊥α,b⊥β,a∥b,则α∥β.
上述命题中,正确命题的序号是 ②④ .
[解析] 对①可举反例,如图,需b⊥β才能推出α⊥β;对③可举反例说明,当γ不与α,β的交线垂直时,即可知a,b不垂直;根据面面、线面垂直的定义与判定知②④正确.
16.如图,在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E,F是PA和AB的中点,则PA= 2 ,PA与平面PBC所成角的正弦值为 .
[解析] 如图所示,连接AC,过A作AH⊥BC于H,连接PH,
∵PC⊥平面ABCD,AH 平面ABCD,
∴PC⊥AH,
又PC∩BC=C,
∴AH⊥平面PBC,
∴∠APH为PA与平面PBC所成的角,在边长为2的菱形ABCD中,∠ABC=60°,
∴△ABC为正三角形,
又AH⊥BC,∴H为BC中点,AH=,
∵PC=AC=2,∴PA=2,
∴sin∠APH==.故PA与平面PBC所成角的正弦值为.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.
[解析] 不会溢出杯子.理由如下:由题图可知半球的半径为4 cm,所以V半球=×πR3=×π×43=π(cm3),V圆锥=πr2h=π×42×12=64π(cm3).
因为V半球
(1)若CD∥平面PBO,试指出点O的位置;
(2)求证:平面PAB⊥平面PCD.
[解析] (1)∵CD∥平面PBO,CD 平面ABCD,
且平面ABCD∩平面PBO=BO,
∴BO∥CD.
又BC∥AD,∴四边形BCDO为平行四边形,
则BC=DO,而AD=3BC,
∴AD=3OD,即点O是靠近点D的线段AD的一个三等分点.
(2)证明:∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,AB 底面ABCD,且AB⊥AD,
∴AB⊥平面PAD.
又PD 平面PAD,∴AB⊥PD.又PA⊥PD,
AB∩PA=A,AB,PA 平面PAB,∴PD⊥平面PAB.
又PD 平面PCD,∴平面PAB⊥平面PCD.
19.(本小题满分12分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
[解析] (1)因为E,F分别是AC,B1C的中点,所以EF∥AB1.
又EF平面AB1C1,AB1 平面AB1C1,
所以EF∥平面AB1C1.
(2)因为B1C⊥平面ABC,AB 平面ABC,
所以B1C⊥AB.
又AB⊥AC,B1C 平面AB1C,AC 平面AB1C,B1C∩AC=C,
所以AB⊥平面AB1C.
又因为AB 平面ABB1,所以平面AB1C⊥平面ABB1.
20.(本小题满分12分)如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,CD⊥PA,DB平分∠ADC,E为PC的中点,∠DAC=45°,AC=.
(1)求证:PA∥平面BDE;
(2)若PD=2,BD=2,求四棱锥E-ABCD的体积.
[解析] (1)设AC∩BD=F,连接EF.
∵PD⊥平面ABCD,CD 平面ABCD,∴PD⊥CD.
∵CD⊥PA,PA∩PD=P,∴CD⊥平面PAD.
∵AD 平面PAD,∴CD⊥AD.
∵∠DAC=45°,∴DA=DC.
∵DB平分∠ADC,∴F为AC的中点.
∵E为PC的中点,∴EF为△CPA的中位线,∴EF∥PA.
又EF 平面BDE,PA平面BDE,∴PA∥平面BDE.
(2)由(1)知DB⊥AC,将底面四边形ABCD的面积记为S,则S=S△ADC+S△ABC=××+××=2.
∵点E为线段PC的中点,
∴V四棱锥E-ABCD=S×PD=×2××2=.
21.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于D,E,又SA=AB,SB=BC.
(1)求证:BD⊥平面SAC;
(2)求二面角E-BD-C的大小.
[解析]
(1)证明:如图,
∵DE⊥SC,且E为SC的中点,又SB=BC,
∴BE⊥SC.
又DE∩BE=E,
根据直线与平面垂直的判定定理知SC⊥平面BDE,
∵BD 平面BDE,∴SC⊥BD.
又SA⊥平面ABC,BD 平面ABC,∴SA⊥BD.
又SA∩SC=S,∴BD⊥平面SAC.
(2)由(1)知∠EDC为二面角E-BD-C的平面角,又△SAC∽△DEC,∴∠EDC=∠ASC.
在Rt△SAB中,∠SAB=90°,
设SA=AB=1,则SB=.
由SA⊥BC,AB⊥BC,AB∩SA=A,
∴BC⊥平面SAB,SB 平面SAB,∴BC⊥SB.
在Rt△SBC中,SB=BC=,∠SBC=90°,则SC=2.
在Rt△SAC中,∠SAC=90°,SA=1,SC=2.
∴cos ∠ASC==,
∴∠ASC=60°,即二面角E-BD-C的大小为60°.
22.(本小题满分12分)已知梯形BFEC如图1所示,其中BF∥EC,EC=3,BF=2,四边形ABCD是边长为1的正方形,沿AD将四边形EDAF折起,使得平面EDAF⊥平面ABCD,得到如图2所示的几何体.
(1)求证:平面AEC⊥平面BDE;
(2)求点F到平面ABE的距离.
[解析] (1)∵平面EDAF⊥平面ABCD,DE 平面EDAF.
平面EDAF∩平面ABCD=AD,DE⊥AD,∴DE⊥平面ABCD,
∵AC 平面ABCD,∴DE⊥AC,
∵四边形ABCD是正方形,∴AC⊥BD
∵DE、BD 平面BDE,DE∩BD=D,∴AC⊥平面BDE,
∵AC 平面ACE,∴平面AEC⊥平面BDE.
(2)过点F作FG⊥AE于点G,
因为平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
AB 平面ABCD,AB⊥AD,
所以AB⊥平面ADEF,又FG 平面ADEF,所以AB⊥FG,
又AB∩AE=A,AB,AE 平面ABE,所以FG⊥平面ABE,
所以线段FG的长即为点F到平面ABE的距离,
AF=1,AE=,
S△AEF=×1×1=,S△ABE=×1×=,
由VB-AEF=VF-ABE,得S△ABE·FG=S△AEF·AB,即FG=,
所以FG=,
即点F到平面ABE的距离为.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
