黑龙江省海林市朝鲜族中学2022-2023学年高一下学期5月第二次月考数学试卷(含答案)
文档属性
| 名称 | 黑龙江省海林市朝鲜族中学2022-2023学年高一下学期5月第二次月考数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 11:35:29 | ||
图片预览



文档简介
黑龙江省海林市朝鲜族中学2022-2023学年度第二学期高一年级数学学科第二次考试(必修2)
一、单项选择题(每小题5分 共60分)
1.下面四个条件中,能确定一个平面的是( )
A.空间中的任意三点
B.空间中的两条直线
C.空间中的两条平行直线
D.空间中的一条直线和一个点
2.若,则z=( )
A.1–i B.1+i C.–i D.i
3.电影《长津湖之水门桥》于2022年2月1日上映.某新闻机构想了解市民对《长津湖之水门桥》的评价,决定从某市3个区按人口数用分层随机抽样的方法抽取一个样本.若3个区人口数之比为2:3:5,且人口最多的一个区抽出了100人,则这个样本的容量为( )
A.100 B.160 C.200 D.240
4.已知单位向量,,则下列说法正确的是( )
A. B. C. D.
5.已知平面四边形ABCD满足,则四边形ABCD是( )
A.正方形 B.平行四边形 C.菱形 D.梯形
6.在中,已知,,,则( )
A.1 B. C. D.3
7.正方体的六个面中相互平行的平面有 ( )
A.2对 B.3对 C.4对 D.1对.
8.已知平面α∥平面β,直线a α,b β,那么直线a与直线b一定( )
A.平行 B.异面 C.垂直 D.不相交
9.为保障食品安全,某监管部门对辖区内一家食品企业进行检查,现从其生产的某种产品中随机抽取100件作为样本,并以产品的一项关键质量指标值为检测依据,整理得到如下的样本频率分布直方图.若质量指标值在内的产品为一等品,则该企业生产的产品为一等品的概率约为( )
A.0.38 B.0.61
C.0.122 D.0.75
10.下列说法正确的是 ( )
A.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行
B.平行于同一个平面的两条直线平行
C.与两个相交平面的交线平行的直线,必平行于这两个平面
D.平面外两条平行直线中的一条与这个平面平行,则另一条也与这个平面平行
11.在正方体ABCD-A1B1C1D1中,异面直线AB1与BD的夹角为 ( )
A. B. C. D.
12.如图,在四面体DABC中,若AB=CB,AD=CD,E是AC的中点,则下列结论一定正
确的是 ( )
A.平面ABC⊥平面ABD
B.平面ABD⊥平面BDC
C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE
D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE
二、填空题(每小题5分,共20分)
13.平面向量a=(1,2),b=(3,4),则a+2b=___________.
14.若x1,x2,…,xa的平均数为a,则2x1+3,2x2+3,…,2xa+3的平均数为________.
15.已知△ABC的内角A,B,C的对边分别是a,b,c, 且b=3, a-c=2, A=.则△ABC的面积是________.
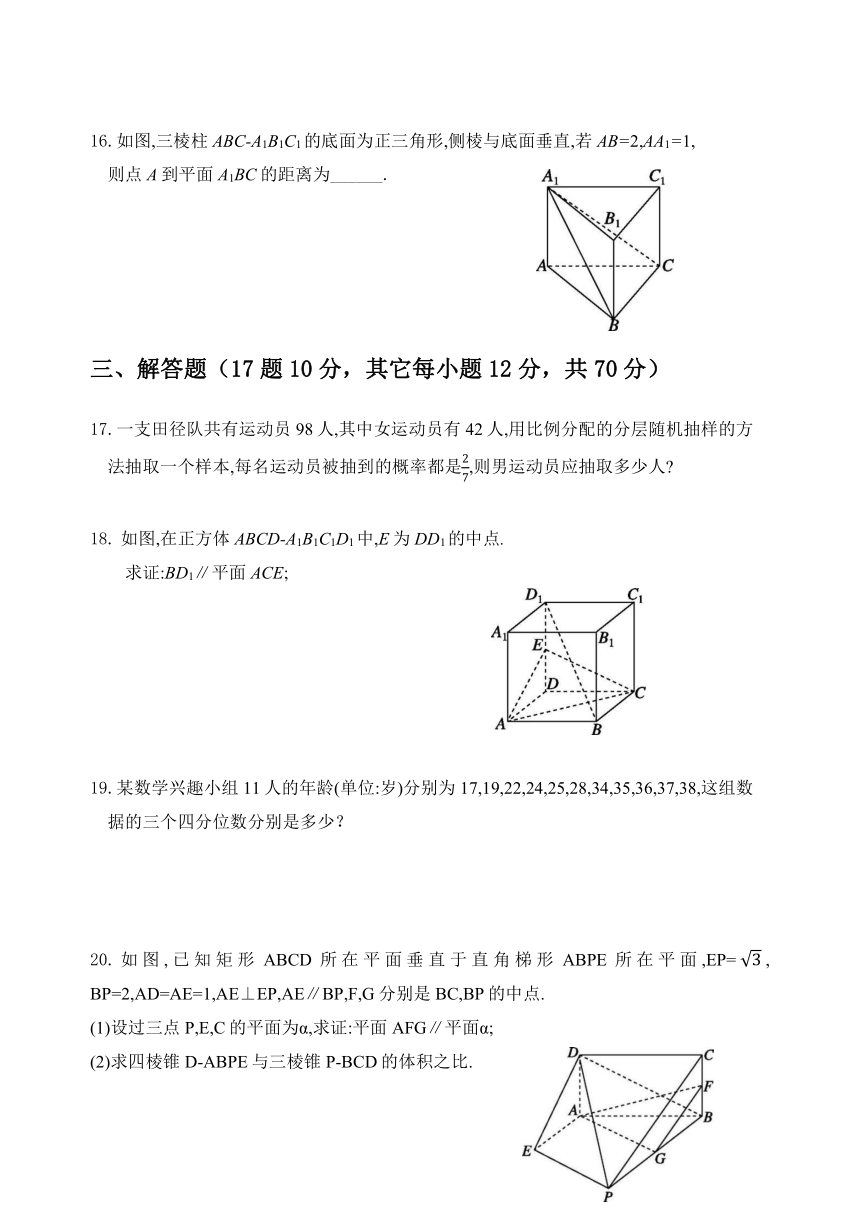
16.如图,三棱柱ABC-A1B1C1的底面为正三角形,侧棱与底面垂直,若AB=2,AA1=1,
则点A到平面A1BC的距离为______.
三、解答题(17题10分,其它每小题12分,共70分)
17.一支田径队共有运动员98人,其中女运动员有42人,用比例分配的分层随机抽样的方法抽取一个样本,每名运动员被抽到的概率都是,则男运动员应抽取多少人
18. 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.
求证:BD1∥平面ACE;
19.某数学兴趣小组11人的年龄(单位:岁)分别为17,19,22,24,25,28,34,35,36,37,38,这组数据的三个四分位数分别是多少?
20.如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,EP=, BP=2,AD=AE=1,AE⊥EP,AE∥BP,F,G分别是BC,BP的中点.
(1)设过三点P,E,C的平面为α,求证:平面AFG∥平面α;
(2)求四棱锥D-ABPE与三棱锥P-BCD的体积之比.
21.在△ABC中,内角A,B,C的对边分别为a,b,c,C=,AB边上的高为.
(1)若S△ABC=2,求△ABC的周长;
(2)求+的最大值.
22.如图,在三棱柱ABC-A1B1C1中,底面ABC是正三角形, AB=2,
侧棱A1A⊥平面ABC,D,E分别是AB,AA1的中点,且A1D⊥B1E.
(1)求证:B1E⊥平面A1CD;
(2)求点A1到平面B1CD的距离.
参考答案
1-12 CDCCB DBDBD BC
13.(7,10)
14.2a+3。
15..
16..
17.[解析] ∵田径队共有运动员98人,其中女运动员有42人,∴男运动员有56人,∵每名运动员被抽到的概率都是,∴男运动员应抽取56×=16(人)。
18. 证明:连接BD,设AC∩BD=F,连接EF,如图,则EF∥BD1,
又BD1 平面ACE,EF 平面ACE,所以BD1∥平面ACE.
19.[解析] 因为11×25%=2.75,11×50%=5.5,11×75%=8.25,所以这组数据的三个四分位数分别是第3,6,9个数据,即22,28,36.
20.解:(1)证明:∵G是BP的中点,∴PG=BP=1,
又∵AE=1,∴AE=PG.
又∵AE∥PG,AE⊥EP,∴四边形AEPG是矩形,∴AG∥EP.
∵AG 平面α,PE 平面α,∴AG∥平面α.
∵F,G分别是BC,BP的中点,∴FG是△BCP的中位线,∴FG∥PC.
∵FG 平面α,PC 平面α,∴FG∥平面α.∵AG∩FG=G,且AG,FG 平面AFG,
∴平面AFG∥平面α.
(2)过P作PH⊥AB,垂足为H,由题意得AD⊥平面ABPE,
∴V四棱锥D-ABPE=S梯形ABPE·AD=×××1=.
∵平面ABCD⊥平面ABPE,平面ABCD∩平面ABPE=AB,PH 平面ABPE,PH⊥AB,
∴PH⊥平面ABCD,即PH是三棱锥P-BCD的高.
∵AG=EP=,PG=AE=BG=1,
∴由勾股定理得AB===2.
CD=AB=2,sin∠ABG==,
∴PH=BP·sin∠ABG=2×=,∴V三棱锥P-BCD=×S△BCD×PH=××2×1×=,
∴四棱锥D-ABPE与三棱锥P-BCD的体积之比为=.
21.解:(1)∵S△ABC=ab·sin C=c·=2,∴c=4,∵C=,∴ab=8.
由余弦定理知,c2=a2+b2-2ab·cos C=(a+b)2-3ab,∴16=(a+b)2-3×8,
∴a+b=2,∴△ABC的周长为a+b+c=2+4.
(2)由(1)易知ab=2c,
由正弦定理知,==,
则+====
==
,
∵022.解:(1)证明:在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,CD 平面ABC,
所以AA1⊥CD.
在△ABC中,AC=BC,AD=BD,所以CD⊥AB.
又AA1∩AB=A,所以CD⊥平面AA1B1B.
因为B1E 平面AA1B1B,所以CD⊥B1E.
又B1E⊥A1D,A1D∩CD=D,
所以B1E⊥平面A1CD.
(2)在矩形AA1B1B中,因为B1E⊥A1D,
所以∠A1EB1=∠A1DA,
则tan∠A1EB1=tan∠A1DA,即=,即=,得AA1=2.
在Rt△BDC中,CD==.
由(1)知CD⊥平面AA1B1B,所以CD=即为点C到平面AA1B1B的距离.
在Rt△B1BD中,B1D==.
设点A1到平面B1CD的距离为h, 由=,
得·h=·CD,即×××h=××2×2×,解得h=,
所以点A1到平面B1CD的距离为.
一、单项选择题(每小题5分 共60分)
1.下面四个条件中,能确定一个平面的是( )
A.空间中的任意三点
B.空间中的两条直线
C.空间中的两条平行直线
D.空间中的一条直线和一个点
2.若,则z=( )
A.1–i B.1+i C.–i D.i
3.电影《长津湖之水门桥》于2022年2月1日上映.某新闻机构想了解市民对《长津湖之水门桥》的评价,决定从某市3个区按人口数用分层随机抽样的方法抽取一个样本.若3个区人口数之比为2:3:5,且人口最多的一个区抽出了100人,则这个样本的容量为( )
A.100 B.160 C.200 D.240
4.已知单位向量,,则下列说法正确的是( )
A. B. C. D.
5.已知平面四边形ABCD满足,则四边形ABCD是( )
A.正方形 B.平行四边形 C.菱形 D.梯形
6.在中,已知,,,则( )
A.1 B. C. D.3
7.正方体的六个面中相互平行的平面有 ( )
A.2对 B.3对 C.4对 D.1对.
8.已知平面α∥平面β,直线a α,b β,那么直线a与直线b一定( )
A.平行 B.异面 C.垂直 D.不相交
9.为保障食品安全,某监管部门对辖区内一家食品企业进行检查,现从其生产的某种产品中随机抽取100件作为样本,并以产品的一项关键质量指标值为检测依据,整理得到如下的样本频率分布直方图.若质量指标值在内的产品为一等品,则该企业生产的产品为一等品的概率约为( )
A.0.38 B.0.61
C.0.122 D.0.75
10.下列说法正确的是 ( )
A.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行
B.平行于同一个平面的两条直线平行
C.与两个相交平面的交线平行的直线,必平行于这两个平面
D.平面外两条平行直线中的一条与这个平面平行,则另一条也与这个平面平行
11.在正方体ABCD-A1B1C1D1中,异面直线AB1与BD的夹角为 ( )
A. B. C. D.
12.如图,在四面体DABC中,若AB=CB,AD=CD,E是AC的中点,则下列结论一定正
确的是 ( )
A.平面ABC⊥平面ABD
B.平面ABD⊥平面BDC
C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE
D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE
二、填空题(每小题5分,共20分)
13.平面向量a=(1,2),b=(3,4),则a+2b=___________.
14.若x1,x2,…,xa的平均数为a,则2x1+3,2x2+3,…,2xa+3的平均数为________.
15.已知△ABC的内角A,B,C的对边分别是a,b,c, 且b=3, a-c=2, A=.则△ABC的面积是________.
16.如图,三棱柱ABC-A1B1C1的底面为正三角形,侧棱与底面垂直,若AB=2,AA1=1,
则点A到平面A1BC的距离为______.
三、解答题(17题10分,其它每小题12分,共70分)
17.一支田径队共有运动员98人,其中女运动员有42人,用比例分配的分层随机抽样的方法抽取一个样本,每名运动员被抽到的概率都是,则男运动员应抽取多少人
18. 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.
求证:BD1∥平面ACE;
19.某数学兴趣小组11人的年龄(单位:岁)分别为17,19,22,24,25,28,34,35,36,37,38,这组数据的三个四分位数分别是多少?
20.如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,EP=, BP=2,AD=AE=1,AE⊥EP,AE∥BP,F,G分别是BC,BP的中点.
(1)设过三点P,E,C的平面为α,求证:平面AFG∥平面α;
(2)求四棱锥D-ABPE与三棱锥P-BCD的体积之比.
21.在△ABC中,内角A,B,C的对边分别为a,b,c,C=,AB边上的高为.
(1)若S△ABC=2,求△ABC的周长;
(2)求+的最大值.
22.如图,在三棱柱ABC-A1B1C1中,底面ABC是正三角形, AB=2,
侧棱A1A⊥平面ABC,D,E分别是AB,AA1的中点,且A1D⊥B1E.
(1)求证:B1E⊥平面A1CD;
(2)求点A1到平面B1CD的距离.
参考答案
1-12 CDCCB DBDBD BC
13.(7,10)
14.2a+3。
15..
16..
17.[解析] ∵田径队共有运动员98人,其中女运动员有42人,∴男运动员有56人,∵每名运动员被抽到的概率都是,∴男运动员应抽取56×=16(人)。
18. 证明:连接BD,设AC∩BD=F,连接EF,如图,则EF∥BD1,
又BD1 平面ACE,EF 平面ACE,所以BD1∥平面ACE.
19.[解析] 因为11×25%=2.75,11×50%=5.5,11×75%=8.25,所以这组数据的三个四分位数分别是第3,6,9个数据,即22,28,36.
20.解:(1)证明:∵G是BP的中点,∴PG=BP=1,
又∵AE=1,∴AE=PG.
又∵AE∥PG,AE⊥EP,∴四边形AEPG是矩形,∴AG∥EP.
∵AG 平面α,PE 平面α,∴AG∥平面α.
∵F,G分别是BC,BP的中点,∴FG是△BCP的中位线,∴FG∥PC.
∵FG 平面α,PC 平面α,∴FG∥平面α.∵AG∩FG=G,且AG,FG 平面AFG,
∴平面AFG∥平面α.
(2)过P作PH⊥AB,垂足为H,由题意得AD⊥平面ABPE,
∴V四棱锥D-ABPE=S梯形ABPE·AD=×××1=.
∵平面ABCD⊥平面ABPE,平面ABCD∩平面ABPE=AB,PH 平面ABPE,PH⊥AB,
∴PH⊥平面ABCD,即PH是三棱锥P-BCD的高.
∵AG=EP=,PG=AE=BG=1,
∴由勾股定理得AB===2.
CD=AB=2,sin∠ABG==,
∴PH=BP·sin∠ABG=2×=,∴V三棱锥P-BCD=×S△BCD×PH=××2×1×=,
∴四棱锥D-ABPE与三棱锥P-BCD的体积之比为=.
21.解:(1)∵S△ABC=ab·sin C=c·=2,∴c=4,∵C=,∴ab=8.
由余弦定理知,c2=a2+b2-2ab·cos C=(a+b)2-3ab,∴16=(a+b)2-3×8,
∴a+b=2,∴△ABC的周长为a+b+c=2+4.
(2)由(1)易知ab=2c,
由正弦定理知,==,
则+====
==
,
∵0
所以AA1⊥CD.
在△ABC中,AC=BC,AD=BD,所以CD⊥AB.
又AA1∩AB=A,所以CD⊥平面AA1B1B.
因为B1E 平面AA1B1B,所以CD⊥B1E.
又B1E⊥A1D,A1D∩CD=D,
所以B1E⊥平面A1CD.
(2)在矩形AA1B1B中,因为B1E⊥A1D,
所以∠A1EB1=∠A1DA,
则tan∠A1EB1=tan∠A1DA,即=,即=,得AA1=2.
在Rt△BDC中,CD==.
由(1)知CD⊥平面AA1B1B,所以CD=即为点C到平面AA1B1B的距离.
在Rt△B1BD中,B1D==.
设点A1到平面B1CD的距离为h, 由=,
得·h=·CD,即×××h=××2×2×,解得h=,
所以点A1到平面B1CD的距离为.
同课章节目录
