四川成都2023年中考数学模拟考场仿真演练卷(含解析)
文档属性
| 名称 | 四川成都2023年中考数学模拟考场仿真演练卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 17:39:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
绝密★启用前
2023年成都中考数学模拟考场仿真演练卷
数 学
本卷满分120分,考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.有理数2022的相反数是( )
A.2022 B.-2022 C. D.
2.将如图所示的无盖正方体沿边AB,BC,DE,EF剪开后展开,则下列展开图的示意图正确的是( )
A.B.C. D.
3.2022北京新闻中心于2月17日举行的新闻发布会上发布:“带动三亿人参与冰雪运动”庄严承诺已经实现.这是北京冬奥会最重要的遗产成果.数据300 000 000用科学记数法表示为( )
A.3×107 B.30×107 C.3×108 D.0.3×109
4.若点P(a-1,a+2)在x轴上,则a的值为( )
A.-1 B.1 C.-2 D.2
5.下列运算正确的是( )
A. B. C. D.
6.如图,平行四边形中,、是对角线上的两点,,则添加①;②;③;④中任意一个条件能够使,共有几种方法( )
A.1 B.2 C.3 D.4
7.在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
8.已知是二元一次方程组的解,则的算术平方根为( )
A.± B. C.±2 D.2
9.唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:今携一壶酒,游春郊外走.逢朋加一倍,入店饮斗九.相逢三处店,饮尽壶中酒.试问能算士:如何知原有.大意是:李白在郊外春游时,遇见一个朋友,先将壶里的酒增加一倍,再喝掉其中的19升酒.按照这样的约定,在第3次遇到朋友后正好喝光了壶中的酒,设壶中原有酒为x升,则可列出方程为( )
A. B.
C. D.
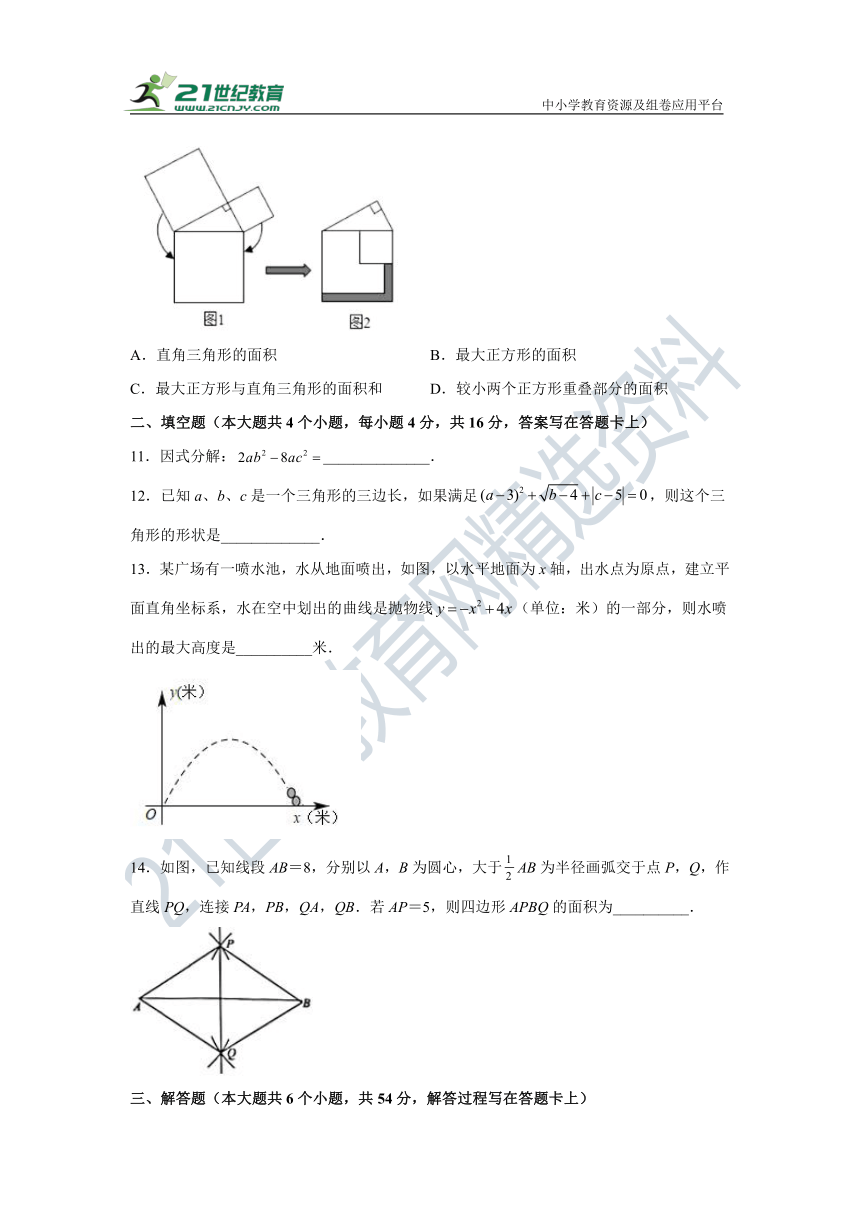
10.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2.则图2中阴影部分面积等于( )
A.直角三角形的面积 B.最大正方形的面积
C.最大正方形与直角三角形的面积和 D.较小两个正方形重叠部分的面积
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.因式分解:______________.
12.已知a、b、c是一个三角形的三边长,如果满足,则这个三角形的形状是_____________.
13.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是__________米.
14.如图,已知线段AB=8,分别以A,B为圆心,大于AB为半径画弧交于点P,Q,作直线PQ,连接PA,PB,QA,QB.若AP=5,则四边形APBQ的面积为__________.
三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(12分)(1)计算:
(2)解方程组:.
16.(6分)先化简,再求值: ,其中m=+3.
17.(8分)2021年7月24日,中共中央办公厅,国务院办公厅发布《关于进一步减轻义务教育阶段学生作业负担和课外培训负担的意见》,该意见要求初中书面作业平均完成时间不超过90分钟.为了解实施情况,天府新区某调查组随机调查了某初中学校部分同学最近一周完成家庭作业的时间,得到他们平均每天完成家庭作业时长(单位:分)的一组数据,将所得数据分为四组(:,:,:,:),并绘制成如图所示两幅不完整的统计图.
根据如图所示信息,解答下列问题:
(1)调查组一共抽样调查了____________名同学;在扇形统计图中,表示组的扇形圆心角的度数为____________;
(2)将条形统计图补充完整;
(3)组的4名学生是3名男生.和1名女生,若从他们中任选2人了解最近一周平均每天完成家庭作业时间较长的原因,试求恰好选中1名男生和1名女生的概率.
18.(8分)如图1是2022年北京冬奥会首钢滑雪大跳台,曲线的设计灵感来自敦煌“飞天”飘带,又名“雪飞天”,它是世界上首例永久性保留和使用的滑雪大跳台场馆.如图2,为测量“雪飞天”的高度,测得大跳台跨度AB为140m,出发区CD为20m,且,AD为大跳台钢支架,在点A处测得点D的仰角∠DAB=75°,在点C处测得点B的俯角∠ECB=30°.(测角仪的高度忽略不计)
(1)求大跳台出发区CD距离地面AB的高度.(结果精确到1m;参考数据:,,,)
(2)据了解,“雪飞天”需要造雪,分别用雪枪和雪炮来满足对于雪量和雪质的不同要求,雪炮出雪量大,适合室外滑雪场快速铺雪,雪枪造雪分布比较平均,相对造雪量比较小.若每台雪枪每小时出雪量比雪炮少,且一台雪枪出雪所用的时间与一台雪炮出雪所用的时间相等.求每台雪枪和雪炮每小时的出雪量.
19.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数(a≠0)的图象交于A、B两点,与x轴交于点C,过点A作ADy轴于点D,点O是线段CD的中点,AC=,sin∠ACD=,点B的坐标为(m,-2)
(1)求反比例函数和一次函数的函数表达式;
(2)求△ABD的面积.
(3)观察图象,直接写出关于的不等式>的解集.
20.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作MN⊥AC,垂足为M,交AB的延长线于点N,过点B作BG⊥MN,垂足为G,连接CM.
(1)求证:直线MN是⊙O的切线;
(2)求证:BD2=AC BG;
(3)若BN=OB,⊙O的半径为1,求tan∠ANC的值.
B卷
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
1.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△BOC的面积为_________.
2.若a、b是方程的两根,则_______________.
3.如图所示,直线与x轴、y轴分别交于点M,N,的半径为1,将以每秒1个单位的速度向右作平移运动,当移动_________秒时,直线恰好与相切.
4.如图,矩形中,,,F为边上一点,连接,将沿折叠,得到,G为上一点,将沿折叠,使点的对应点落在上,当点恰好在矩形的对角线上时,线段的长为________.
5.已知两个正数a,b,可按规则扩充为一个新数c在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作,(1)若,按上述规则操作三次,扩充所得的数是_________;(2)若,经过6次操作后扩充所得的数为(m,n为正整数),则的值为________.
二、解答题(本大题共3个小题,共30分,答过程写在答题卡上)
6.(8分)某商店销售A、B、C三种型号的饮料.随着夏季来临,天气逐渐炎热,该商店决定从今年5月1日起将A饮料每瓶的价格上调20%,将B饮料每瓶的价格下调10%,C饮料价格不变,是每瓶7元,已知调价前A、B、C三种饮料各买一瓶共花费18元,调价后买A饮料2瓶、B饮料5瓶共花费39元.
(1)问A、B两种饮料调价前的单价;
(2)今年6月份,温州某单位花费3367元在该商店购买A、B、C三种饮料共n瓶,其中购得B饮料的瓶数是A饮料的2倍,求n的最大值.
7.(10分)某学习小组开展了图形旋转的探究活动:将一个矩形绕点A顺时针旋转,得到矩形,连结.
(1)如图1,当时,点恰好在延长线上.若,求的长.
(2)如图2,连结,过点作交于点M.观察思考线段与数量关系并说明理由.
(3)在(2)的条件下,射线交于点N(如图3),若,旋转角等于多少度时是等边三角形,请写出的值,并说明是等边三角形的理由.
8.(12分)已知抛物线交x轴交于和点,交y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,点D是直线BC上一点,过点D作轴,交抛物线于点E(点E在点D的上方),再过点E作轴,交直线BC于点F.当的面积取最大值时,求点E的坐标;
(3)如图2,点M为抛物线对称轴l上的一点,点N为抛物线上的一点,当直线BC垂直平分MN时,求出点N的坐标.
全解全析
1 2 3 4 5 6 7 8 9 10
B B C C C C B B D D
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.【答案】B
【解析】有理数2022的相反数是-2022;故选B
2.【答案】B
【解析】如图所示的无盖正方体沿边AB,BC,DE,EF剪开后展开图形为
故选:B.
3.【答案】C
【解析】用科学记数法表示300 000 000=3×108;故选:C.
4.【答案】C
【解析】∵点P(a-1,a+2)在x轴上,∴a+2=0,解得a=﹣2,故选:C.
5.【答案】C
【解析】A、x-2x=-x,故此选项不符合题意;
B、(x-1)2=x2-2x+1,故此选项不符合题意;
C、,故此选项符合题意;
D、x2+x2=2x2,故此选项不符合题意; 故选:C.
6.【答案】C
【解析】∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴∠ABE=∠CDF
当添加时,由AB=CD,∠ABE=∠CDF,BE=DF用SAS可证;
当添加时,可知∠AEF=∠CFE,则∠AEB=∠CFD,又∵AB=CD,∠ABE=∠CDF,用AAS可证;
当添加时,由AB=CD,∠ABE=∠CDF,和不能证明;
当添加时,由AB=CD,∠ABE=∠CDF,可证;
共有3种方法,故选C.
7.在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
【答案】B
【解析】∵6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,
∴众数要变,故C不符合题意;平均数与每个数有关,因此平均数也要变,故A不符合题意;方差与每个数据有关,数据变了方差也要变化,故D不符合题意;中位数是82.5,不会变化,故B符合题意;
故答案为:B.
8.【答案】B
【解析】把代入二元一次方程组得:,解得:,
则==2,∴2的算术平方根为,故选:B.
9.【答案】D
【解析】设壶中原有酒为x升,根据题意得,;故选D
10.【答案】D
【解析】如图,设直角三角形的较短直角边为a,较长直角边为b,斜边为c,
由勾股定理可得,,
阴影部分面积,
较小两个正方形重叠部分的面积,
∴阴影部分面积=较小两个正方形重叠部分的面积.故选:D.
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.【答案】
【解析】
,
故答案为:.
12.【答案】直角三角形
【解析】由题意得: ,
解得:,
∵,
∴三角形为直角三角形.
故答案为直角三角形.
13.【答案】4
【解析】∵,
∴顶点坐标是(2,4),
∴最大高度是4米.故答案为:4.
14.【答案】
【解析】由题意知,
是的垂直平分线,如下图:
,
,
,
,
四边形APBQ为菱形,
,
,
,
,故答案为:.
三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(12分)(1)【答案】
【解析】
.
(2)【答案】
【解析】
①×2+②,得11=33
解得=3
把=3代入①,解得=3
∴原方程组的解是.
16.(6分)【答案】m-3,
【解析】原式=
=m-3,
当m=+3时,
原式= m=+3-3=.
17.(8分)【答案】(1)50,108°;(2)见解析;(3)
【解析】(1)调查组一共抽样调查了名同学;
(2)C组的人数为(人),补全统计图如图,
(3)设男生分别为A1,A2,A3,女生为B,列表如下,
A1 A2 A3 B
A1 A1A2 A1A3 A1B
A2 A2A1 A2A3 A2B
A3 A3A1 A3A2 A3B
B B A1 B A2 B A3
恰好选中1名男生和1名女生的概率为
18.(8分)【答案】(1);(2)每台雪炮每小时的出雪量为,每台雪枪每小时的出雪量为.
【解析】(1)如解图,过点D,C分别作AB的垂线,垂足分别为F,G,则四边形CDFG是矩形.
∴FG=CD=20m,CG=DF,.
∴∠CBG=∠ECB=30°.
在Rt△BCG中,,
∴.
在Rt△ADF中,∠DAF=75°,,
∴.
又∵AF+FG+BG=AB,AB=140m,
∴.
解得DF≈60.
答:大跳台出发区CD距离地面AB的高度约为60m.
(2)设每台雪炮每小时的出雪量为,则每台雪枪每小时的出雪量为.
根据题意,得,解得x=60.
经检验,x=60是原方程的解,且符合题意.
∴60-40=20().
答:每台雪炮每小时的出雪量为,每台雪枪每小时的出雪量为.
19.(10分)【答案】(1),;(2)6;(3)或
【解析】(1)解:∵轴于点D,
∴轴于点D,
,,
∴,即,
解得.
在Rt△ACD中,
∵,
∴.
∵点O是线段CD的中点,
∴,
∴,
∴反比例函数表达式为.
∵点B的坐标为
∴.
∴设一次函数表达式为,
则解得
∴一次函数解析式为.
(2)由(1),得.
(3)观察函数图象知,当时,
或.
20.(10分)【答案】(1)见解析;(2)见解析;(3)
【解析】(1)
证明:如图1,
连接AD,OD,
∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD,BD=CD,
∵OA=OD,
∴∠ODA=∠BAD,
∴∠ODA=∠CAD,
∵NM⊥AC,
∴∠AMN=90°,
∴∠DAC+∠ADM=90°,
∴∠ODA+∠ADM=90°,即∠ODM=90°,
∴OD⊥MN,
∴直线MN是⊙O的切线;
(2)证明:由(1)知,∠ADC=90°,BD=CD,
∴∠ADC=∠DMC=90°,
∵∠ACD=∠DCM,
∴△CMD∽△CDA,
∴,
∴CD2=AC CM,
∴BD2=AC CM,
在△BGD和△CMD中,,
∴△BGD≌△CMD(AAS),
∴BG=CM,
∴BD2=AC BG;
(3)解:如图2,
连接OD,OC,由(1)知∠ODN=90°,
∵OD=OB=BN=1,
∴cos∠DON=,
∴∠DON=60°,
∵OB=OD,
∴∠OBD=60°,
∵AB=AC,
∴△ABC是等边三角形,
∵OA=OB,
∴CO⊥AB,OC=AC sin60°=,
∴tan∠ANC=.
B卷
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
1.【答案】3
【解析】点是斜边的中点,且点的坐标为,
,即,
将点代入双曲线得:,
则双曲线的解析式为,
又,,且点在上,
,点的横坐标与点的横坐标相同,即为,
当时,,即,
,
则的面积为,故答案为:3.
2.【答案】2021
【解析】∵a、b是方程x2 +x- 2022 = 0的两根,
∴ a2+a- 2022 = 0, a+b= -1,
∴a2+a= 2022,
∴a2+ 2a+b=a2 +a+a+b= 2022-1=2021
故答案为:2021
3.【答案】或
【解析】作EF平行于MN,且与⊙O切,交x轴于点E,交y轴于点F,如图所示.
设直线EF的解析式为y=x+b,即x-y+b=0,
∵EF与⊙O相切,且⊙O的半径为1,
∴,
解得:b=或b=,
∴直线EF的解析式为或,
∴点E的坐标为(,0)或(,0).
令y=x2中y=0,则x=2,
∴点M(2,0).
∵根据运动的相对性,且⊙O以每秒1个单位的速度向右作平移运动,
∴移动的时间为秒或秒.
故答案为:或.
4.【答案】或
【解析】如图,①当点在对角线上时,点和点重合,如解图 1 所示.
,,
四边形是矩形,,
,
折叠,
,
②当点在对角线上时,连接,过点作于点, 过点 作 于点 , 如解 图 2 所示.
同理可得.
在 Rt 中,
.
.
.
综上所述, 线段 的长为 或 .故答案为:或
5.【答案】 255 21
【解析】(1)第一次,;第二次,;第三次,;
(2)第一次,;
第二次,;
第三次;
第四次,;
第五次,;
第六次,,所以.
故答案为(1)255;(2)21.
二、解答题(本大题共3个小题,共30分,答过程写在答题卡上)
6.(8分)【答案】(1)A种饮料调价前的单价为5元/瓶,B种饮料调价前的单价为6元/瓶
(2)n的最大值为601
【解析】(1)解:设A、B饮料在调价前每瓶各x元、y元,
根据题意得: 解得:
答:A种饮料调价前的单价为5元/瓶,B种饮料调价前的单价为6元/瓶;
(2)解:设购进A饮料m瓶,则购进B饮料2m瓶,购进C饮料(n-3m)瓶
根据题意得: 解得:n=481+0.6m
购买A、B两种饮料的钱数要少于3367元
解得:
又m、n均为整数
当m=200时,n取得最大值,最大值为601
答:n的最大值为601.
7.(10分)【答案】(1)1+;(2)M=DM,理由见解析;(3)=60°,理由见解析.
【解析】(1)解:∵四边形ABCD是矩形,
∴CD=AB,BC=DA,∠BAD=90°,
∵将矩形ABCD绕点A顺时针旋转90°得到矩形,
∴∠AD=∠BAD=90°,=CD=AB=2,
∴AB与A重合,即点A、B、在同一条直线上,
设BC=DA=A=x,则B=x﹣2,
∵∠=∠BAD=90°,∠B=∠ABD,
∴△B∽△∠ABD,
∴,
∴,
解得x1=1+,x2=1-(不符合题意,舍去),
∴BC=1+.
(2)解:M=DM,理由如下:
如图4,连结D,
∵A=AD,
∴∠AD=∠AD,
∵=AB,∠A=∠BAD=90°,A=DA,
∴△A≌△BAD(SAS),
∴∠A=∠ADB,
∵MA,
∴∠AM=∠A,
∴∠AM=∠ADB,
∴∠AD﹣∠AM=∠AD﹣∠ADB,
∴∠MD=∠MD,
∴M=DM.
(3)解:=60°,理由如下:
如图5,连结AM,
∵A=AD,M=DM,AM=AM,
∴△AM≌△ADM(SSS),
∴∠AM=∠ADM,∠MA=∠MAD=∠DA==30°,
∵∠AM=∠NA,
∴∠NA=∠ADM=30°,
∴∠NA+∠MA=∠ADM+∠MAD=60°,
∵∠NAM=∠NA+∠MA,∠NMA=∠ADM+∠MAD,
∴∠NAM=∠NMA,
∴MN=AN,
∴△AMN是等腰三角形,
∵∠NAM=∠NA+∠MA=60°,
∴△AMN是等边三角形.
8.(12分)【答案】(1);(2);(3)或
【解析】(1)解:∵抛物线交x轴交于和点,
设,
∵当x=0时,y=3,
∴,解得a=-1,
∴,即.
(2)解:设直线BC的解析式为:y=kx+b(k≠0),
∵B(3,0),C(0,3),
则 ,解得,
∴y=-x+3,
设D(m,-m+3),
∴E(m,-m2+2m+3),
∵DE= yE-yD=-m2+2m+3-(-m+3)=-m2+3m,
由(1)得,OB=OC=3,
∴△BOC为等腰直角三角形,
∵DE∥OC,EF∥OB,
∴△DEF为等腰直角三角形,
∴ ,
∵点E在点D的上方,
∴0∵ ,
∴当 时,DE的最大值为 ,
∴的最大值为 ;
(3)解:如图,与直线相交与,连接ND,
∵BC是MN的对称轴,
∴ND=MD,
由(2)知△BOC是等腰直角三角形,
∴∠BDH=∠CBO=45°,
∴∠CDM=∠BDH=45°,
∴△MDN是等腰直角三角形,
∴抛物线的对称轴为 ,
设M(1,p),D(1,-1+3),即(1,2),
∵ND=MD=p-2,
当M点在D点上方时,
∴xN=1-(p-2)=-p+3,
∴N(-p+3, 2)
∵N点在抛物线上,
∴ ,
解得或(舍去),
∴N点坐标 ;
当M点在D点下方时,
同理得出为等腰直角三角形,
∴ ,
设的坐标为 ,
∴ ,
∴xN’=(2-q)+1=3-q,
∴N’(3-q, 2),
∵N’点在抛物线上,
∴ ,解得(舍去)或,
∴,
综上,N点坐标为或.
绝密★启用前
2023年成都中考数学模拟考场仿真演练卷
数 学
本卷满分120分,考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.有理数2022的相反数是( )
A.2022 B.-2022 C. D.
2.将如图所示的无盖正方体沿边AB,BC,DE,EF剪开后展开,则下列展开图的示意图正确的是( )
A.B.C. D.
3.2022北京新闻中心于2月17日举行的新闻发布会上发布:“带动三亿人参与冰雪运动”庄严承诺已经实现.这是北京冬奥会最重要的遗产成果.数据300 000 000用科学记数法表示为( )
A.3×107 B.30×107 C.3×108 D.0.3×109
4.若点P(a-1,a+2)在x轴上,则a的值为( )
A.-1 B.1 C.-2 D.2
5.下列运算正确的是( )
A. B. C. D.
6.如图,平行四边形中,、是对角线上的两点,,则添加①;②;③;④中任意一个条件能够使,共有几种方法( )
A.1 B.2 C.3 D.4
7.在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
8.已知是二元一次方程组的解,则的算术平方根为( )
A.± B. C.±2 D.2
9.唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:今携一壶酒,游春郊外走.逢朋加一倍,入店饮斗九.相逢三处店,饮尽壶中酒.试问能算士:如何知原有.大意是:李白在郊外春游时,遇见一个朋友,先将壶里的酒增加一倍,再喝掉其中的19升酒.按照这样的约定,在第3次遇到朋友后正好喝光了壶中的酒,设壶中原有酒为x升,则可列出方程为( )
A. B.
C. D.
10.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2.则图2中阴影部分面积等于( )
A.直角三角形的面积 B.最大正方形的面积
C.最大正方形与直角三角形的面积和 D.较小两个正方形重叠部分的面积
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.因式分解:______________.
12.已知a、b、c是一个三角形的三边长,如果满足,则这个三角形的形状是_____________.
13.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是__________米.
14.如图,已知线段AB=8,分别以A,B为圆心,大于AB为半径画弧交于点P,Q,作直线PQ,连接PA,PB,QA,QB.若AP=5,则四边形APBQ的面积为__________.
三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(12分)(1)计算:
(2)解方程组:.
16.(6分)先化简,再求值: ,其中m=+3.
17.(8分)2021年7月24日,中共中央办公厅,国务院办公厅发布《关于进一步减轻义务教育阶段学生作业负担和课外培训负担的意见》,该意见要求初中书面作业平均完成时间不超过90分钟.为了解实施情况,天府新区某调查组随机调查了某初中学校部分同学最近一周完成家庭作业的时间,得到他们平均每天完成家庭作业时长(单位:分)的一组数据,将所得数据分为四组(:,:,:,:),并绘制成如图所示两幅不完整的统计图.
根据如图所示信息,解答下列问题:
(1)调查组一共抽样调查了____________名同学;在扇形统计图中,表示组的扇形圆心角的度数为____________;
(2)将条形统计图补充完整;
(3)组的4名学生是3名男生.和1名女生,若从他们中任选2人了解最近一周平均每天完成家庭作业时间较长的原因,试求恰好选中1名男生和1名女生的概率.
18.(8分)如图1是2022年北京冬奥会首钢滑雪大跳台,曲线的设计灵感来自敦煌“飞天”飘带,又名“雪飞天”,它是世界上首例永久性保留和使用的滑雪大跳台场馆.如图2,为测量“雪飞天”的高度,测得大跳台跨度AB为140m,出发区CD为20m,且,AD为大跳台钢支架,在点A处测得点D的仰角∠DAB=75°,在点C处测得点B的俯角∠ECB=30°.(测角仪的高度忽略不计)
(1)求大跳台出发区CD距离地面AB的高度.(结果精确到1m;参考数据:,,,)
(2)据了解,“雪飞天”需要造雪,分别用雪枪和雪炮来满足对于雪量和雪质的不同要求,雪炮出雪量大,适合室外滑雪场快速铺雪,雪枪造雪分布比较平均,相对造雪量比较小.若每台雪枪每小时出雪量比雪炮少,且一台雪枪出雪所用的时间与一台雪炮出雪所用的时间相等.求每台雪枪和雪炮每小时的出雪量.
19.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数(a≠0)的图象交于A、B两点,与x轴交于点C,过点A作ADy轴于点D,点O是线段CD的中点,AC=,sin∠ACD=,点B的坐标为(m,-2)
(1)求反比例函数和一次函数的函数表达式;
(2)求△ABD的面积.
(3)观察图象,直接写出关于的不等式>的解集.
20.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作MN⊥AC,垂足为M,交AB的延长线于点N,过点B作BG⊥MN,垂足为G,连接CM.
(1)求证:直线MN是⊙O的切线;
(2)求证:BD2=AC BG;
(3)若BN=OB,⊙O的半径为1,求tan∠ANC的值.
B卷
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
1.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△BOC的面积为_________.
2.若a、b是方程的两根,则_______________.
3.如图所示,直线与x轴、y轴分别交于点M,N,的半径为1,将以每秒1个单位的速度向右作平移运动,当移动_________秒时,直线恰好与相切.
4.如图,矩形中,,,F为边上一点,连接,将沿折叠,得到,G为上一点,将沿折叠,使点的对应点落在上,当点恰好在矩形的对角线上时,线段的长为________.
5.已知两个正数a,b,可按规则扩充为一个新数c在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作,(1)若,按上述规则操作三次,扩充所得的数是_________;(2)若,经过6次操作后扩充所得的数为(m,n为正整数),则的值为________.
二、解答题(本大题共3个小题,共30分,答过程写在答题卡上)
6.(8分)某商店销售A、B、C三种型号的饮料.随着夏季来临,天气逐渐炎热,该商店决定从今年5月1日起将A饮料每瓶的价格上调20%,将B饮料每瓶的价格下调10%,C饮料价格不变,是每瓶7元,已知调价前A、B、C三种饮料各买一瓶共花费18元,调价后买A饮料2瓶、B饮料5瓶共花费39元.
(1)问A、B两种饮料调价前的单价;
(2)今年6月份,温州某单位花费3367元在该商店购买A、B、C三种饮料共n瓶,其中购得B饮料的瓶数是A饮料的2倍,求n的最大值.
7.(10分)某学习小组开展了图形旋转的探究活动:将一个矩形绕点A顺时针旋转,得到矩形,连结.
(1)如图1,当时,点恰好在延长线上.若,求的长.
(2)如图2,连结,过点作交于点M.观察思考线段与数量关系并说明理由.
(3)在(2)的条件下,射线交于点N(如图3),若,旋转角等于多少度时是等边三角形,请写出的值,并说明是等边三角形的理由.
8.(12分)已知抛物线交x轴交于和点,交y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,点D是直线BC上一点,过点D作轴,交抛物线于点E(点E在点D的上方),再过点E作轴,交直线BC于点F.当的面积取最大值时,求点E的坐标;
(3)如图2,点M为抛物线对称轴l上的一点,点N为抛物线上的一点,当直线BC垂直平分MN时,求出点N的坐标.
全解全析
1 2 3 4 5 6 7 8 9 10
B B C C C C B B D D
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.【答案】B
【解析】有理数2022的相反数是-2022;故选B
2.【答案】B
【解析】如图所示的无盖正方体沿边AB,BC,DE,EF剪开后展开图形为
故选:B.
3.【答案】C
【解析】用科学记数法表示300 000 000=3×108;故选:C.
4.【答案】C
【解析】∵点P(a-1,a+2)在x轴上,∴a+2=0,解得a=﹣2,故选:C.
5.【答案】C
【解析】A、x-2x=-x,故此选项不符合题意;
B、(x-1)2=x2-2x+1,故此选项不符合题意;
C、,故此选项符合题意;
D、x2+x2=2x2,故此选项不符合题意; 故选:C.
6.【答案】C
【解析】∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴∠ABE=∠CDF
当添加时,由AB=CD,∠ABE=∠CDF,BE=DF用SAS可证;
当添加时,可知∠AEF=∠CFE,则∠AEB=∠CFD,又∵AB=CD,∠ABE=∠CDF,用AAS可证;
当添加时,由AB=CD,∠ABE=∠CDF,和不能证明;
当添加时,由AB=CD,∠ABE=∠CDF,可证;
共有3种方法,故选C.
7.在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
【答案】B
【解析】∵6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,
∴众数要变,故C不符合题意;平均数与每个数有关,因此平均数也要变,故A不符合题意;方差与每个数据有关,数据变了方差也要变化,故D不符合题意;中位数是82.5,不会变化,故B符合题意;
故答案为:B.
8.【答案】B
【解析】把代入二元一次方程组得:,解得:,
则==2,∴2的算术平方根为,故选:B.
9.【答案】D
【解析】设壶中原有酒为x升,根据题意得,;故选D
10.【答案】D
【解析】如图,设直角三角形的较短直角边为a,较长直角边为b,斜边为c,
由勾股定理可得,,
阴影部分面积,
较小两个正方形重叠部分的面积,
∴阴影部分面积=较小两个正方形重叠部分的面积.故选:D.
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.【答案】
【解析】
,
故答案为:.
12.【答案】直角三角形
【解析】由题意得: ,
解得:,
∵,
∴三角形为直角三角形.
故答案为直角三角形.
13.【答案】4
【解析】∵,
∴顶点坐标是(2,4),
∴最大高度是4米.故答案为:4.
14.【答案】
【解析】由题意知,
是的垂直平分线,如下图:
,
,
,
,
四边形APBQ为菱形,
,
,
,
,故答案为:.
三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(12分)(1)【答案】
【解析】
.
(2)【答案】
【解析】
①×2+②,得11=33
解得=3
把=3代入①,解得=3
∴原方程组的解是.
16.(6分)【答案】m-3,
【解析】原式=
=m-3,
当m=+3时,
原式= m=+3-3=.
17.(8分)【答案】(1)50,108°;(2)见解析;(3)
【解析】(1)调查组一共抽样调查了名同学;
(2)C组的人数为(人),补全统计图如图,
(3)设男生分别为A1,A2,A3,女生为B,列表如下,
A1 A2 A3 B
A1 A1A2 A1A3 A1B
A2 A2A1 A2A3 A2B
A3 A3A1 A3A2 A3B
B B A1 B A2 B A3
恰好选中1名男生和1名女生的概率为
18.(8分)【答案】(1);(2)每台雪炮每小时的出雪量为,每台雪枪每小时的出雪量为.
【解析】(1)如解图,过点D,C分别作AB的垂线,垂足分别为F,G,则四边形CDFG是矩形.
∴FG=CD=20m,CG=DF,.
∴∠CBG=∠ECB=30°.
在Rt△BCG中,,
∴.
在Rt△ADF中,∠DAF=75°,,
∴.
又∵AF+FG+BG=AB,AB=140m,
∴.
解得DF≈60.
答:大跳台出发区CD距离地面AB的高度约为60m.
(2)设每台雪炮每小时的出雪量为,则每台雪枪每小时的出雪量为.
根据题意,得,解得x=60.
经检验,x=60是原方程的解,且符合题意.
∴60-40=20().
答:每台雪炮每小时的出雪量为,每台雪枪每小时的出雪量为.
19.(10分)【答案】(1),;(2)6;(3)或
【解析】(1)解:∵轴于点D,
∴轴于点D,
,,
∴,即,
解得.
在Rt△ACD中,
∵,
∴.
∵点O是线段CD的中点,
∴,
∴,
∴反比例函数表达式为.
∵点B的坐标为
∴.
∴设一次函数表达式为,
则解得
∴一次函数解析式为.
(2)由(1),得.
(3)观察函数图象知,当时,
或.
20.(10分)【答案】(1)见解析;(2)见解析;(3)
【解析】(1)
证明:如图1,
连接AD,OD,
∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD,BD=CD,
∵OA=OD,
∴∠ODA=∠BAD,
∴∠ODA=∠CAD,
∵NM⊥AC,
∴∠AMN=90°,
∴∠DAC+∠ADM=90°,
∴∠ODA+∠ADM=90°,即∠ODM=90°,
∴OD⊥MN,
∴直线MN是⊙O的切线;
(2)证明:由(1)知,∠ADC=90°,BD=CD,
∴∠ADC=∠DMC=90°,
∵∠ACD=∠DCM,
∴△CMD∽△CDA,
∴,
∴CD2=AC CM,
∴BD2=AC CM,
在△BGD和△CMD中,,
∴△BGD≌△CMD(AAS),
∴BG=CM,
∴BD2=AC BG;
(3)解:如图2,
连接OD,OC,由(1)知∠ODN=90°,
∵OD=OB=BN=1,
∴cos∠DON=,
∴∠DON=60°,
∵OB=OD,
∴∠OBD=60°,
∵AB=AC,
∴△ABC是等边三角形,
∵OA=OB,
∴CO⊥AB,OC=AC sin60°=,
∴tan∠ANC=.
B卷
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
1.【答案】3
【解析】点是斜边的中点,且点的坐标为,
,即,
将点代入双曲线得:,
则双曲线的解析式为,
又,,且点在上,
,点的横坐标与点的横坐标相同,即为,
当时,,即,
,
则的面积为,故答案为:3.
2.【答案】2021
【解析】∵a、b是方程x2 +x- 2022 = 0的两根,
∴ a2+a- 2022 = 0, a+b= -1,
∴a2+a= 2022,
∴a2+ 2a+b=a2 +a+a+b= 2022-1=2021
故答案为:2021
3.【答案】或
【解析】作EF平行于MN,且与⊙O切,交x轴于点E,交y轴于点F,如图所示.
设直线EF的解析式为y=x+b,即x-y+b=0,
∵EF与⊙O相切,且⊙O的半径为1,
∴,
解得:b=或b=,
∴直线EF的解析式为或,
∴点E的坐标为(,0)或(,0).
令y=x2中y=0,则x=2,
∴点M(2,0).
∵根据运动的相对性,且⊙O以每秒1个单位的速度向右作平移运动,
∴移动的时间为秒或秒.
故答案为:或.
4.【答案】或
【解析】如图,①当点在对角线上时,点和点重合,如解图 1 所示.
,,
四边形是矩形,,
,
折叠,
,
②当点在对角线上时,连接,过点作于点, 过点 作 于点 , 如解 图 2 所示.
同理可得.
在 Rt 中,
.
.
.
综上所述, 线段 的长为 或 .故答案为:或
5.【答案】 255 21
【解析】(1)第一次,;第二次,;第三次,;
(2)第一次,;
第二次,;
第三次;
第四次,;
第五次,;
第六次,,所以.
故答案为(1)255;(2)21.
二、解答题(本大题共3个小题,共30分,答过程写在答题卡上)
6.(8分)【答案】(1)A种饮料调价前的单价为5元/瓶,B种饮料调价前的单价为6元/瓶
(2)n的最大值为601
【解析】(1)解:设A、B饮料在调价前每瓶各x元、y元,
根据题意得: 解得:
答:A种饮料调价前的单价为5元/瓶,B种饮料调价前的单价为6元/瓶;
(2)解:设购进A饮料m瓶,则购进B饮料2m瓶,购进C饮料(n-3m)瓶
根据题意得: 解得:n=481+0.6m
购买A、B两种饮料的钱数要少于3367元
解得:
又m、n均为整数
当m=200时,n取得最大值,最大值为601
答:n的最大值为601.
7.(10分)【答案】(1)1+;(2)M=DM,理由见解析;(3)=60°,理由见解析.
【解析】(1)解:∵四边形ABCD是矩形,
∴CD=AB,BC=DA,∠BAD=90°,
∵将矩形ABCD绕点A顺时针旋转90°得到矩形,
∴∠AD=∠BAD=90°,=CD=AB=2,
∴AB与A重合,即点A、B、在同一条直线上,
设BC=DA=A=x,则B=x﹣2,
∵∠=∠BAD=90°,∠B=∠ABD,
∴△B∽△∠ABD,
∴,
∴,
解得x1=1+,x2=1-(不符合题意,舍去),
∴BC=1+.
(2)解:M=DM,理由如下:
如图4,连结D,
∵A=AD,
∴∠AD=∠AD,
∵=AB,∠A=∠BAD=90°,A=DA,
∴△A≌△BAD(SAS),
∴∠A=∠ADB,
∵MA,
∴∠AM=∠A,
∴∠AM=∠ADB,
∴∠AD﹣∠AM=∠AD﹣∠ADB,
∴∠MD=∠MD,
∴M=DM.
(3)解:=60°,理由如下:
如图5,连结AM,
∵A=AD,M=DM,AM=AM,
∴△AM≌△ADM(SSS),
∴∠AM=∠ADM,∠MA=∠MAD=∠DA==30°,
∵∠AM=∠NA,
∴∠NA=∠ADM=30°,
∴∠NA+∠MA=∠ADM+∠MAD=60°,
∵∠NAM=∠NA+∠MA,∠NMA=∠ADM+∠MAD,
∴∠NAM=∠NMA,
∴MN=AN,
∴△AMN是等腰三角形,
∵∠NAM=∠NA+∠MA=60°,
∴△AMN是等边三角形.
8.(12分)【答案】(1);(2);(3)或
【解析】(1)解:∵抛物线交x轴交于和点,
设,
∵当x=0时,y=3,
∴,解得a=-1,
∴,即.
(2)解:设直线BC的解析式为:y=kx+b(k≠0),
∵B(3,0),C(0,3),
则 ,解得,
∴y=-x+3,
设D(m,-m+3),
∴E(m,-m2+2m+3),
∵DE= yE-yD=-m2+2m+3-(-m+3)=-m2+3m,
由(1)得,OB=OC=3,
∴△BOC为等腰直角三角形,
∵DE∥OC,EF∥OB,
∴△DEF为等腰直角三角形,
∴ ,
∵点E在点D的上方,
∴0
∴当 时,DE的最大值为 ,
∴的最大值为 ;
(3)解:如图,与直线相交与,连接ND,
∵BC是MN的对称轴,
∴ND=MD,
由(2)知△BOC是等腰直角三角形,
∴∠BDH=∠CBO=45°,
∴∠CDM=∠BDH=45°,
∴△MDN是等腰直角三角形,
∴抛物线的对称轴为 ,
设M(1,p),D(1,-1+3),即(1,2),
∵ND=MD=p-2,
当M点在D点上方时,
∴xN=1-(p-2)=-p+3,
∴N(-p+3, 2)
∵N点在抛物线上,
∴ ,
解得或(舍去),
∴N点坐标 ;
当M点在D点下方时,
同理得出为等腰直角三角形,
∴ ,
设的坐标为 ,
∴ ,
∴xN’=(2-q)+1=3-q,
∴N’(3-q, 2),
∵N’点在抛物线上,
∴ ,解得(舍去)或,
∴,
综上,N点坐标为或.
同课章节目录
