多项式除以单项式[下学期]
图片预览

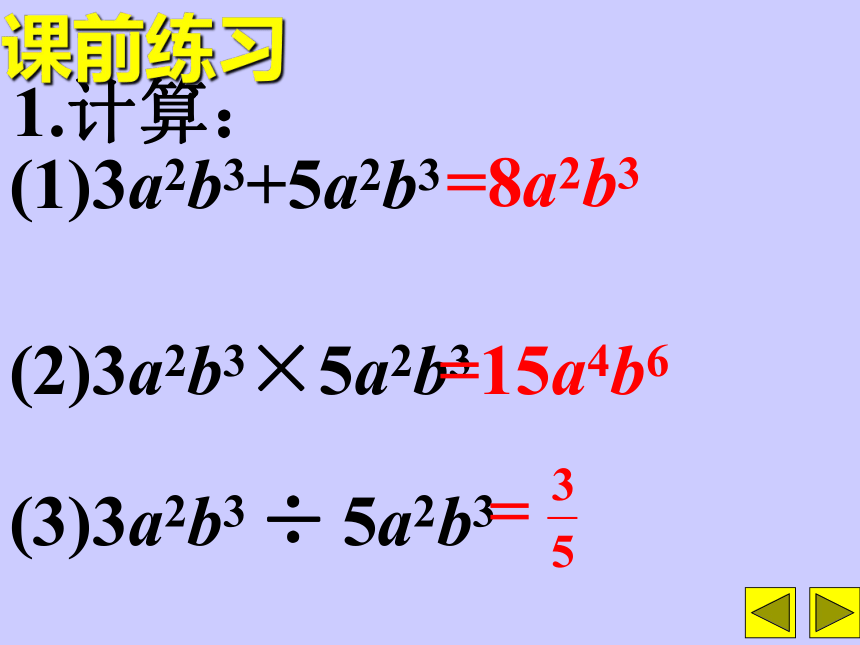





文档简介
课件19张PPT。多项式除以单项式整式的乘除 1.计算:课前练习(1)3a2b3+5a2b3(2)3a2b3×5a2b3(3)3a2b3 ÷ 5a2b3=8a2b3=15a4b6 2.计算:(1)(2x2-3x-1)?3x2单项式与多项式相乘的法则是什么?= 6x4-9x3-3x2单项式与多项式相乘单项式多项式相加 计算下列各式,并说说你是怎样计算的?m(a+b+c)= am+bm+cm =a+b+c(am+bm+cm)÷m多项式除以单项式=反之请说出多项式除以单项式的运算法则多项式除以单项式 多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。(am+bm+cm)÷m=am÷m+bm÷m+cm÷m例1.计算:解:(1)(12a3-8a2-3a)÷4a(2)(6a2b-2ab2-b3)÷(-3b)=12a3 ÷4a-8a2 ÷4a-3a ÷4a=-6a2b ÷3b+2ab2÷3b+b3÷3b2:化简解:=(4x2+4xy+y2-y2-4xy-8x)÷2x=(4x2-8x)÷2x=2x-4课堂练习1.计算:(1)(-8x+6)÷(-4)(3)(9a3b-12a2b2+8ab3)÷3ab(2)(6x2-9x)÷3x(4)(4x2y-8x3y3)÷(-2x2y)(5)(-7a4bc2+4a3b2-5a2b3)(6)( a6x3+ a9x4 ax5)÷(-2a2b)÷ ax3课堂总结 1、多项式除以单项式法则:多项式除以单项式,先把这个多项式的每一项除以这个多项式,再把所得的商相加。
2、应用法则转化多项式除以单项式为单项式除以单项式。 3、运算中应注意的问题:
(1)所除的商应写成最简的形式;
(2)除式与被除式不能交换;
4、整式混合运算要注意运算顺序,还要注意运用有关的运算公式和性质,使运算简便。 例2.计算:-15x2y3-(-27x6y3)]÷4x2y22.已知:f(x)=25x4 +15x3-20x2,求:(1) f(x)÷5x(2) f(x)÷(-10x2)3.已知:f(x)=25x4 +15x3-20x2,求:解:(1) f(x)÷5x=(25x4 +15x3-20x2)÷5x=5x3 +3x2-4x2.已知:f(x)=25x4 +15x3-20x2,求:(2) f(x)÷(-10x2)=(25x4 +15x3-20x2)÷(-10x2)= -2.5x2 –1.5x+22.已知:f(x)= -8x4 +3x3-2x2,(1) f(x)+g(x)g(x)= -4x2,求:(4) f(x)÷g(x)(2) f(x)-g(x)(3) f(x)?g(x) 2.计算:(1)[(-3xy)2?x3-2x3(3xy2)3? y]
÷9x4y2作业:第50页知识技能:第1题(5)(6)(7)(8)小题
2、应用法则转化多项式除以单项式为单项式除以单项式。 3、运算中应注意的问题:
(1)所除的商应写成最简的形式;
(2)除式与被除式不能交换;
4、整式混合运算要注意运算顺序,还要注意运用有关的运算公式和性质,使运算简便。 例2.计算:-15x2y3-(-27x6y3)]÷4x2y22.已知:f(x)=25x4 +15x3-20x2,求:(1) f(x)÷5x(2) f(x)÷(-10x2)3.已知:f(x)=25x4 +15x3-20x2,求:解:(1) f(x)÷5x=(25x4 +15x3-20x2)÷5x=5x3 +3x2-4x2.已知:f(x)=25x4 +15x3-20x2,求:(2) f(x)÷(-10x2)=(25x4 +15x3-20x2)÷(-10x2)= -2.5x2 –1.5x+22.已知:f(x)= -8x4 +3x3-2x2,(1) f(x)+g(x)g(x)= -4x2,求:(4) f(x)÷g(x)(2) f(x)-g(x)(3) f(x)?g(x) 2.计算:(1)[(-3xy)2?x3-2x3(3xy2)3? y]
÷9x4y2作业:第50页知识技能:第1题(5)(6)(7)(8)小题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
