8.3.1分类变量与列联表 课件(共23张PPT)
文档属性
| 名称 | 8.3.1分类变量与列联表 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 17:08:52 | ||
图片预览








文档简介
8.3.1 分类变量与列联表
8.3 列联表与独立性检验
知识文化
世界无烟日(World No Tobacco Day),是世界卫生组织在1987年创立的,第一个世界无烟日是1988年4月7日,自1989年起,世界无烟日改为每年的5月31日。为什么将世界无烟日改为5月 31日呢?是因为第二天是国际儿童节,希望下一代免受烟草危害。
世界无烟日的意义是宣扬不吸烟的观念。而每年皆会有一个中心主题。
2023年是第36个世界无烟日。
2019年世界无烟日的重点是“烟草和肺部健康”
吸烟是否会增加患肺癌的风险?怎样用数学知识说明呢?
基本概念——
1、分类变量:一种特殊的随机变量,以区别不同的现象或性质
例如:对于性别变量,其取值为男和女两种.
♂
♀
这种变量的不同“值”表示个体所属的不同类别.
性别、是否吸烟、是否患肺癌、宗教信仰、国籍等等都属于分类变量
体重、身高、温度、考试成绩等等这些变量属于
数值变量
变量
数值变量
分类变量
分类变量与数值变量之间的区别是什么?
基本概念——
变量
数值变量
分类变量
分类变量与数值变量之间的区别是什么?
例:体重、身高、温度、考试成绩等
数值变量的取值为实数.
其大小和运算都有实际含义.
两个数值变量之间的关系:回归分析法;
由一个变量的变化去推测另一个变量的变化
例:性别、是否吸烟、是否患肺癌、国籍等
分类变量的取值可以用实数来表示;
这些数值只作为编号使用,用来表示不同的类别;
并没有通常的大小和运算意义。
例如,学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示
本节我们主要讨论取值是{0,1}的分类变量的关联性问题.
基本概念——
2、2×2列联表
以左表为例, 2×2列联包含了X和Y的如下信息: 最后一行的前两个数分别是事件{Y=0}和{Y=1}中样本点的个数; 最后一列的前两个数分别是事件{X=0}和{X=1}中样本点的个数 ; 中间的四个格中的数是表格的核心部分, 给出了事件{X=x, Y=y}(x, y=0, 1)中样本点的个数; 右下角格中的数是样本空间中样本点的总数.
如上表这样,列出两个分类变量的频数表,称为列联表。
特别地,两个变量都只有两个结果,这样的列联表叫【2×2列联表】
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
牛刀小试:下面是一个2×2列联表,则表中????、????的值分别为( )
?
????
?
????
????
合计
????=????1
????=????2
7817
????=????1
????
21
????
????=????2
????
25
33
合计
????
????
106
{5940675A-B579-460E-94D1-54222C63F5DA}????.96,94
????.60,52
????.52,54
????.50,52
问题情境 为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,其中,不吸烟的7817人中42人患肺癌,吸烟的2148人中91人患肺癌,试分析吸烟是否对患肺癌有影响.
{5940675A-B579-460E-94D1-54222C63F5DA}
不患肺癌(Y=0)
患肺癌(Y=1)
总计
不吸烟(X=0)
吸烟(X=1)
总计
解:定义分类变量X和Y如下:
关于分类变量X和Y的2×2列联表如下:
如何判断两个分类变量之间是否具有关联性呢?
7775
2099
9874
42
49
91
7817
2148
9965
{5940675A-B579-460E-94D1-54222C63F5DA}
不患肺癌(Y=0)
患肺癌(Y=1)
总计
不吸烟(X=0)
7775
42
7817
吸烟(X=1)
2099
49
2148
总计
9874
91
9965
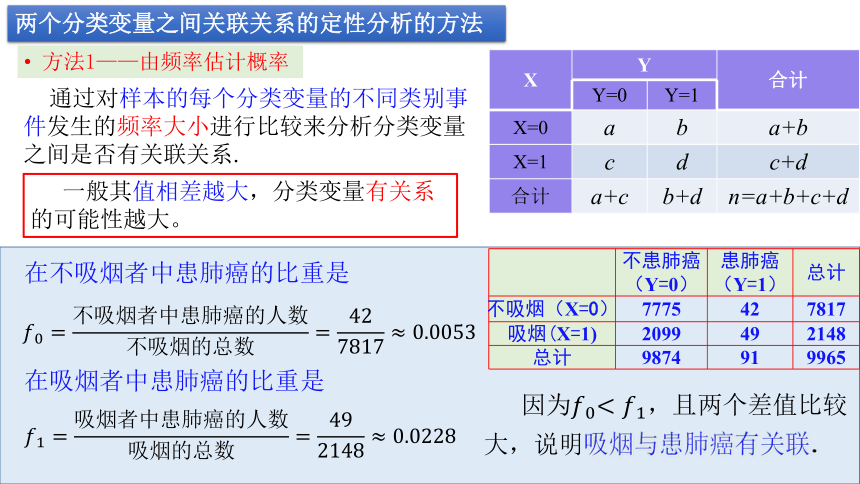
????0=不吸烟者中患肺癌的人数不吸烟的总数=427817≈0.0053
?
????1=吸烟者中患肺癌的人数吸烟的总数=492148≈0.0228
?
在不吸烟者中患肺癌的比重是
在吸烟者中患肺癌的比重是
因为????0?
两个分类变量之间关联关系的定性分析的方法
方法1——由频率估计概率
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.
一般其值相差越大,分类变量有关系的可能性越大。
{5940675A-B579-460E-94D1-54222C63F5DA}
不患肺癌(Y=0)
患肺癌(Y=1)
总计
不吸烟(X=0)
7775
42
7817
吸烟(X=1)
2099
49
2148
总计
9874
91
9965
两个分类变量之间关联关系的定性分析的方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
一般其值相差越大,分类变量有关系的可能性越大。
方法2——借助条件概率
如:利用已知数据分别来计算两个条件概率????(????=????|????=????)、????(????=????|????=????)并进行比较。
?
因为????????=????????=?????
两个分类变量之间关联关系的定性分析的方法
能够直观地反映出两个分类变量间是否相互影响。
方法3——借助等高堆积条形图
说明吸烟者中患肺癌的概率更高。
在吸烟者中患肺癌的比重是2.28%.
在不吸烟者中患肺癌的比重是0.54%.
牛刀小试:下列关于等高条形图的叙述正确的是( )
A.从等高条形图中可以精确地判断两个分类变量是否有关系
B.从等高条形图中可以看出两个变量频数的相对大小
C.从等高条形图中可以粗略地看出两个分类变量是否有关系
D.以上说法都不对
????
?
牛刀小试:如图是调查某地区男女中学生是否喜欢理科的等高条形图,从图中可以看出该地区的中学生( )
A.性别与是否喜欢理科无关
B.女生中喜欢理科的比例为80%
C.男生比女生喜欢理科的可能性大
D.男生中喜欢理科的比例为80%
????
?
定义一对分类变量X和Y如下:
例题1 为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查. 全校学生的普查数据如下: 523名女生中有331名经常锻炼;601名男生中有473名经常锻炼. 你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
解:
列2×2列联表
性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
192
331
523
男生(X=1)
128
473
601
合计
320
804
1124
性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
192
331
523
男生(X=1)
128
473
601
合计
320
804
1124
????0=经常锻炼的女生数女生总数=331523≈0.633
?
????1=经常锻炼的男生数男生总数=473601≈0.787
?
????1>????0
?
结论:该校的女生和男生在体育锻炼的经常性方面存在差异,男生更经常锻炼。
方法1——由频率估计概率
方法2——借助条件概率
????(????=1|????=0)=????(????=1,????=0)????(????=0)=331523≈0.633
?
????(????=1|????=1)=????(????=1,????=1)????(????=1)=473601≈0.787
?
????(????=1|????=1)>????(????=1|????=0)
?
方法3——借助等高堆积条形图
例题2 为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生. 通过测验得到了如下数据: 甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:定义分类变量X和Y如下:
列2×2列联表
学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
用等高堆积条形图直观地展示上述计算结果:
通过比较发现,两个学校学生抽样数据中数学成绩优秀的频率存在差异,甲校的频率明显高于乙校的频率.依据频率稳定于概率的原理,我们可以推断甲校学生数学成绩优秀的概率大于乙校学生数学成绩优秀的概率.
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
甲校
乙校
因此,可以认为两校学生的数学成绩优秀率存在差异,甲校学生的数学成绩优秀率比乙校学生的高.
学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
思考 你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
条件概率:P(Y=1|X=0)>P(Y=1|X=1)
思考 你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
事实上,“两校学生的数学成绩优秀率存在差异”这个结论是根据两个频率间存在差异推断出来的.
有可能出现这种情况: 在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.
对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
后面我们将讨论犯这种错误的概率大小问题.
有可能
课本127页
4. 假设在本小节“问题”(例1)中,只是随机抽取了44名学生,按照性别和体育锻炼情况整理为如下的列联表:
性别
锻炼
合计
不经常
经常
女生
5
15
20
男生
6
18
24
合计
11
33
44
(1) 据此推断性别因素是否影响学生锻炼的经常性;
(2) 说明你的推断结论是否可能犯错,并解释原因.
课本127页
性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
5
15
20
男生(X=1)
6
18
24
合计
11
33
44
(1) 据此推断性别因素是否影响学生锻炼的经常性;
(2) 说明你的推断结论是否可能犯错,并解释原因.
解: (1)根据列联表中的数据,计算得男女生中不经常锻炼和经常锻炼的频率分别为
通过对比发现,男生中不经常锻炼和经常锻炼的频率与女生中不经常锻炼和经常锻炼的频率分别相等,依据频率稳定于概率的原理,可以推断P(Y=1|X=0)=P(Y=1|X=1). 因此,可以认为性别对体育锻炼的经常性没有影响.
(2) 推断可能犯错误. 因为样本是通过随机抽样得到的,频率具有随机性,因此推断可能犯错误.
1.2×2列联表 —— 给出了两个分类变量数据的交叉分类频数
2.判断两个分类变量之间是否具有关联性的三种方法
图形分析法
频率分析法
条件概率法
这样得出的结论是否会出现错误呢?是由什么引起的?
课堂小结:
频率具有随机性,与概率之间存在差异
样本容量较小时,犯错误的概率较大
课本127页
1. 成语“名师出高徒”可以解释为“知名老师指导出高水平学生的概率较大”,即老师的名声与学生的水平之间有关联. 你能举出更多的描述生活中两种属性或现象之间关联的成语吗?
解:例如水涨船高、登高望远等.
课本127页
2. 例1中的随机抽样数据是否足够确定与X和Y有关的所有概率和条件概率?为什么?
解:不能. 因为随机抽样得到的样本具有随机性,根据样本数据计算出来的频率也具有随机性. 在统计推断中,依据频率稳定于概率的原理,可以利用频率推断与X和Y有关的概率和条件概率,但由于频率具有随机性,这种推断可能犯错误. 因此,随机抽样数据不足以确定与X和Y有关的所有概率和条件概率.
课本127页
3. 根据有关规定,香烟盒上必须印上“吸烟有害健康”的警示语. 那么
(1) 吸烟是否对每位烟民一定会引发健康问题?
(2) 有人说吸烟不一定引起健康问题,因此可以吸烟. 这种说法对吗?
解:(1) 从已掌握的知识来看,吸烟会损害身体的健康. 但除了吸烟之外,身体的健康还受许多其他随机因素的影响,它是很多因素共同作用的结果. 吸烟导致患病的案例非常普遍,但也可以找到长寿的吸烟者. 因此健康与吸烟有关联,即从统计意义上讲,吸烟会损害健康,但不一定会对每位烟民都引起健康问题.
(2) 这种说法不正确. 虽然吸烟不一定会对每个人都引起健康问题,但根据统计数据,吸烟比不吸烟引起健康问题的可能性大,因此“吸烟不一定引起健康问题,因此可以吸烟”的说法是不对的.
8.3 列联表与独立性检验
知识文化
世界无烟日(World No Tobacco Day),是世界卫生组织在1987年创立的,第一个世界无烟日是1988年4月7日,自1989年起,世界无烟日改为每年的5月31日。为什么将世界无烟日改为5月 31日呢?是因为第二天是国际儿童节,希望下一代免受烟草危害。
世界无烟日的意义是宣扬不吸烟的观念。而每年皆会有一个中心主题。
2023年是第36个世界无烟日。
2019年世界无烟日的重点是“烟草和肺部健康”
吸烟是否会增加患肺癌的风险?怎样用数学知识说明呢?
基本概念——
1、分类变量:一种特殊的随机变量,以区别不同的现象或性质
例如:对于性别变量,其取值为男和女两种.
♂
♀
这种变量的不同“值”表示个体所属的不同类别.
性别、是否吸烟、是否患肺癌、宗教信仰、国籍等等都属于分类变量
体重、身高、温度、考试成绩等等这些变量属于
数值变量
变量
数值变量
分类变量
分类变量与数值变量之间的区别是什么?
基本概念——
变量
数值变量
分类变量
分类变量与数值变量之间的区别是什么?
例:体重、身高、温度、考试成绩等
数值变量的取值为实数.
其大小和运算都有实际含义.
两个数值变量之间的关系:回归分析法;
由一个变量的变化去推测另一个变量的变化
例:性别、是否吸烟、是否患肺癌、国籍等
分类变量的取值可以用实数来表示;
这些数值只作为编号使用,用来表示不同的类别;
并没有通常的大小和运算意义。
例如,学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示
本节我们主要讨论取值是{0,1}的分类变量的关联性问题.
基本概念——
2、2×2列联表
以左表为例, 2×2列联包含了X和Y的如下信息: 最后一行的前两个数分别是事件{Y=0}和{Y=1}中样本点的个数; 最后一列的前两个数分别是事件{X=0}和{X=1}中样本点的个数 ; 中间的四个格中的数是表格的核心部分, 给出了事件{X=x, Y=y}(x, y=0, 1)中样本点的个数; 右下角格中的数是样本空间中样本点的总数.
如上表这样,列出两个分类变量的频数表,称为列联表。
特别地,两个变量都只有两个结果,这样的列联表叫【2×2列联表】
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
牛刀小试:下面是一个2×2列联表,则表中????、????的值分别为( )
?
????
?
????
????
合计
????=????1
????=????2
7817
????=????1
????
21
????
????=????2
????
25
33
合计
????
????
106
{5940675A-B579-460E-94D1-54222C63F5DA}????.96,94
????.60,52
????.52,54
????.50,52
问题情境 为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,其中,不吸烟的7817人中42人患肺癌,吸烟的2148人中91人患肺癌,试分析吸烟是否对患肺癌有影响.
{5940675A-B579-460E-94D1-54222C63F5DA}
不患肺癌(Y=0)
患肺癌(Y=1)
总计
不吸烟(X=0)
吸烟(X=1)
总计
解:定义分类变量X和Y如下:
关于分类变量X和Y的2×2列联表如下:
如何判断两个分类变量之间是否具有关联性呢?
7775
2099
9874
42
49
91
7817
2148
9965
{5940675A-B579-460E-94D1-54222C63F5DA}
不患肺癌(Y=0)
患肺癌(Y=1)
总计
不吸烟(X=0)
7775
42
7817
吸烟(X=1)
2099
49
2148
总计
9874
91
9965
????0=不吸烟者中患肺癌的人数不吸烟的总数=427817≈0.0053
?
????1=吸烟者中患肺癌的人数吸烟的总数=492148≈0.0228
?
在不吸烟者中患肺癌的比重是
在吸烟者中患肺癌的比重是
因为????0?
两个分类变量之间关联关系的定性分析的方法
方法1——由频率估计概率
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.
一般其值相差越大,分类变量有关系的可能性越大。
{5940675A-B579-460E-94D1-54222C63F5DA}
不患肺癌(Y=0)
患肺癌(Y=1)
总计
不吸烟(X=0)
7775
42
7817
吸烟(X=1)
2099
49
2148
总计
9874
91
9965
两个分类变量之间关联关系的定性分析的方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
一般其值相差越大,分类变量有关系的可能性越大。
方法2——借助条件概率
如:利用已知数据分别来计算两个条件概率????(????=????|????=????)、????(????=????|????=????)并进行比较。
?
因为????????=????????=?????
两个分类变量之间关联关系的定性分析的方法
能够直观地反映出两个分类变量间是否相互影响。
方法3——借助等高堆积条形图
说明吸烟者中患肺癌的概率更高。
在吸烟者中患肺癌的比重是2.28%.
在不吸烟者中患肺癌的比重是0.54%.
牛刀小试:下列关于等高条形图的叙述正确的是( )
A.从等高条形图中可以精确地判断两个分类变量是否有关系
B.从等高条形图中可以看出两个变量频数的相对大小
C.从等高条形图中可以粗略地看出两个分类变量是否有关系
D.以上说法都不对
????
?
牛刀小试:如图是调查某地区男女中学生是否喜欢理科的等高条形图,从图中可以看出该地区的中学生( )
A.性别与是否喜欢理科无关
B.女生中喜欢理科的比例为80%
C.男生比女生喜欢理科的可能性大
D.男生中喜欢理科的比例为80%
????
?
定义一对分类变量X和Y如下:
例题1 为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查. 全校学生的普查数据如下: 523名女生中有331名经常锻炼;601名男生中有473名经常锻炼. 你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
解:
列2×2列联表
性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
192
331
523
男生(X=1)
128
473
601
合计
320
804
1124
性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
192
331
523
男生(X=1)
128
473
601
合计
320
804
1124
????0=经常锻炼的女生数女生总数=331523≈0.633
?
????1=经常锻炼的男生数男生总数=473601≈0.787
?
????1>????0
?
结论:该校的女生和男生在体育锻炼的经常性方面存在差异,男生更经常锻炼。
方法1——由频率估计概率
方法2——借助条件概率
????(????=1|????=0)=????(????=1,????=0)????(????=0)=331523≈0.633
?
????(????=1|????=1)=????(????=1,????=1)????(????=1)=473601≈0.787
?
????(????=1|????=1)>????(????=1|????=0)
?
方法3——借助等高堆积条形图
例题2 为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生. 通过测验得到了如下数据: 甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:定义分类变量X和Y如下:
列2×2列联表
学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
用等高堆积条形图直观地展示上述计算结果:
通过比较发现,两个学校学生抽样数据中数学成绩优秀的频率存在差异,甲校的频率明显高于乙校的频率.依据频率稳定于概率的原理,我们可以推断甲校学生数学成绩优秀的概率大于乙校学生数学成绩优秀的概率.
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
甲校
乙校
因此,可以认为两校学生的数学成绩优秀率存在差异,甲校学生的数学成绩优秀率比乙校学生的高.
学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
思考 你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
条件概率:P(Y=1|X=0)>P(Y=1|X=1)
思考 你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
事实上,“两校学生的数学成绩优秀率存在差异”这个结论是根据两个频率间存在差异推断出来的.
有可能出现这种情况: 在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.
对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
后面我们将讨论犯这种错误的概率大小问题.
有可能
课本127页
4. 假设在本小节“问题”(例1)中,只是随机抽取了44名学生,按照性别和体育锻炼情况整理为如下的列联表:
性别
锻炼
合计
不经常
经常
女生
5
15
20
男生
6
18
24
合计
11
33
44
(1) 据此推断性别因素是否影响学生锻炼的经常性;
(2) 说明你的推断结论是否可能犯错,并解释原因.
课本127页
性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
5
15
20
男生(X=1)
6
18
24
合计
11
33
44
(1) 据此推断性别因素是否影响学生锻炼的经常性;
(2) 说明你的推断结论是否可能犯错,并解释原因.
解: (1)根据列联表中的数据,计算得男女生中不经常锻炼和经常锻炼的频率分别为
通过对比发现,男生中不经常锻炼和经常锻炼的频率与女生中不经常锻炼和经常锻炼的频率分别相等,依据频率稳定于概率的原理,可以推断P(Y=1|X=0)=P(Y=1|X=1). 因此,可以认为性别对体育锻炼的经常性没有影响.
(2) 推断可能犯错误. 因为样本是通过随机抽样得到的,频率具有随机性,因此推断可能犯错误.
1.2×2列联表 —— 给出了两个分类变量数据的交叉分类频数
2.判断两个分类变量之间是否具有关联性的三种方法
图形分析法
频率分析法
条件概率法
这样得出的结论是否会出现错误呢?是由什么引起的?
课堂小结:
频率具有随机性,与概率之间存在差异
样本容量较小时,犯错误的概率较大
课本127页
1. 成语“名师出高徒”可以解释为“知名老师指导出高水平学生的概率较大”,即老师的名声与学生的水平之间有关联. 你能举出更多的描述生活中两种属性或现象之间关联的成语吗?
解:例如水涨船高、登高望远等.
课本127页
2. 例1中的随机抽样数据是否足够确定与X和Y有关的所有概率和条件概率?为什么?
解:不能. 因为随机抽样得到的样本具有随机性,根据样本数据计算出来的频率也具有随机性. 在统计推断中,依据频率稳定于概率的原理,可以利用频率推断与X和Y有关的概率和条件概率,但由于频率具有随机性,这种推断可能犯错误. 因此,随机抽样数据不足以确定与X和Y有关的所有概率和条件概率.
课本127页
3. 根据有关规定,香烟盒上必须印上“吸烟有害健康”的警示语. 那么
(1) 吸烟是否对每位烟民一定会引发健康问题?
(2) 有人说吸烟不一定引起健康问题,因此可以吸烟. 这种说法对吗?
解:(1) 从已掌握的知识来看,吸烟会损害身体的健康. 但除了吸烟之外,身体的健康还受许多其他随机因素的影响,它是很多因素共同作用的结果. 吸烟导致患病的案例非常普遍,但也可以找到长寿的吸烟者. 因此健康与吸烟有关联,即从统计意义上讲,吸烟会损害健康,但不一定会对每位烟民都引起健康问题.
(2) 这种说法不正确. 虽然吸烟不一定会对每个人都引起健康问题,但根据统计数据,吸烟比不吸烟引起健康问题的可能性大,因此“吸烟不一定引起健康问题,因此可以吸烟”的说法是不对的.
