用推理的方法研究三角形(2)[下学期]
文档属性
| 名称 | 用推理的方法研究三角形(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-10 09:24:00 | ||
图片预览


文档简介
课件13张PPT。用推理的方法研究三角形(2)学习目标:1.巩固等腰三角形的判定定理和
性质定理.2.掌握等腰三角形三线合一性质.3.能综合运用等腰三角形的判定
定理、性质定理和三线合一来证
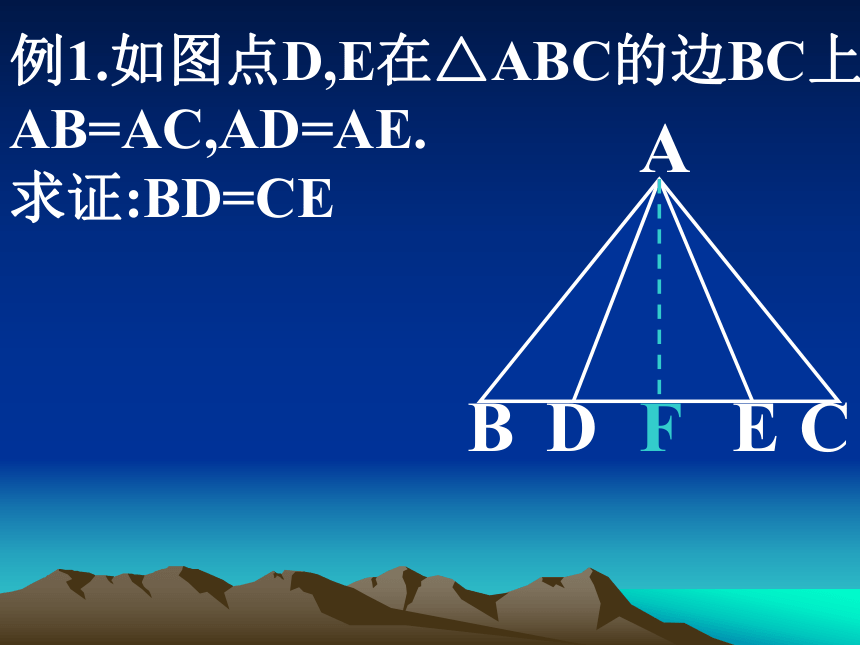
明问题例1.如图点D,E在△ABC的边BC上,
AB=AC,AD=AE.
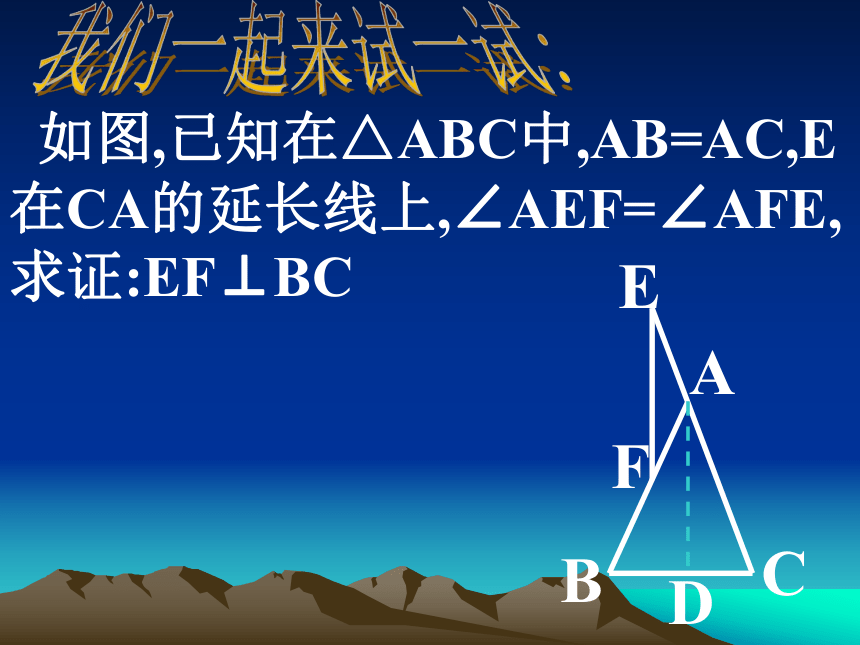
求证:BD=CEABCDEF我们一起来试一试: 如图,已知在△ABC中,AB=AC,E
在CA的延长线上,∠AEF=∠AFE,
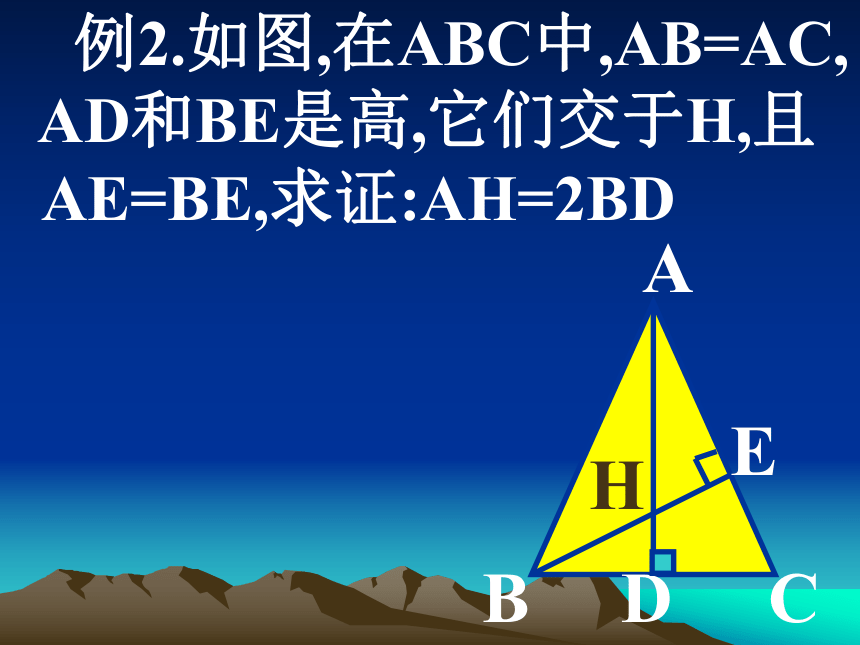
求证:EF⊥BCABCEFD 例2.如图,在ABC中,AB=AC,
AD和BE是高,它们交于H,且
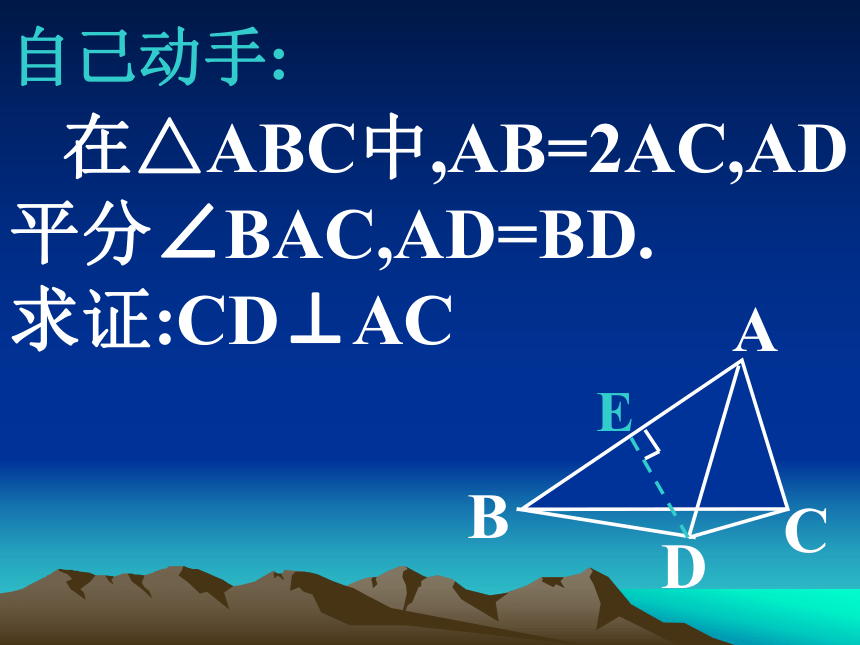
AE=BE,求证:AH=2BDABCDEH自己动手: 在△ABC中,AB=2AC,AD
平分∠BAC,AD=BD.
求证:CD⊥ACABCD例3.如图,AB=AC,BD⊥AC于点D,
CE⊥AB于E,BD,CE相交于F.
求证:AF平分∠BACABCDEF请你判断:阅读下题证明过程:已知:如图,D是△ABC中BC边上的上点,E
是AD上一点,EB=EC, ∠BAE=∠CAE,
求证:∠ABE=∠ACE证明:在△ABE和△ACE中EB=CE(已知)∠BAE=∠CAE(已知)AE=AE(公共边)∴△ABE≌△ACE----------第一步∴∠ABE=∠ACE----------第二步上面的证明边程是否正确?若正确,请写出
每一步推理的依据,若不正确,请指出错在
哪一步,并写出你认为正确的证明过程.ABCDE MN专项练习1.判断题:(1)两条直角边对应相等的两面个直角
三角形全等.( )(2)一条边和一个锐角对应相等的两个
直角三角形全等.( )(3)有两条边对应相等的两个直角三角
形全等.( )(4)有一角和一边对应相等的两个直角
三角形全等.( )(5)有两边相等的两个直角三角形全等.√√√( )××2.如图,在△ABC中,AB=AC,O是
△ABC内一点,且∠1=∠2.
求证:AO⊥BCABC12O3.如图, △ABC中,AD是高,CE是中
线,DC=BE,DG⊥CE,G是垂足.
求证:(1)G是CE中点.
(2) ∠B=2∠BCEABCDEG4.如图,在△ABC中,AB=AC,
∠BAC=120°,AC的垂直平分
线EF交AC于点E,交BC于点F.
求证:BF=2CFABCEF
性质定理.2.掌握等腰三角形三线合一性质.3.能综合运用等腰三角形的判定
定理、性质定理和三线合一来证
明问题例1.如图点D,E在△ABC的边BC上,
AB=AC,AD=AE.
求证:BD=CEABCDEF我们一起来试一试: 如图,已知在△ABC中,AB=AC,E
在CA的延长线上,∠AEF=∠AFE,
求证:EF⊥BCABCEFD 例2.如图,在ABC中,AB=AC,
AD和BE是高,它们交于H,且
AE=BE,求证:AH=2BDABCDEH自己动手: 在△ABC中,AB=2AC,AD
平分∠BAC,AD=BD.
求证:CD⊥ACABCD例3.如图,AB=AC,BD⊥AC于点D,
CE⊥AB于E,BD,CE相交于F.
求证:AF平分∠BACABCDEF请你判断:阅读下题证明过程:已知:如图,D是△ABC中BC边上的上点,E
是AD上一点,EB=EC, ∠BAE=∠CAE,
求证:∠ABE=∠ACE证明:在△ABE和△ACE中EB=CE(已知)∠BAE=∠CAE(已知)AE=AE(公共边)∴△ABE≌△ACE----------第一步∴∠ABE=∠ACE----------第二步上面的证明边程是否正确?若正确,请写出
每一步推理的依据,若不正确,请指出错在
哪一步,并写出你认为正确的证明过程.ABCDE MN专项练习1.判断题:(1)两条直角边对应相等的两面个直角
三角形全等.( )(2)一条边和一个锐角对应相等的两个
直角三角形全等.( )(3)有两条边对应相等的两个直角三角
形全等.( )(4)有一角和一边对应相等的两个直角
三角形全等.( )(5)有两边相等的两个直角三角形全等.√√√( )××2.如图,在△ABC中,AB=AC,O是
△ABC内一点,且∠1=∠2.
求证:AO⊥BCABC12O3.如图, △ABC中,AD是高,CE是中
线,DC=BE,DG⊥CE,G是垂足.
求证:(1)G是CE中点.
(2) ∠B=2∠BCEABCDEG4.如图,在△ABC中,AB=AC,
∠BAC=120°,AC的垂直平分
线EF交AC于点E,交BC于点F.
求证:BF=2CFABCEF
