17章第二节的一课一练[下学期]
图片预览



文档简介
第二节(2-3个课时)
第一课时
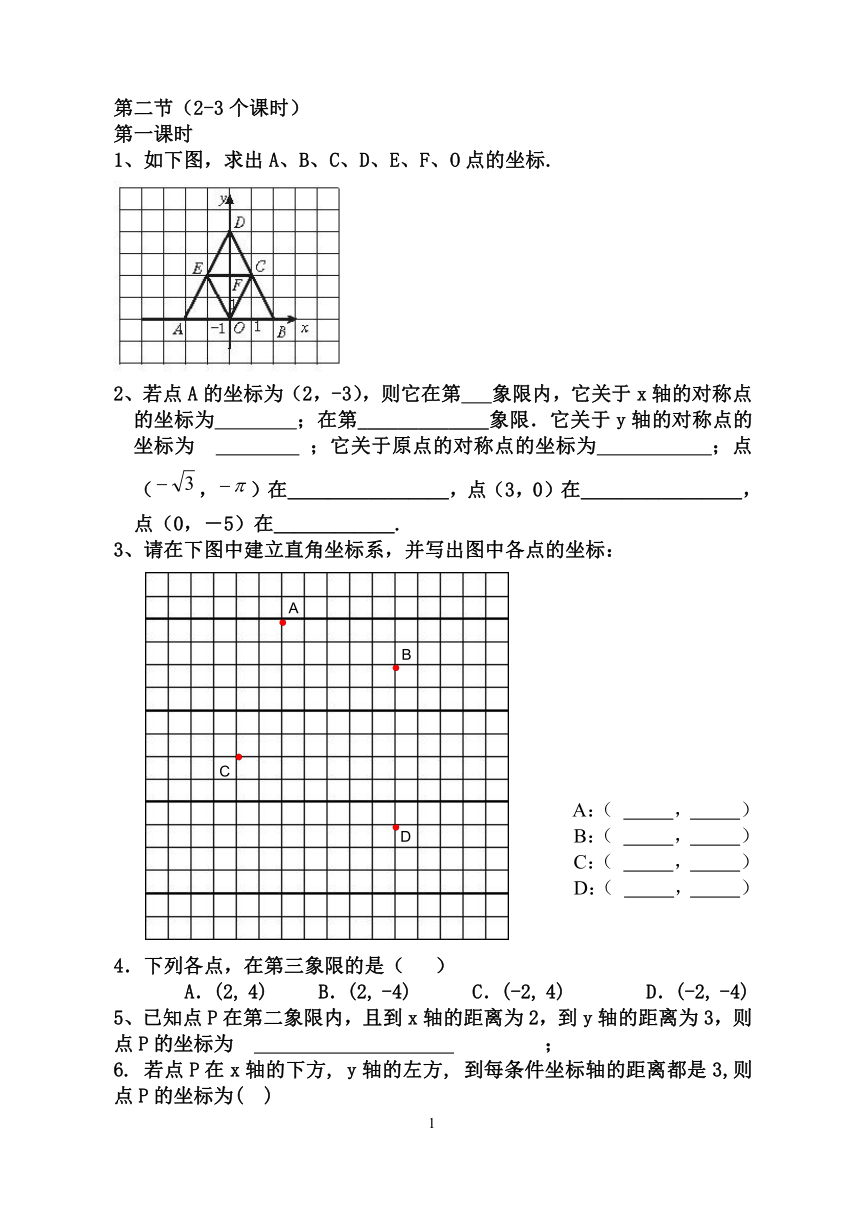
1、如下图,求出A、B、C、D、E、F、O点的坐标.
2、若点A的坐标为(2,-3),则它在第 象限内,它关于x轴的对称点的坐标为 ;在第_____________象限.它关于y轴的对称点的坐标为 ;它关于原点的对称点的坐标为 ;点(,)在________,点(3,0)在________,点(0,-5)在______.
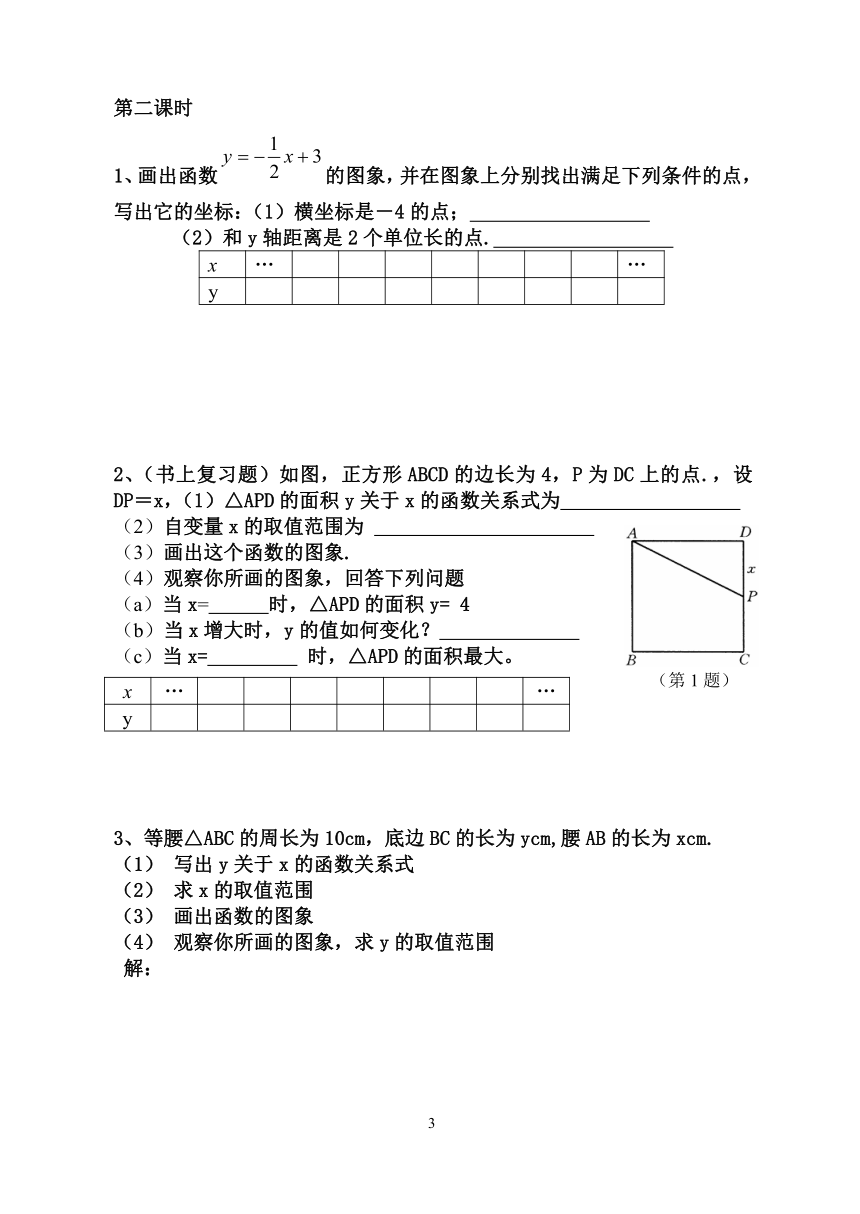
3、请在下图中建立直角坐标系,并写出图中各点的坐标:
A:( , )
B:( , )
C:( , )
D:( , )
4.下列各点,在第三象限的是( )
A.(2, 4) B.(2, -4) C.(-2, 4) D.(-2, -4)
5、已知点P在第二象限内,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为 ;
6. 若点P在x轴的下方, y轴的左方, 到每条件坐标轴的距离都是3,则点P的坐标为( )
A. (3,3) B. (-3,3) C. (-3,-3) D. (3,-3).
7. 点A在轴上,距离原点4个单位长度,则A点的坐标是( ) .
8. 在坐标系中, 点C(-2,3)向左平移3个单位长度后坐标为( )
9. 点P(x,y)在第四象限,|x|=1,|y|=3,则P点的坐标是 ( )
A.(1,3) B. (-1,3) C. (-1,-3) D. (1,-3)
[B组]
9、 已知A(a–1,3)在y轴上,则a = .
10、 13、在直角坐标系中,点(2x-6,x-5)在第四象限,则x的取值范围是__。A、3<x<5 B、-3<x<5 C、-5<x<3 D、-5<x<-3
11、(1)在平面直角坐标系中的点与有序实数对之间成___关系.
(2)如果点P(x,y)的坐标满足xy>0,那么点P在__ 象限,如果满足xy= 0,那么点P__________.
(3)如果点P(m-2,m-3)在第四象限,那么m的取值范围是____ .
(4)若点(m,2)与(3, n)关于原点对称,则m+n的值是 ____ .
(5) 已知线段AB的两个端点的坐标分别是A(3,4),B(-2,1),求:
①把线段AB向右平移2个单位后的线段的两个端点坐标;__
②线段AB关于x轴对称图形的两个端点的坐标;__
③线段AB关于Y轴对称图形的两个端点的坐标;__
[C组]
12.平面直角坐标系内,已知点P(a ,b)且ab<0,则点P在第__象限。
13、如果点M(a+b,ab)在第二象限,则点N(a,b)在第__象限。
14、平面直角坐标系中,点A(n,1-n)一定不在( C )
A 第一象限 B 第二象限 C 第三象限 D 第四象限
15:已知:点、、的坐标分别为、、,求△的面积.
16、若点P(a,b)在第四象限,则点M(b-a,a-b)在第__象限。
17、已知点P在第二象限,它的横坐标与纵坐标的和为1,点P的坐标可以是__(填上一个你认为正确的即可)
第二课时
1、画出函数的图象,并在图象上分别找出满足下列条件的点,写出它的坐标:(1)横坐标是-4的点;
(2)和y轴距离是2个单位长的点.
x … …
y
2、(书上复习题)如图,正方形ABCD的边长为4,P为DC上的点.,设DP=x,(1)△APD的面积y关于x的函数关系式为
(2)自变量x的取值范围为
(3)画出这个函数的图象.
(4)观察你所画的图象,回答下列问题
(a)当x= 时,△APD的面积y= 4
(b)当x增大时,y的值如何变化?
(c)当x= 时,△APD的面积最大。
x … …
y
3、等腰△ABC的周长为10cm,底边BC的长为ycm,腰AB的长为xcm.
(1) 写出y关于x的函数关系式
(2) 求x的取值范围
(3) 画出函数的图象
(4) 观察你所画的图象,求y的取值范围
解:
4、下列哪些点在函数的图象上?为什么?哪些不在?为什么?
A(1,-1)、B(0,2)、C(-1,-2)、D(2,0)、E(6,8)、F(-1,-3)
5、下列各点不在函数 的图象上的是( )
A、 B、 C、 D、
6、点 中,在函数 的图象上的点有( )
A、1个 B、2个 C、3个 D、4个
7、函数 的图象过四个点 中的( )
A、1个 B、2个 C、3个 D、4个
8、下列函数中,图象经过原点的为( )
A.y=5x+1 B.y=-5x-1
C.y=- D.y=
[B组]
9、点(a,6),在函数y=的图象上,则a=
10、数y=kx+5的图象经过(1,-2),则k=
[C组]
11、别在同一坐标系内画出各组函数的图象,并观察每组图象之间的关系和区别.
(1)
12、知函数
(1)画出这个函数的图象;
(2)写出相应的函数与x轴交点坐标,与y轴的交点坐标;
(3)判断点 是否在这个函数的图象上,如果在将它画在图象上.
13、若点 在函数 的图象上,且当 时, .
(1)求a、c的值;
(2)如果点(-1,m)和点(n ,6)也在函数的图象上,求m ,n的值.
第三课时
1、一天,亮亮发烧了,早晨他烧得很厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜,亮亮才感觉身上不那么发烫了,下面各图能基本上反映出亮亮这一天(0时-24时)体温的变化情况的是( )
2、星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离与散步的时间t(分)之间的函数关系,依据图象,下面描述符合小红散步情景的是( )
A从家出发,到一个公共阅报栏看了一
会儿报,就回家了。
B从家出发,到一个公共阅报栏看了一
会儿报,继续向前走了一段,然后回家了。
C 从家出发,一直散步(没有停留),然
后回家了。
D从家出发,散了一会儿步,就找同学去
了,18分钟后才开始返回。
3、如果A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
A A比B先出发 B A、B两人的速度相同
C A先到达终点 D B比A跑的路程多
4、丹家距学校m千米,一天她从家上学先以a千米/时的速度跑步锻炼前进,后以匀速b千米/时步行到达学校,共用n小时图17-2-12份中能够反映李丹同学距学校的距离s(千米)与上学的时间t(小时)之间的大致图象是 ( )
5、汽车在行驶过程中,速度往往是变化的,下图图象表示的是一辆汽车的速度随时间变化而变化的情况。
(1) 汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2) 汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3) 出发后8分钟到10分钟辶间可能发生了什么情况?
6、如图,图中直线AB、CD分别表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港的过程中,路程(km)随时间(小时)变化的图象(其中,轮船出发的时间记作0).
(1)分别求出轮船和快艇行驶过程中与间的函数关系式;
(2)求轮船和快艇行驶时的速度分别是多少;
(3)由图中哪点可以得知,快艇出发多少时间赶上轮船,
为什么?
(4)若用函数关系式来解决问题(3),你会怎样做?
为什么?
(4) 结合以上问题和你对图示中点A、B、C、D、E的理解,用一段话描述一下事情的经过.
7、如图表示某学校秋游活动时,学生乘坐旅游车所行走的路程与时间的关系的示意图,请根据示意田回答下列问题:
1.学生何时下车参观第一风景区 参观时间有多长
2.11:00时该车离开学校有多远
3.学生何时返回学校,返回学校时车的平均速度是多少
[B组]
8、小刚,爸爸,爷爷同时从家中出发到达同一目的地后又立即返回,小刚去时骑自行车,返回时步行;爷爷去时步行,返回时骑自行车;爸爸往返都步行。三人步行的速度不等,小刚与爷爷骑自行车的速度相等,每个人走的路程与时间的关系分别如下图中的一个,走完一个往返,小刚用 min,爸爸用 min,爷爷用 min。
9、小明为了表示爷爷吃过晚饭后,出门散步、报亭看报、回家的过程,绘制了爷爷离家的路程S(米)与外出的时间(分)之间的关系图(如图17-1-3所示),请根据这个关系图回答下列问题.
(1) 这个关系图反映了哪几个变量之间的关系?
(2) 任取变量t的一个值,变量S有几个值与它对应,变S是t的函数吗?
(3) 报亭离爷爷家多远?爷爷在报亭看了多长时间的报?
(4) 爷爷出门、返回的平均速度分别是多少?
10、在下列几个图象下的括号内分别填上对应函数的序号:(1)一杯越晾越凉的水(水温与时间的关系)(2)一面冉冉上升的旗子(高度与时间的关系)(3)足球守门员大脚开出去的球(高度与时间的关系)(4)匀速行驶的汽车(速度与时间的关系)
[C组]
11、如图所示是某蓄水池的横断面示意图,分深水区
和浅水区,如果这个蓄水池以固定的流量注水,下
面哪个图象能大致表示水的最大深度h与注水时间t
间的函数关系( )
12、沿墙用长32米的竹篱笆围成一个矩形的护栏(三面),设矩形的宽为x m,求矩形的面积s与x的函数关系式,画出此函数的图象,并指出当x为何值时面积最大?最大面积是多少?
13、一函数的图象如下图,根据图象:观察下图回答下列问题:
(1)确定自变量x的取值范围;
(2)求当 时,y的值;
(3)求当 时,对应的x的值;
(4)当x为何值时,函数值y最大?
(5)当x为何值时,函数值y最小?
(6)当y随x的增大而增大时,求相应的x值在什么范围内?
(7)当y随x的增大而减小时,求相应的x值在什么范围内?
PAGE
1
第一课时
1、如下图,求出A、B、C、D、E、F、O点的坐标.
2、若点A的坐标为(2,-3),则它在第 象限内,它关于x轴的对称点的坐标为 ;在第_____________象限.它关于y轴的对称点的坐标为 ;它关于原点的对称点的坐标为 ;点(,)在________,点(3,0)在________,点(0,-5)在______.
3、请在下图中建立直角坐标系,并写出图中各点的坐标:
A:( , )
B:( , )
C:( , )
D:( , )
4.下列各点,在第三象限的是( )
A.(2, 4) B.(2, -4) C.(-2, 4) D.(-2, -4)
5、已知点P在第二象限内,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为 ;
6. 若点P在x轴的下方, y轴的左方, 到每条件坐标轴的距离都是3,则点P的坐标为( )
A. (3,3) B. (-3,3) C. (-3,-3) D. (3,-3).
7. 点A在轴上,距离原点4个单位长度,则A点的坐标是( ) .
8. 在坐标系中, 点C(-2,3)向左平移3个单位长度后坐标为( )
9. 点P(x,y)在第四象限,|x|=1,|y|=3,则P点的坐标是 ( )
A.(1,3) B. (-1,3) C. (-1,-3) D. (1,-3)
[B组]
9、 已知A(a–1,3)在y轴上,则a = .
10、 13、在直角坐标系中,点(2x-6,x-5)在第四象限,则x的取值范围是__。A、3<x<5 B、-3<x<5 C、-5<x<3 D、-5<x<-3
11、(1)在平面直角坐标系中的点与有序实数对之间成___关系.
(2)如果点P(x,y)的坐标满足xy>0,那么点P在__ 象限,如果满足xy= 0,那么点P__________.
(3)如果点P(m-2,m-3)在第四象限,那么m的取值范围是____ .
(4)若点(m,2)与(3, n)关于原点对称,则m+n的值是 ____ .
(5) 已知线段AB的两个端点的坐标分别是A(3,4),B(-2,1),求:
①把线段AB向右平移2个单位后的线段的两个端点坐标;__
②线段AB关于x轴对称图形的两个端点的坐标;__
③线段AB关于Y轴对称图形的两个端点的坐标;__
[C组]
12.平面直角坐标系内,已知点P(a ,b)且ab<0,则点P在第__象限。
13、如果点M(a+b,ab)在第二象限,则点N(a,b)在第__象限。
14、平面直角坐标系中,点A(n,1-n)一定不在( C )
A 第一象限 B 第二象限 C 第三象限 D 第四象限
15:已知:点、、的坐标分别为、、,求△的面积.
16、若点P(a,b)在第四象限,则点M(b-a,a-b)在第__象限。
17、已知点P在第二象限,它的横坐标与纵坐标的和为1,点P的坐标可以是__(填上一个你认为正确的即可)
第二课时
1、画出函数的图象,并在图象上分别找出满足下列条件的点,写出它的坐标:(1)横坐标是-4的点;
(2)和y轴距离是2个单位长的点.
x … …
y
2、(书上复习题)如图,正方形ABCD的边长为4,P为DC上的点.,设DP=x,(1)△APD的面积y关于x的函数关系式为
(2)自变量x的取值范围为
(3)画出这个函数的图象.
(4)观察你所画的图象,回答下列问题
(a)当x= 时,△APD的面积y= 4
(b)当x增大时,y的值如何变化?
(c)当x= 时,△APD的面积最大。
x … …
y
3、等腰△ABC的周长为10cm,底边BC的长为ycm,腰AB的长为xcm.
(1) 写出y关于x的函数关系式
(2) 求x的取值范围
(3) 画出函数的图象
(4) 观察你所画的图象,求y的取值范围
解:
4、下列哪些点在函数的图象上?为什么?哪些不在?为什么?
A(1,-1)、B(0,2)、C(-1,-2)、D(2,0)、E(6,8)、F(-1,-3)
5、下列各点不在函数 的图象上的是( )
A、 B、 C、 D、
6、点 中,在函数 的图象上的点有( )
A、1个 B、2个 C、3个 D、4个
7、函数 的图象过四个点 中的( )
A、1个 B、2个 C、3个 D、4个
8、下列函数中,图象经过原点的为( )
A.y=5x+1 B.y=-5x-1
C.y=- D.y=
[B组]
9、点(a,6),在函数y=的图象上,则a=
10、数y=kx+5的图象经过(1,-2),则k=
[C组]
11、别在同一坐标系内画出各组函数的图象,并观察每组图象之间的关系和区别.
(1)
12、知函数
(1)画出这个函数的图象;
(2)写出相应的函数与x轴交点坐标,与y轴的交点坐标;
(3)判断点 是否在这个函数的图象上,如果在将它画在图象上.
13、若点 在函数 的图象上,且当 时, .
(1)求a、c的值;
(2)如果点(-1,m)和点(n ,6)也在函数的图象上,求m ,n的值.
第三课时
1、一天,亮亮发烧了,早晨他烧得很厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜,亮亮才感觉身上不那么发烫了,下面各图能基本上反映出亮亮这一天(0时-24时)体温的变化情况的是( )
2、星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离与散步的时间t(分)之间的函数关系,依据图象,下面描述符合小红散步情景的是( )
A从家出发,到一个公共阅报栏看了一
会儿报,就回家了。
B从家出发,到一个公共阅报栏看了一
会儿报,继续向前走了一段,然后回家了。
C 从家出发,一直散步(没有停留),然
后回家了。
D从家出发,散了一会儿步,就找同学去
了,18分钟后才开始返回。
3、如果A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
A A比B先出发 B A、B两人的速度相同
C A先到达终点 D B比A跑的路程多
4、丹家距学校m千米,一天她从家上学先以a千米/时的速度跑步锻炼前进,后以匀速b千米/时步行到达学校,共用n小时图17-2-12份中能够反映李丹同学距学校的距离s(千米)与上学的时间t(小时)之间的大致图象是 ( )
5、汽车在行驶过程中,速度往往是变化的,下图图象表示的是一辆汽车的速度随时间变化而变化的情况。
(1) 汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2) 汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3) 出发后8分钟到10分钟辶间可能发生了什么情况?
6、如图,图中直线AB、CD分别表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港的过程中,路程(km)随时间(小时)变化的图象(其中,轮船出发的时间记作0).
(1)分别求出轮船和快艇行驶过程中与间的函数关系式;
(2)求轮船和快艇行驶时的速度分别是多少;
(3)由图中哪点可以得知,快艇出发多少时间赶上轮船,
为什么?
(4)若用函数关系式来解决问题(3),你会怎样做?
为什么?
(4) 结合以上问题和你对图示中点A、B、C、D、E的理解,用一段话描述一下事情的经过.
7、如图表示某学校秋游活动时,学生乘坐旅游车所行走的路程与时间的关系的示意图,请根据示意田回答下列问题:
1.学生何时下车参观第一风景区 参观时间有多长
2.11:00时该车离开学校有多远
3.学生何时返回学校,返回学校时车的平均速度是多少
[B组]
8、小刚,爸爸,爷爷同时从家中出发到达同一目的地后又立即返回,小刚去时骑自行车,返回时步行;爷爷去时步行,返回时骑自行车;爸爸往返都步行。三人步行的速度不等,小刚与爷爷骑自行车的速度相等,每个人走的路程与时间的关系分别如下图中的一个,走完一个往返,小刚用 min,爸爸用 min,爷爷用 min。
9、小明为了表示爷爷吃过晚饭后,出门散步、报亭看报、回家的过程,绘制了爷爷离家的路程S(米)与外出的时间(分)之间的关系图(如图17-1-3所示),请根据这个关系图回答下列问题.
(1) 这个关系图反映了哪几个变量之间的关系?
(2) 任取变量t的一个值,变量S有几个值与它对应,变S是t的函数吗?
(3) 报亭离爷爷家多远?爷爷在报亭看了多长时间的报?
(4) 爷爷出门、返回的平均速度分别是多少?
10、在下列几个图象下的括号内分别填上对应函数的序号:(1)一杯越晾越凉的水(水温与时间的关系)(2)一面冉冉上升的旗子(高度与时间的关系)(3)足球守门员大脚开出去的球(高度与时间的关系)(4)匀速行驶的汽车(速度与时间的关系)
[C组]
11、如图所示是某蓄水池的横断面示意图,分深水区
和浅水区,如果这个蓄水池以固定的流量注水,下
面哪个图象能大致表示水的最大深度h与注水时间t
间的函数关系( )
12、沿墙用长32米的竹篱笆围成一个矩形的护栏(三面),设矩形的宽为x m,求矩形的面积s与x的函数关系式,画出此函数的图象,并指出当x为何值时面积最大?最大面积是多少?
13、一函数的图象如下图,根据图象:观察下图回答下列问题:
(1)确定自变量x的取值范围;
(2)求当 时,y的值;
(3)求当 时,对应的x的值;
(4)当x为何值时,函数值y最大?
(5)当x为何值时,函数值y最小?
(6)当y随x的增大而增大时,求相应的x值在什么范围内?
(7)当y随x的增大而减小时,求相应的x值在什么范围内?
PAGE
1
