3.1.1无理数[上学期]
图片预览




文档简介
课件17张PPT。(一)复习引入
1、什么叫有理数?⑵你会将它们化成小数形式吗?由此,你能得出什么结论? 任何一个有理数都可以化为有限小数或无限循环小数。 有限小数或无限循环小数都是有理数。 综上所述,有理数可用以下两种观点解释:
①整数、分数统称为有理数。
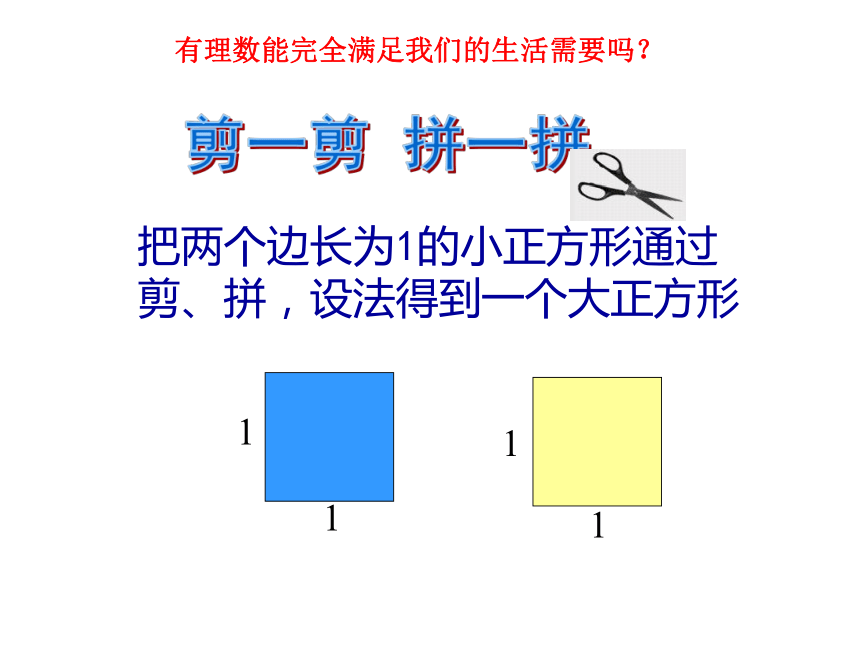
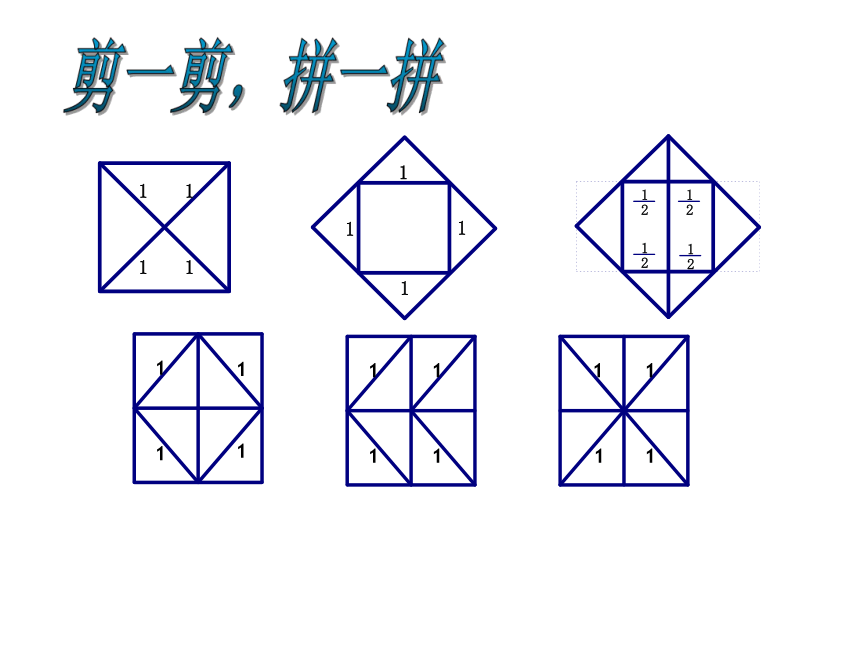
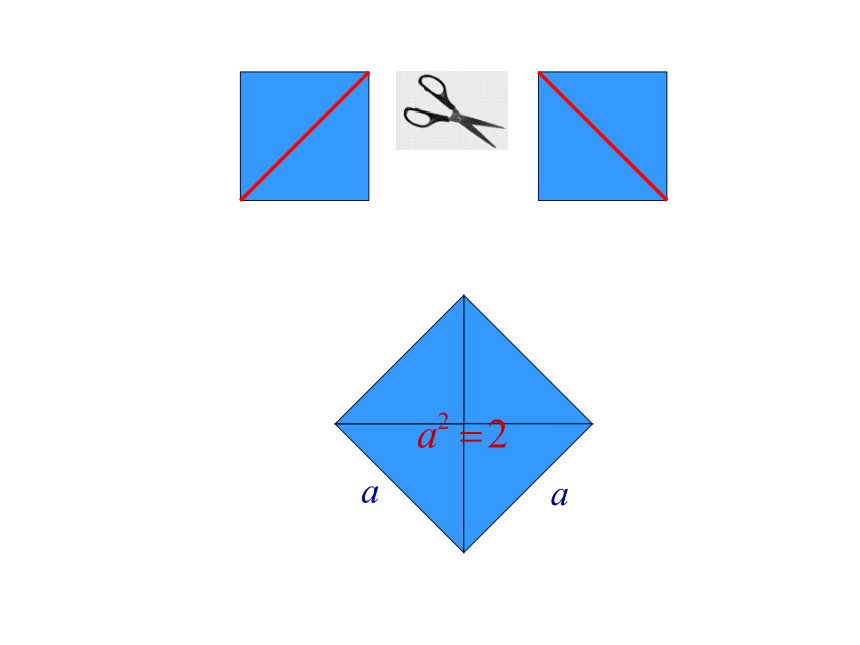
②有限小数或无限循环小数是有理数。把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形剪一剪 拼一拼1111有理数能完全满足我们的生活需要吗?剪一剪,拼一拼议一议111探索:11它是一个无限不循环小数 然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
??? 毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。 但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
做一做b是有理数吗?它是一个无限不循环小数随堂练习1.如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?2.长宽分别是3,2的长方形,它的对 角线的长可能是整数吗?可能是分 数吗?试一试 右图是由16个边长为1的小正方形拼成的,试从连接这些小正方形的两个顶点所得到的线段中,分别找出长度是有理数的线段和长度不是有理数的线段.线段AB,AD,AE的长都能用有理数表示,而线段AC,CE,BE的
长都不能用有理数表示。毕达哥拉斯树螺形图欣赏有趣的图形:小结:谈谈你这节课的收获
1、什么叫有理数?⑵你会将它们化成小数形式吗?由此,你能得出什么结论? 任何一个有理数都可以化为有限小数或无限循环小数。 有限小数或无限循环小数都是有理数。 综上所述,有理数可用以下两种观点解释:
①整数、分数统称为有理数。
②有限小数或无限循环小数是有理数。把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形剪一剪 拼一拼1111有理数能完全满足我们的生活需要吗?剪一剪,拼一拼议一议111探索:11它是一个无限不循环小数 然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
??? 毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。 但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
做一做b是有理数吗?它是一个无限不循环小数随堂练习1.如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?2.长宽分别是3,2的长方形,它的对 角线的长可能是整数吗?可能是分 数吗?试一试 右图是由16个边长为1的小正方形拼成的,试从连接这些小正方形的两个顶点所得到的线段中,分别找出长度是有理数的线段和长度不是有理数的线段.线段AB,AD,AE的长都能用有理数表示,而线段AC,CE,BE的
长都不能用有理数表示。毕达哥拉斯树螺形图欣赏有趣的图形:小结:谈谈你这节课的收获
