贵州省沿河县第一教育集团2022-2023学年九年级下学期第一次学业自查数学试卷(无答案)
文档属性
| 名称 | 贵州省沿河县第一教育集团2022-2023学年九年级下学期第一次学业自查数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 10:57:27 | ||
图片预览

文档简介
沿河第一教育集团2022--2023学年度第二学期第一次学业自查
九年级数学试题
(考试时间:120分钟 试卷满分:150分 命题人:)
一、选择题(本大题共10小题,每题3分,共36分)
1.下列四个数中,最小的数是( )
A.0 B. C.1 D.
2.如图所示的几何体是由4个完全相同的小正方体搭成的,它的主视图是( )
(
B.
C.
D.
)
3.位于我县境内的沙沱水电站,属“西电东送”第二批开工项目的“4水工程”之一。年平均发电量45.89亿kW.h。
数“45.89亿”用科学计数法表示为( )
A. B. C. D.
4.如图,直线c与直线a、b都相交.若,,则( )
A.125° B. C.115° D.
(
第
4题图
第
6题图
第
8题图
第
9题图
第
11题图
)
5.在函数中,自变量的取值范围是( )
A. B. C. D.
6.如图,在中,,则的值是( )
A. B. C. D.
7.两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )
A.两个小球的标号之和等于1 B.两个小球的标号之和等于6
C.两个小球的标号之和大于1 D.两个小球的标号之和大于6
8.我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形的面积是100,小正方形的面积是4,那么( )
A. B. C. D.
9.如图,线段是半圆O的直径,分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线,交半圆O于点C,交于点E,连接,,若,则的长是( )
A. B.4 C.6 D.
10.小红在班上做节水意识调查,收集了班上7位同学家里上个月的用水量(单位:吨)如下:5,5,6,7,8,9,10.她发现,若去掉其中两个数据后,这组数据的中位数、众数保持不变,则去掉的两个数可能是( )
A. 5,10 B. 5,9 C. 6,8 D. 7,8
(
第
12题图
)11.蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
A. 圆柱底面积为4πm2 B. 圆柱的侧面积为10πm2
C. 圆锥的母线AB长为2.25m D. 圆锥的侧面积为5πm2
12.如图,二次函数的图象与y轴的交点在(0,1)与(0,2)
之间,对称轴为,函数最大值为4,结合图象给出下列结论:
①abc > 0; ②; ③;
④若关于x的一元二次方程 有两个不相等的实数根,则m>4;
⑤当x<0时,y随x的增大而减小.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每题4分,共16分)
13.因式分解:=_____.
14.若点都在反比例函数的图象上,则的大小关系是 .
15.小明参加“建团百年,我为团旗添光彩”主题演进比赛,其演讲形象、内容、效果三项得分分别是9分,8分,8分.若将三项得分依次按3∶4∶3的比例确定最终成绩,则小明的最终比赛成绩为__________分.
(
第
16题图
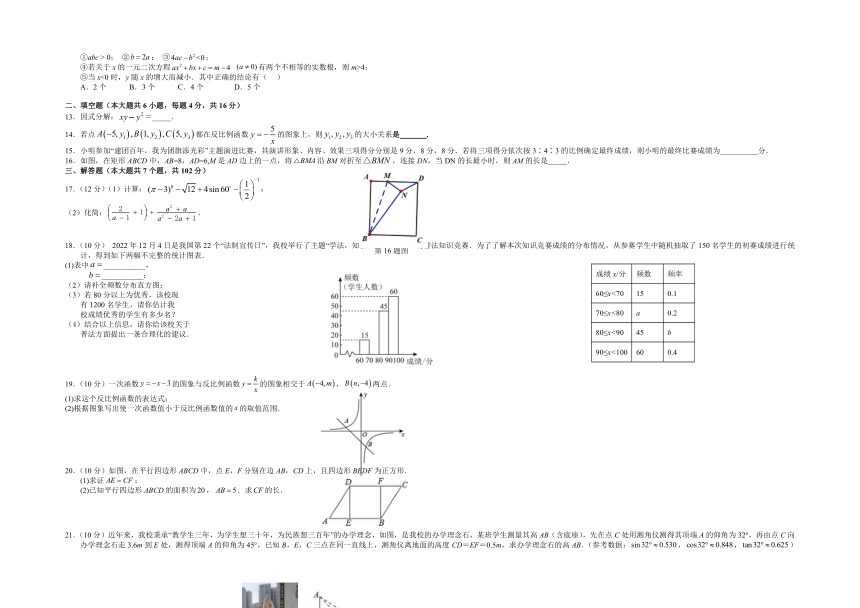
)16.如图,在矩形ABCD中,AB=8,AD=6,M是AD边上的一点,将沿BM对折至,连接DN,当DN的长最小时,则AM的长是_____.
三、解答题(本大题共7个题,共102分)
17.(12分)(1)计算:;
(2)化简:.
18.(10分) 2022年12月4日是我国第22个“法制宣传日”,我校举行了主题“学法,知法,懂法,守法”的普法知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 频率
60≤x<70 15 0.1
70≤x<80 a 0.2
80≤x<90 45 b
90≤x<100 60 0.4
(1)表中___________,
___________;
(2)请补全频数分布直方图:
(3)若80分以上为优秀,该校现
有1200名学生,请你估计我
校成绩优秀的学生有多少名?
结合以上信息,请你给该校关于
普法方面提出一条合理化的建议.
19.(10分)一次函数的图象与反比例函数的图象相交于,两点.
(1)求这个反比例函数的表达式;
(2)根据图象写出使一次函数值小于反比例函数值的的取值范围.
20.(10分)如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证;
(2)已知平行四边形ABCD的面积为,.求的长.
21.(10分)近年来,我校秉承“教学生三年,为学生想三十年,为民族想三百年”的办学理念,如图,是我校的办学理念石,某班学生测量其高AB(含底座),先在点C处用测角仪测得其顶端A的仰角为32°,再由点C向办学理念石走3.6m到E处,测得顶端A的仰角为45°,已知B,E,C三点在同一直线上,测角仪离地面的高度CD=EF=0.5m,求办学理念石的高AB.(参考数据:,,)
22.(10分)冰墩墩(Bing Dwen Dwen)、雪容融(Shuey Rhon Rhon)分别是2022年北京冬奥会、冬残奥会的吉样物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶,决定从该网店进货并销售,第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,每个雪容融玩偶可获利20元.
(1)求两种玩偶的进货价分别是多少?
(2)第二次小雅进货时,网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?
23.(10分)如图,AB为圆的直径, C是⊙O上一点,过点C的直线交AB的延长线于点M.作AD⊥MC,垂足为D,已知AC平分∠MAD .
(1)求证:MC是⊙O的切线:
(2)若 AB=BM=4,求 tan∠MAC的值
24.(12分)小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距
离3m,身高1.6m的小红在水柱下方走动,当
她的头顶恰好接触到水柱时,求她与爸爸的
水平距离.
(
图
①
图
②
图
③
图
④
图
⑤
)25.(14分) 同学们还记得吗?图①是我们研究过的湘教版八年级上册教材P99第16题“已知,如图在等腰三角形ABC中,∠C=90°,D是AB的中点,DE⊥DF 点E、F分别在AC、AB上求证:DE=DF”的图形;图②是我们研究过的湘教版九年级上册教材P90第2题“如图,AB⊥BD,ED⊥BD,C是BD的中点.已知ED=1,BD=4,求AB的长.”的图形,受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】受图①启发,兴趣小组画出了图③,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图④:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图⑤:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
九年级数学试题
(考试时间:120分钟 试卷满分:150分 命题人:)
一、选择题(本大题共10小题,每题3分,共36分)
1.下列四个数中,最小的数是( )
A.0 B. C.1 D.
2.如图所示的几何体是由4个完全相同的小正方体搭成的,它的主视图是( )
(
B.
C.
D.
)
3.位于我县境内的沙沱水电站,属“西电东送”第二批开工项目的“4水工程”之一。年平均发电量45.89亿kW.h。
数“45.89亿”用科学计数法表示为( )
A. B. C. D.
4.如图,直线c与直线a、b都相交.若,,则( )
A.125° B. C.115° D.
(
第
4题图
第
6题图
第
8题图
第
9题图
第
11题图
)
5.在函数中,自变量的取值范围是( )
A. B. C. D.
6.如图,在中,,则的值是( )
A. B. C. D.
7.两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )
A.两个小球的标号之和等于1 B.两个小球的标号之和等于6
C.两个小球的标号之和大于1 D.两个小球的标号之和大于6
8.我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形的面积是100,小正方形的面积是4,那么( )
A. B. C. D.
9.如图,线段是半圆O的直径,分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线,交半圆O于点C,交于点E,连接,,若,则的长是( )
A. B.4 C.6 D.
10.小红在班上做节水意识调查,收集了班上7位同学家里上个月的用水量(单位:吨)如下:5,5,6,7,8,9,10.她发现,若去掉其中两个数据后,这组数据的中位数、众数保持不变,则去掉的两个数可能是( )
A. 5,10 B. 5,9 C. 6,8 D. 7,8
(
第
12题图
)11.蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
A. 圆柱底面积为4πm2 B. 圆柱的侧面积为10πm2
C. 圆锥的母线AB长为2.25m D. 圆锥的侧面积为5πm2
12.如图,二次函数的图象与y轴的交点在(0,1)与(0,2)
之间,对称轴为,函数最大值为4,结合图象给出下列结论:
①abc > 0; ②; ③;
④若关于x的一元二次方程 有两个不相等的实数根,则m>4;
⑤当x<0时,y随x的增大而减小.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每题4分,共16分)
13.因式分解:=_____.
14.若点都在反比例函数的图象上,则的大小关系是 .
15.小明参加“建团百年,我为团旗添光彩”主题演进比赛,其演讲形象、内容、效果三项得分分别是9分,8分,8分.若将三项得分依次按3∶4∶3的比例确定最终成绩,则小明的最终比赛成绩为__________分.
(
第
16题图
)16.如图,在矩形ABCD中,AB=8,AD=6,M是AD边上的一点,将沿BM对折至,连接DN,当DN的长最小时,则AM的长是_____.
三、解答题(本大题共7个题,共102分)
17.(12分)(1)计算:;
(2)化简:.
18.(10分) 2022年12月4日是我国第22个“法制宣传日”,我校举行了主题“学法,知法,懂法,守法”的普法知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 频率
60≤x<70 15 0.1
70≤x<80 a 0.2
80≤x<90 45 b
90≤x<100 60 0.4
(1)表中___________,
___________;
(2)请补全频数分布直方图:
(3)若80分以上为优秀,该校现
有1200名学生,请你估计我
校成绩优秀的学生有多少名?
结合以上信息,请你给该校关于
普法方面提出一条合理化的建议.
19.(10分)一次函数的图象与反比例函数的图象相交于,两点.
(1)求这个反比例函数的表达式;
(2)根据图象写出使一次函数值小于反比例函数值的的取值范围.
20.(10分)如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证;
(2)已知平行四边形ABCD的面积为,.求的长.
21.(10分)近年来,我校秉承“教学生三年,为学生想三十年,为民族想三百年”的办学理念,如图,是我校的办学理念石,某班学生测量其高AB(含底座),先在点C处用测角仪测得其顶端A的仰角为32°,再由点C向办学理念石走3.6m到E处,测得顶端A的仰角为45°,已知B,E,C三点在同一直线上,测角仪离地面的高度CD=EF=0.5m,求办学理念石的高AB.(参考数据:,,)
22.(10分)冰墩墩(Bing Dwen Dwen)、雪容融(Shuey Rhon Rhon)分别是2022年北京冬奥会、冬残奥会的吉样物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶,决定从该网店进货并销售,第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,每个雪容融玩偶可获利20元.
(1)求两种玩偶的进货价分别是多少?
(2)第二次小雅进货时,网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?
23.(10分)如图,AB为圆的直径, C是⊙O上一点,过点C的直线交AB的延长线于点M.作AD⊥MC,垂足为D,已知AC平分∠MAD .
(1)求证:MC是⊙O的切线:
(2)若 AB=BM=4,求 tan∠MAC的值
24.(12分)小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距
离3m,身高1.6m的小红在水柱下方走动,当
她的头顶恰好接触到水柱时,求她与爸爸的
水平距离.
(
图
①
图
②
图
③
图
④
图
⑤
)25.(14分) 同学们还记得吗?图①是我们研究过的湘教版八年级上册教材P99第16题“已知,如图在等腰三角形ABC中,∠C=90°,D是AB的中点,DE⊥DF 点E、F分别在AC、AB上求证:DE=DF”的图形;图②是我们研究过的湘教版九年级上册教材P90第2题“如图,AB⊥BD,ED⊥BD,C是BD的中点.已知ED=1,BD=4,求AB的长.”的图形,受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】受图①启发,兴趣小组画出了图③,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图④:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图⑤:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
同课章节目录
