沪科版 八年级数学下册试题 17.5一元二次方程的应用-(含答案)
文档属性
| 名称 | 沪科版 八年级数学下册试题 17.5一元二次方程的应用-(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 908.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 15:48:24 | ||
图片预览



文档简介
17.5一元二次方程的应用
一、解答题
1.一家水果店以每斤3元的价格购进“官地洼”甜瓜若干斤,然后以每斤5元的价格出售,每天可售出100斤,通过调查发现,这种甜瓜每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将“官地洼”甜瓜每斤的售价降低元,则每天的销售量是多少斤(用含的代数式表示);
(2)销售这批“官地洼”甜瓜要想每天盈利300元,且保证每天至少售出280斤,那么水果店需将每斤的售价降低多少元?
2.某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件,设每件衣服降价元.
(1)现在每天卖出 件,每件盈利 元(用含的代数式表示);
(2)求当为何值时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠;
(3)要想平均每天盈利2000元,可能吗?请说明理由.
3.新冠病毒肆虐全球,在以习近平为核心的党中央的英明领导下,我国的疫情很快得到了控制,并且研发出安全性有效性均非常高的疫苗.今年七月,国家发布通知,岁未成年人也可接种新冠疫苗,海航医院为某镇定点疫苗接种医院,第一批未成年人接种疫苗时间定为8月1日至8月3日.
(1)已知在海航医院投放第一批“智飞”和“科兴”两种疫苗共1800支,两种疫苗每天按定量接种.其中,“智飞”疫苗可供接种3天;“科兴”疫苗可供接种2天,“智飞”疫苗每天接种比“科兴”多100支,则海航医院每天接种“智飞”和“科兴”疫苗各多少支?
(2)疫情情况直接影响各企业生产与销售情况,某镇某家具厂有甲、乙两个车间,甲车间生产一种实木椅子,乙车间生产一种实木床.今年6月,该厂生产的椅子数量为床的数量的20倍,椅子售价为每把75元,床售价为每个1000元.今年7月,椅子的生产数量比6月少,床的生产数量比6月少.在售卖这批产品时,椅子价格不变,床的价格比6月增加.全部售完后,发现7月生产的产品销售额比6月生产的产品销售额少,求的值.
4.返校复学之际,育才学校为每个班级准备了免洗抑菌洗手液.去市场购买时发现当购买量不超过100瓶时,免洗抑菌洗手液的单价为8元;超过100瓶时,每增加10瓶,每瓶单价就降低0.2元,但最低价格不能低于每瓶5元,设学校共买了瓶免洗抑菌洗手液.
(1)当时,每瓶洗手液的价格是 元;当时,每瓶洗手液的价格是 元;当时,每瓶洗手液的价格为 元(用含的式子表示);
(2)若学校一次性购买洗手液共花费1200元,问一共购买了多少瓶洗手液?
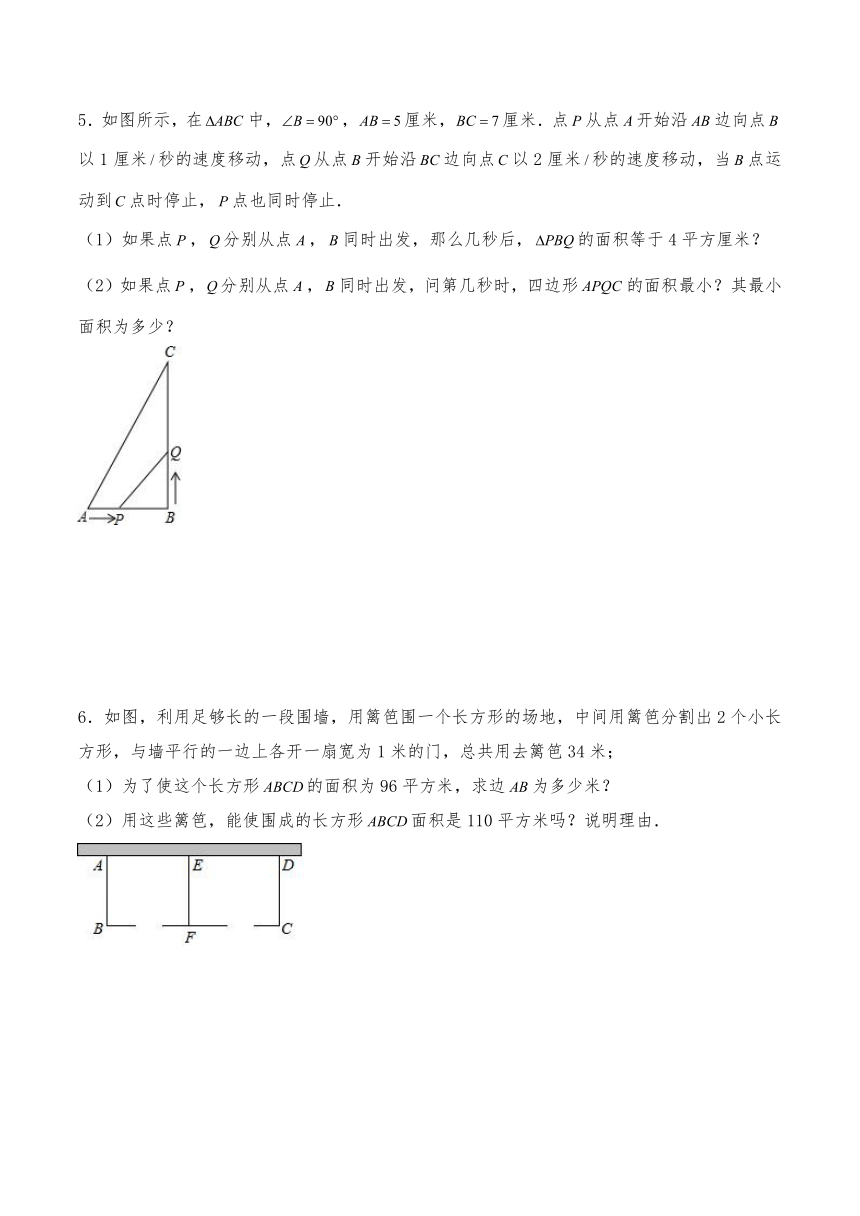
5.如图所示,在中,,厘米,厘米.点从点开始沿边向点以1厘米秒的速度移动,点从点开始沿边向点以2厘米秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于4平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
6.如图,利用足够长的一段围墙,用篱笆围一个长方形的场地,中间用篱笆分割出2个小长方形,与墙平行的一边上各开一扇宽为1米的门,总共用去篱笆34米;
(1)为了使这个长方形的面积为96平方米,求边为多少米?
(2)用这些篱笆,能使围成的长方形面积是110平方米吗?说明理由.
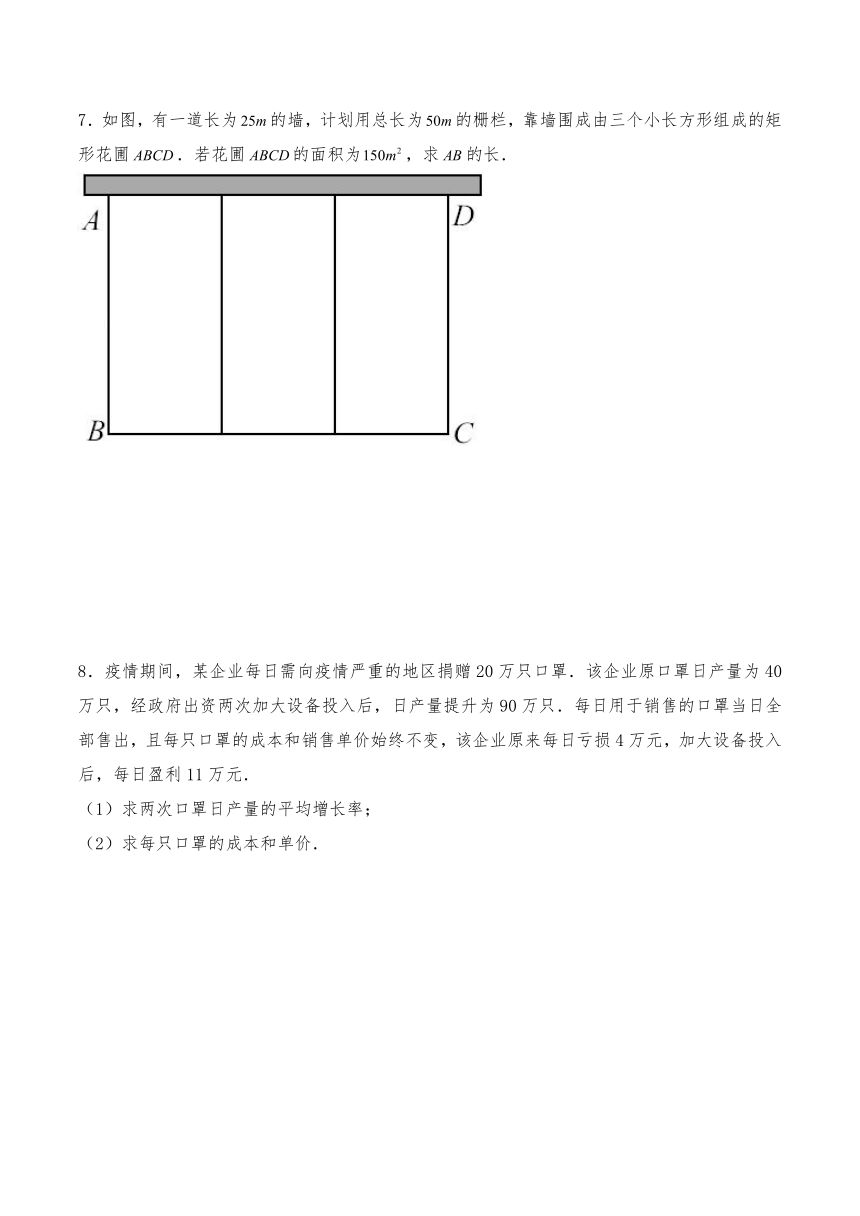
7.如图,有一道长为的墙,计划用总长为的栅栏,靠墙围成由三个小长方形组成的矩形花圃.若花圃的面积为,求的长.
8.疫情期间,某企业每日需向疫情严重的地区捐赠20万只口罩.该企业原口罩日产量为40万只,经政府出资两次加大设备投入后,日产量提升为90万只.每日用于销售的口罩当日全部售出,且每只口罩的成本和销售单价始终不变,该企业原来每日亏损4万元,加大设备投入后,每日盈利11万元.
(1)求两次口罩日产量的平均增长率;
(2)求每只口罩的成本和单价.
9.为响应国家“垃圾分类”的号召,温州市开始实施《城镇垃圾分类标准》,某商场向厂家订购了,两款垃圾桶共100个,已知购买款垃圾桶个数不超过30个时,每个款垃圾桶进价为80元,若超过30个时,每增加1个垃圾桶,则该款垃圾桶每个进价减少2元,厂家为保障盈利,每个款垃圾桶进价不低于50元.每个款垃圾桶的进价为40元,设所购买款垃圾桶的个数为个.
(1)根据信息填表:
款式 数量(个 进价(元个)
(不超过30个时) 80
(超过30个时)
40
(2)若订购的垃圾桶的总进价为4800元,则该商场订购了多少个款垃圾桶?
10.随着宁波轨道交通4号线的开通,充满魅力的千年古城慈城,吸引了越来越多的游客前来.说到慈城,不得不提软糯香甜的年糕,《舌尖上的中国》专门介绍了宁波的这一特色美食.慈城某商店于今年三月初以每件40元的进价购进一批水磨年糕,当年糕售价为每件60元时,三月份共销售192件.四、五月该批年糕销售量持续走高,在售价不变的基础上,五月份的销售量达到300件.
(1)求四、五两个月销售量的月平均增长率;
(2)从六月份起,在五月份的基础上,商店决定采用降价促销的方式回馈顾客,经市场调查发现,该年糕每件降价1元,月销售量增加20件.在顾客获得最大实惠的前提下,当年糕每件降价多少元时,商场六月仍可获利为6080元?
11.圆圆想买一个蓝牙耳机,家边上数码城售卖的某款蓝牙耳机,原来每只售价400元,经过连续两次降价后,现在每只售价256元.
(1)求平均每次降价的百分率;
(2)某电商平台“618”搞活动,同款蓝牙耳机原价是300元,现在7折优惠,包邮到家.同时,数码城按照前两次的平均降价率进行第三次降价.请问:圆圆选择哪种方式购买比较合算?请通过计算说明.
12.某商品进价为每件40元,现售价为每件60元,每星期可卖出300件,经市场调查反映,每次涨价1元,每星期可少卖10件.
(1)在一个星期内要想获利6090元的利润,尽量减少库存,该商品应涨价多少元;
(2)在一个星期内能否获利7000元,若能,请求出商品的定价,若不能,请说明理由.
13.某租赁公司有房屋100套.据统计,当每套房屋的月租金为3000元时,可全部租出.每套房屋的月租金每增加50元,租出的房屋数将减少1套.
(1)当每套房屋的月租金定为3500元时,能租出多少套?
(2)当每套房屋的月租金定价为多少元时,租赁公司的月租金可达到315000元?
14.随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆120元.据统计,三月份的全天包车数为25次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到64次.
(1)若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;
(2)从六月份起,该公司决定降低租金,经调查发现,租金每降价元,全天包车数增加次,当租金降价多少元时,公司将获利8800元?
15.新华商场销售某种商品,每件进货价为40元,市场调研表明:当销售价为80元时,平均每天能售出20件;在每件盈利不少于25元的前提下,经过一段时间销售,当销售价每降低1元时,平均每天就能多售出2件.
(1)若降价2元,则平均每天销售数量为 件;
(2)当每件商品定价多少元时,该商场平均每天销售某种商品利润达到1200元?
16.如图,点P是边长为6cm的正方形ABCD内部一点,过点P分别作AB,AD的平行线,将正方形分成一、二、三、四共四个不重合的部分,其中第一部分是边长小于3cm的正方形.当第一、四部分的面积和是第二、三部分面积和的3倍时,求第一部分的边长.
17.某商店以每件40元的价格进了一批热销商品,出售价格经过两个月的调整,从每件50元上涨到每件72元,此时每月可售出188件商品.
(1)求该商品平均每月的价格增长率;
(2)因某些原因,商家需尽快将这批商品售出,决定降价出售.经过市场调查发现:售价每下降一元,每个月多卖出一件,设实际售价为元,则为多少元时商品每月的利润可达到4000元.
18.列方程(组解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
19.某工艺厂设计了一款成本为10元件的工艺品投放市场进行试销.经过调查,每天销售量件)与销售单价(元件)满足一次函数关系,其部分对应数据如表.
销售单价(元件) 20 30 40
每天销售量件) 500 400 300
(1)把表中、的各组对应值作为点的坐标,求出函数关系式;
(2)相关物价部门规定,该工艺品销售单价最高不能超过35元件,当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?
20.为促进新旧功能转换,提高经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为25万元,经过市场调研发现,该设备的月销售量(台和销售单价(万元)满足如图所示的一次函数关系.
(1)求月销售量与销售单价的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于35万元,如果该公司想获得130万元的月利润,那么该设备的销售单价应是多少万元?
21.如图,某校准备一面利用墙,其余三面用篱笆围成一个矩形花圃.已知旧墙可利用的最大长度为,篱笆长为,设垂直于墙的边长为.
(1)若围成的花圃面积为时,求的长;
(2)如图,若计划将花圃中间用一道篱笆隔成两个小矩形,且花圃面积为,请你判断能否围成这样的花圃?如果能,求的长;如果不能,请说明理由.
22.因粤港澳大湾区和中国特色社会主义先行示范区的双重利好,深圳已成为国内外游客最喜欢的旅游目的地城市之一,深圳著名旅游“网红打卡地”东部华侨城景区在2019年春节长假期间,共接待游客达20万人次,预计在2021年春节长假期间,将接待游客达28.8万人次.
(1)求东部华侨城景区2019至2021年春节长假期间接待游客人次的平均增长率.
(2)东部华侨城景区一奶茶店销售一款奶茶,每杯成本价为6元,根据销售经验,在旅游旺季,若每杯定价25元,则平均每天可销售300杯,若每杯价格降低1元,则平均每天可多销售30杯,2021年春节期间,店家决定进行降价促销活动,则当每杯售价定为多少元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额?
23.某农场要建一个饲养场(矩形,两面靠墙位置的墙最大可用长度为27米,位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.
(1)若饲养场(矩形的一边长为8米,则另一边 米.
(2)若饲养场(矩形的面积为180平方米,求边的长.
(3)饲养场的面积能达到210平方米吗?若能达到,求出边的长;若不能达到,请说明理由.
24.在“精准扶贫”工作中,某单位建议贫困户借助家里长的墙建造面积为的长方形区域来养一些家禽,该单位给贫困户提供长的篱笆(全部用于建造长方形区域),并提供如图所示的两种方案:
(1)如图1,若选取墙的一部分作为长方形的一边,其他三边用篱笆围成,则在墙上借用的的长度为多少?
(2)如图2,若将墙全部借用,并在墙的延长线上拓展,构成长方形,,,和都由篱笆构成,求的长.
答案
一、解答题
1.(1)(斤.
答:每天的销售量是斤.
(2)依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
.
答:水果店需将每斤的售价降低1元.
2.(1)由题意得:每天卖出衣服的数量为:件,
每件的盈利为:元,
故答案为:,;
(2)由题意得:
,
解得:,,
为使顾客得到较多的实惠,应取;
(3)不可能,理由如下:
依题意得:
,
整理得:,
△,
则原方程无实数解.
则不可能每天盈利2000元.
3.(1)设海航医院每天接种“智飞”疫苗支,每天接种“科兴”疫苗支,
依题意得:,
解得:.
答:海航医院每天接种“智飞”疫苗400支,每天接种“科兴”疫苗300支.
(2)设今年6月该厂生产实木床个,则生产椅子把,
依题意得:,
整理得:,
解得:,(不合题意,舍去).
答:的值为10.
4.(1)当时,每瓶洗手液的价格是8元;当时,每瓶洗手液的价格是(元;当时,每瓶洗手液的价格为(元,当时,每瓶洗手液的价格是5元.
故答案为:8;7;.
(2)(元(元,
.
当时,,
整理得:,
解得:,(不合题意,舍去);
当时,,
解得:(不合题意,舍去).
答:一共购买了200瓶洗手液.
5.(1)设秒钟后,的面积等于,由题意可得:
.
解得,.
经检验均是原方程的解.
答:故经过1或4秒钟时,的面积等于.
(2)依题意有:
,
故经过秒时,四边形的面积最小,最小值是.
6.(1)设的长为米,
依题意的方程:,
解得:,,
答:当的长度为4米或8米时,长方形的面积为96平方米;
(2)不能.
理由:”假设长方形的面积是110平方米,
依题意得:.即,
△,
该一元二次方程无实数根,
假设不成立,
长方形的面积是不能为110平方米.
7.设,则,
依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
答:的长为.
8.(1)设两次口罩日产量的平均增长率为,
依题意得:,
解得:,(不合题意,舍去).
答:两次口罩日产量的平均增长率为.
(2)设每只口罩的成本为元,单价为元,
依题意得:,
解得:.
答:每只口罩的成本为0.5元,单价为0.8元.
9.(1)(个.
当时,款垃圾桶的进价为(元个);
当时,款垃圾桶的进价为50元个.
,两款垃圾桶共购进100个,款垃圾桶购进个,
款垃圾桶购进个.
故答案为:;.
(2)当时,,
解得:;
当时,,
化简得:,
解得:,(不合题意,舍去);
当时,,
解得:.
答:该商场订购了20个或40个或80个款垃圾桶.
10.(1)设四、五两个月销售量的月平均增长率为,
由题意,得:,
解得:,(不合题意,舍去),
四、五两个月销售量的月平均增长率为;
(2)设年糕每件降价元时,商场六月仍可获利为6080元,
由题意,得:,
化简,得:,
解得:或,
顾客获得最大实惠的前提下,,
在顾客获得最大实惠的前提下,当年糕每件降价4元时,商场六月仍可获利为6080元.
11.(1)设平均每次降价的百分率为,
依题意得:,
解得:,(不合题意,舍去).
答:平均每次降价的百分率为.
(2)选择在数码城购买比较合算,理由如下:
在电商平台购买所需费用为(元,
在数码城购买所需费用为(元.
,
选择在数码城购买比较合算.
12.(1)设每件涨价元,则每件的利润为元,每星期可售出件,
依题意得:,
整理得:,
解得:,.
尽量减少库存,
.
答:该商品应涨价1元.
(2)设每件涨价元,则每件的利润为元,每星期可售出件,
依题意得:,
整理得:,
△,
此方程没有实数根,
不能获利7000元.
13.(1)(套.
答:当每套房屋的月租金定为3500元时,能租出90套.
(2)设每套房屋的月租金定价为元,则可租出套房屋,
依题意得:,
整理得:,
解得:,.
答:当每套房屋的月租金定价为4500元或3500元时,租赁公司的月租金可达到315000元.
14.(1)设全天包车数的月平均增长率为,
根据题意可得:,
解得:,(不合题意舍去),
答:全天包车数的月平均增长率为;
(2)根据题意可得:,
化简得:,
解得:,.
答:当租金降价10元或70元时,公司将获利8800元.
15.(1)(件.
故答案为:24.
(2)设每件商品降价元,则平均每天可销售件,
依题意,得:,
整理,得:,
解得:,.
当时,,
舍去.
定价(元
答:当每件商品定价70元时,该商店每天销售利润为1200元.
16.设第一部分的边长为x(0<x<3)cm,则第四部分的边长为(6﹣x)cm,
依题意得:x2+(6﹣x)2=3[x(6﹣x)+x(6﹣x)],
整理得:2x2﹣12x+9=0,
解得:x1=,x2=(不合题意,舍去).
答:第一部分的边长为cm.
17.(1)设该商品平均每月的价格增长率为,
依题意,得:,
解得:,(不合题意,舍去).
答:该商品平均每月的价格增长率为.
(2)依题意,得:,
整理,得:,
解得:,.
商家需尽快将这批商品售出,
.
答:为60元时商品每天的利润可达到4000元.
18.设每千克降低元,超市每天可获得销售利润3640元,由题意得,
,
整理得,
或.
要尽可能让顾客得到实惠,
,
售价为元千克.
答:水果的销售价为每千克29元时,超市每天可获得销售利润3640元.
19.(1)可猜想与是一次函数关系,设这个一次函数为,
这个一次函数的图象经过、这两点,
,
解得,
函数关系式是.
(2)设工艺厂试销该工艺品实际售价为元,
依题意得:,
解得,,(舍,
所以,当售价为30元时,利润为8000元.
20.(1)设与的函数关系式为,
依题意,得解得
所以与的函数关系式为.
(2)依题知.
整理方程,得.
解得,.
此设备的销售单价不得高于35万元,
(舍,所以.
答:该设备的销售单价应是27 万元.
21.(1)解:根据题意得:,
则,
解得:,,
当时,时,,
墙可利用的最大长度为,舍去.
答:的长为.
(2)解:不能围成这样的花圃.理由如下:
依题意可知:,
即,△,
所以方程无实数根,
答:不能围成这样的花圃.
22.(1)设年平均增长率为,由题意得:
,
解得:,(舍去).
答:东部华侨城景区2019至2021年春节长假期间接待游客人次的平均增长率为.
(2)设每杯售价定为元,由题意得:
,
解得:,.
为了能让顾客获得最大优惠,故取20.
答:每杯售价定为20元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额.
23.(1)(米.
故答案为:24.
(2)设米,则米,
依题意得:,
整理得:,
解得:,.
当时,(米,,不合题意,舍去;
当时,(米,符合题意.
答:边的长为10米.
(3)不能,理由如下:
设米,则米,
依题意得:,
整理得:.
△,
该方程没有实数根,
饲养场的面积不能达到210平方米.
24.(1)设的长度为,则,
依题意得:,
解得:,.
墙的长为,
不合题意,舍去,
.
答:在墙上借用的的长度为.
(2)设的长为,则,
依题意得:,
解得:,(不合题意,舍去),
.
答:的长为.
一、解答题
1.一家水果店以每斤3元的价格购进“官地洼”甜瓜若干斤,然后以每斤5元的价格出售,每天可售出100斤,通过调查发现,这种甜瓜每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将“官地洼”甜瓜每斤的售价降低元,则每天的销售量是多少斤(用含的代数式表示);
(2)销售这批“官地洼”甜瓜要想每天盈利300元,且保证每天至少售出280斤,那么水果店需将每斤的售价降低多少元?
2.某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件,设每件衣服降价元.
(1)现在每天卖出 件,每件盈利 元(用含的代数式表示);
(2)求当为何值时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠;
(3)要想平均每天盈利2000元,可能吗?请说明理由.
3.新冠病毒肆虐全球,在以习近平为核心的党中央的英明领导下,我国的疫情很快得到了控制,并且研发出安全性有效性均非常高的疫苗.今年七月,国家发布通知,岁未成年人也可接种新冠疫苗,海航医院为某镇定点疫苗接种医院,第一批未成年人接种疫苗时间定为8月1日至8月3日.
(1)已知在海航医院投放第一批“智飞”和“科兴”两种疫苗共1800支,两种疫苗每天按定量接种.其中,“智飞”疫苗可供接种3天;“科兴”疫苗可供接种2天,“智飞”疫苗每天接种比“科兴”多100支,则海航医院每天接种“智飞”和“科兴”疫苗各多少支?
(2)疫情情况直接影响各企业生产与销售情况,某镇某家具厂有甲、乙两个车间,甲车间生产一种实木椅子,乙车间生产一种实木床.今年6月,该厂生产的椅子数量为床的数量的20倍,椅子售价为每把75元,床售价为每个1000元.今年7月,椅子的生产数量比6月少,床的生产数量比6月少.在售卖这批产品时,椅子价格不变,床的价格比6月增加.全部售完后,发现7月生产的产品销售额比6月生产的产品销售额少,求的值.
4.返校复学之际,育才学校为每个班级准备了免洗抑菌洗手液.去市场购买时发现当购买量不超过100瓶时,免洗抑菌洗手液的单价为8元;超过100瓶时,每增加10瓶,每瓶单价就降低0.2元,但最低价格不能低于每瓶5元,设学校共买了瓶免洗抑菌洗手液.
(1)当时,每瓶洗手液的价格是 元;当时,每瓶洗手液的价格是 元;当时,每瓶洗手液的价格为 元(用含的式子表示);
(2)若学校一次性购买洗手液共花费1200元,问一共购买了多少瓶洗手液?
5.如图所示,在中,,厘米,厘米.点从点开始沿边向点以1厘米秒的速度移动,点从点开始沿边向点以2厘米秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于4平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
6.如图,利用足够长的一段围墙,用篱笆围一个长方形的场地,中间用篱笆分割出2个小长方形,与墙平行的一边上各开一扇宽为1米的门,总共用去篱笆34米;
(1)为了使这个长方形的面积为96平方米,求边为多少米?
(2)用这些篱笆,能使围成的长方形面积是110平方米吗?说明理由.
7.如图,有一道长为的墙,计划用总长为的栅栏,靠墙围成由三个小长方形组成的矩形花圃.若花圃的面积为,求的长.
8.疫情期间,某企业每日需向疫情严重的地区捐赠20万只口罩.该企业原口罩日产量为40万只,经政府出资两次加大设备投入后,日产量提升为90万只.每日用于销售的口罩当日全部售出,且每只口罩的成本和销售单价始终不变,该企业原来每日亏损4万元,加大设备投入后,每日盈利11万元.
(1)求两次口罩日产量的平均增长率;
(2)求每只口罩的成本和单价.
9.为响应国家“垃圾分类”的号召,温州市开始实施《城镇垃圾分类标准》,某商场向厂家订购了,两款垃圾桶共100个,已知购买款垃圾桶个数不超过30个时,每个款垃圾桶进价为80元,若超过30个时,每增加1个垃圾桶,则该款垃圾桶每个进价减少2元,厂家为保障盈利,每个款垃圾桶进价不低于50元.每个款垃圾桶的进价为40元,设所购买款垃圾桶的个数为个.
(1)根据信息填表:
款式 数量(个 进价(元个)
(不超过30个时) 80
(超过30个时)
40
(2)若订购的垃圾桶的总进价为4800元,则该商场订购了多少个款垃圾桶?
10.随着宁波轨道交通4号线的开通,充满魅力的千年古城慈城,吸引了越来越多的游客前来.说到慈城,不得不提软糯香甜的年糕,《舌尖上的中国》专门介绍了宁波的这一特色美食.慈城某商店于今年三月初以每件40元的进价购进一批水磨年糕,当年糕售价为每件60元时,三月份共销售192件.四、五月该批年糕销售量持续走高,在售价不变的基础上,五月份的销售量达到300件.
(1)求四、五两个月销售量的月平均增长率;
(2)从六月份起,在五月份的基础上,商店决定采用降价促销的方式回馈顾客,经市场调查发现,该年糕每件降价1元,月销售量增加20件.在顾客获得最大实惠的前提下,当年糕每件降价多少元时,商场六月仍可获利为6080元?
11.圆圆想买一个蓝牙耳机,家边上数码城售卖的某款蓝牙耳机,原来每只售价400元,经过连续两次降价后,现在每只售价256元.
(1)求平均每次降价的百分率;
(2)某电商平台“618”搞活动,同款蓝牙耳机原价是300元,现在7折优惠,包邮到家.同时,数码城按照前两次的平均降价率进行第三次降价.请问:圆圆选择哪种方式购买比较合算?请通过计算说明.
12.某商品进价为每件40元,现售价为每件60元,每星期可卖出300件,经市场调查反映,每次涨价1元,每星期可少卖10件.
(1)在一个星期内要想获利6090元的利润,尽量减少库存,该商品应涨价多少元;
(2)在一个星期内能否获利7000元,若能,请求出商品的定价,若不能,请说明理由.
13.某租赁公司有房屋100套.据统计,当每套房屋的月租金为3000元时,可全部租出.每套房屋的月租金每增加50元,租出的房屋数将减少1套.
(1)当每套房屋的月租金定为3500元时,能租出多少套?
(2)当每套房屋的月租金定价为多少元时,租赁公司的月租金可达到315000元?
14.随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆120元.据统计,三月份的全天包车数为25次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到64次.
(1)若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;
(2)从六月份起,该公司决定降低租金,经调查发现,租金每降价元,全天包车数增加次,当租金降价多少元时,公司将获利8800元?
15.新华商场销售某种商品,每件进货价为40元,市场调研表明:当销售价为80元时,平均每天能售出20件;在每件盈利不少于25元的前提下,经过一段时间销售,当销售价每降低1元时,平均每天就能多售出2件.
(1)若降价2元,则平均每天销售数量为 件;
(2)当每件商品定价多少元时,该商场平均每天销售某种商品利润达到1200元?
16.如图,点P是边长为6cm的正方形ABCD内部一点,过点P分别作AB,AD的平行线,将正方形分成一、二、三、四共四个不重合的部分,其中第一部分是边长小于3cm的正方形.当第一、四部分的面积和是第二、三部分面积和的3倍时,求第一部分的边长.
17.某商店以每件40元的价格进了一批热销商品,出售价格经过两个月的调整,从每件50元上涨到每件72元,此时每月可售出188件商品.
(1)求该商品平均每月的价格增长率;
(2)因某些原因,商家需尽快将这批商品售出,决定降价出售.经过市场调查发现:售价每下降一元,每个月多卖出一件,设实际售价为元,则为多少元时商品每月的利润可达到4000元.
18.列方程(组解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
19.某工艺厂设计了一款成本为10元件的工艺品投放市场进行试销.经过调查,每天销售量件)与销售单价(元件)满足一次函数关系,其部分对应数据如表.
销售单价(元件) 20 30 40
每天销售量件) 500 400 300
(1)把表中、的各组对应值作为点的坐标,求出函数关系式;
(2)相关物价部门规定,该工艺品销售单价最高不能超过35元件,当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?
20.为促进新旧功能转换,提高经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为25万元,经过市场调研发现,该设备的月销售量(台和销售单价(万元)满足如图所示的一次函数关系.
(1)求月销售量与销售单价的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于35万元,如果该公司想获得130万元的月利润,那么该设备的销售单价应是多少万元?
21.如图,某校准备一面利用墙,其余三面用篱笆围成一个矩形花圃.已知旧墙可利用的最大长度为,篱笆长为,设垂直于墙的边长为.
(1)若围成的花圃面积为时,求的长;
(2)如图,若计划将花圃中间用一道篱笆隔成两个小矩形,且花圃面积为,请你判断能否围成这样的花圃?如果能,求的长;如果不能,请说明理由.
22.因粤港澳大湾区和中国特色社会主义先行示范区的双重利好,深圳已成为国内外游客最喜欢的旅游目的地城市之一,深圳著名旅游“网红打卡地”东部华侨城景区在2019年春节长假期间,共接待游客达20万人次,预计在2021年春节长假期间,将接待游客达28.8万人次.
(1)求东部华侨城景区2019至2021年春节长假期间接待游客人次的平均增长率.
(2)东部华侨城景区一奶茶店销售一款奶茶,每杯成本价为6元,根据销售经验,在旅游旺季,若每杯定价25元,则平均每天可销售300杯,若每杯价格降低1元,则平均每天可多销售30杯,2021年春节期间,店家决定进行降价促销活动,则当每杯售价定为多少元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额?
23.某农场要建一个饲养场(矩形,两面靠墙位置的墙最大可用长度为27米,位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.
(1)若饲养场(矩形的一边长为8米,则另一边 米.
(2)若饲养场(矩形的面积为180平方米,求边的长.
(3)饲养场的面积能达到210平方米吗?若能达到,求出边的长;若不能达到,请说明理由.
24.在“精准扶贫”工作中,某单位建议贫困户借助家里长的墙建造面积为的长方形区域来养一些家禽,该单位给贫困户提供长的篱笆(全部用于建造长方形区域),并提供如图所示的两种方案:
(1)如图1,若选取墙的一部分作为长方形的一边,其他三边用篱笆围成,则在墙上借用的的长度为多少?
(2)如图2,若将墙全部借用,并在墙的延长线上拓展,构成长方形,,,和都由篱笆构成,求的长.
答案
一、解答题
1.(1)(斤.
答:每天的销售量是斤.
(2)依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
.
答:水果店需将每斤的售价降低1元.
2.(1)由题意得:每天卖出衣服的数量为:件,
每件的盈利为:元,
故答案为:,;
(2)由题意得:
,
解得:,,
为使顾客得到较多的实惠,应取;
(3)不可能,理由如下:
依题意得:
,
整理得:,
△,
则原方程无实数解.
则不可能每天盈利2000元.
3.(1)设海航医院每天接种“智飞”疫苗支,每天接种“科兴”疫苗支,
依题意得:,
解得:.
答:海航医院每天接种“智飞”疫苗400支,每天接种“科兴”疫苗300支.
(2)设今年6月该厂生产实木床个,则生产椅子把,
依题意得:,
整理得:,
解得:,(不合题意,舍去).
答:的值为10.
4.(1)当时,每瓶洗手液的价格是8元;当时,每瓶洗手液的价格是(元;当时,每瓶洗手液的价格为(元,当时,每瓶洗手液的价格是5元.
故答案为:8;7;.
(2)(元(元,
.
当时,,
整理得:,
解得:,(不合题意,舍去);
当时,,
解得:(不合题意,舍去).
答:一共购买了200瓶洗手液.
5.(1)设秒钟后,的面积等于,由题意可得:
.
解得,.
经检验均是原方程的解.
答:故经过1或4秒钟时,的面积等于.
(2)依题意有:
,
故经过秒时,四边形的面积最小,最小值是.
6.(1)设的长为米,
依题意的方程:,
解得:,,
答:当的长度为4米或8米时,长方形的面积为96平方米;
(2)不能.
理由:”假设长方形的面积是110平方米,
依题意得:.即,
△,
该一元二次方程无实数根,
假设不成立,
长方形的面积是不能为110平方米.
7.设,则,
依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
答:的长为.
8.(1)设两次口罩日产量的平均增长率为,
依题意得:,
解得:,(不合题意,舍去).
答:两次口罩日产量的平均增长率为.
(2)设每只口罩的成本为元,单价为元,
依题意得:,
解得:.
答:每只口罩的成本为0.5元,单价为0.8元.
9.(1)(个.
当时,款垃圾桶的进价为(元个);
当时,款垃圾桶的进价为50元个.
,两款垃圾桶共购进100个,款垃圾桶购进个,
款垃圾桶购进个.
故答案为:;.
(2)当时,,
解得:;
当时,,
化简得:,
解得:,(不合题意,舍去);
当时,,
解得:.
答:该商场订购了20个或40个或80个款垃圾桶.
10.(1)设四、五两个月销售量的月平均增长率为,
由题意,得:,
解得:,(不合题意,舍去),
四、五两个月销售量的月平均增长率为;
(2)设年糕每件降价元时,商场六月仍可获利为6080元,
由题意,得:,
化简,得:,
解得:或,
顾客获得最大实惠的前提下,,
在顾客获得最大实惠的前提下,当年糕每件降价4元时,商场六月仍可获利为6080元.
11.(1)设平均每次降价的百分率为,
依题意得:,
解得:,(不合题意,舍去).
答:平均每次降价的百分率为.
(2)选择在数码城购买比较合算,理由如下:
在电商平台购买所需费用为(元,
在数码城购买所需费用为(元.
,
选择在数码城购买比较合算.
12.(1)设每件涨价元,则每件的利润为元,每星期可售出件,
依题意得:,
整理得:,
解得:,.
尽量减少库存,
.
答:该商品应涨价1元.
(2)设每件涨价元,则每件的利润为元,每星期可售出件,
依题意得:,
整理得:,
△,
此方程没有实数根,
不能获利7000元.
13.(1)(套.
答:当每套房屋的月租金定为3500元时,能租出90套.
(2)设每套房屋的月租金定价为元,则可租出套房屋,
依题意得:,
整理得:,
解得:,.
答:当每套房屋的月租金定价为4500元或3500元时,租赁公司的月租金可达到315000元.
14.(1)设全天包车数的月平均增长率为,
根据题意可得:,
解得:,(不合题意舍去),
答:全天包车数的月平均增长率为;
(2)根据题意可得:,
化简得:,
解得:,.
答:当租金降价10元或70元时,公司将获利8800元.
15.(1)(件.
故答案为:24.
(2)设每件商品降价元,则平均每天可销售件,
依题意,得:,
整理,得:,
解得:,.
当时,,
舍去.
定价(元
答:当每件商品定价70元时,该商店每天销售利润为1200元.
16.设第一部分的边长为x(0<x<3)cm,则第四部分的边长为(6﹣x)cm,
依题意得:x2+(6﹣x)2=3[x(6﹣x)+x(6﹣x)],
整理得:2x2﹣12x+9=0,
解得:x1=,x2=(不合题意,舍去).
答:第一部分的边长为cm.
17.(1)设该商品平均每月的价格增长率为,
依题意,得:,
解得:,(不合题意,舍去).
答:该商品平均每月的价格增长率为.
(2)依题意,得:,
整理,得:,
解得:,.
商家需尽快将这批商品售出,
.
答:为60元时商品每天的利润可达到4000元.
18.设每千克降低元,超市每天可获得销售利润3640元,由题意得,
,
整理得,
或.
要尽可能让顾客得到实惠,
,
售价为元千克.
答:水果的销售价为每千克29元时,超市每天可获得销售利润3640元.
19.(1)可猜想与是一次函数关系,设这个一次函数为,
这个一次函数的图象经过、这两点,
,
解得,
函数关系式是.
(2)设工艺厂试销该工艺品实际售价为元,
依题意得:,
解得,,(舍,
所以,当售价为30元时,利润为8000元.
20.(1)设与的函数关系式为,
依题意,得解得
所以与的函数关系式为.
(2)依题知.
整理方程,得.
解得,.
此设备的销售单价不得高于35万元,
(舍,所以.
答:该设备的销售单价应是27 万元.
21.(1)解:根据题意得:,
则,
解得:,,
当时,时,,
墙可利用的最大长度为,舍去.
答:的长为.
(2)解:不能围成这样的花圃.理由如下:
依题意可知:,
即,△,
所以方程无实数根,
答:不能围成这样的花圃.
22.(1)设年平均增长率为,由题意得:
,
解得:,(舍去).
答:东部华侨城景区2019至2021年春节长假期间接待游客人次的平均增长率为.
(2)设每杯售价定为元,由题意得:
,
解得:,.
为了能让顾客获得最大优惠,故取20.
答:每杯售价定为20元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额.
23.(1)(米.
故答案为:24.
(2)设米,则米,
依题意得:,
整理得:,
解得:,.
当时,(米,,不合题意,舍去;
当时,(米,符合题意.
答:边的长为10米.
(3)不能,理由如下:
设米,则米,
依题意得:,
整理得:.
△,
该方程没有实数根,
饲养场的面积不能达到210平方米.
24.(1)设的长度为,则,
依题意得:,
解得:,.
墙的长为,
不合题意,舍去,
.
答:在墙上借用的的长度为.
(2)设的长为,则,
依题意得:,
解得:,(不合题意,舍去),
.
答:的长为.
