2023年江苏省泰州市九年级数学中考三轮复习训练题(含答案)
文档属性
| 名称 | 2023年江苏省泰州市九年级数学中考三轮复习训练题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 445.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 15:54:17 | ||
图片预览




文档简介
江苏省泰州市2023年春九年级数学中考三轮复习综合复习训练题(附答案)
一、选择题(本共24分.)
1.2的倒数是( )
A.﹣2 B.2 C. D.﹣
2.下列运算正确的是( )
A.a2+a3=a5 B.(﹣2x)3=﹣2x3
C.(a﹣b)(﹣a+b)=﹣a2﹣2ab﹣b2 D.+=3
3.如图所示图形中既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
4.下列事件:①在体育中考中小明考了满分;②抛掷两枚正方体骰子的点数和大于1;③经过有交通信号灯的路口遇到红灯;④四边形的外角和为180度.其中属于随机事件的个数是( )
A.1个 B.2个 C.3个 D.4个
5.一次函数y=(3﹣a)x+6中,y随自变量x的增大而增大,那么a的取值范围为( )
A.a<3 B.a>3 C.a<﹣3 D.a>﹣3
6.在平面直角坐标系中,一次函数y=﹣2x+b(b为常数)的图象与x、y轴分别交于点A、B,直线AB与双曲线分别交于点P、Q,则AP BP的值是( )
A.4 B.8
C.10 D.与b的取值有关
7.如图,P为⊙O外一点,过点P作⊙O的切线PC、PD,与过圆心O的直线交于A、B两点,点C、D为切点,线段OB交⊙O于点E.若∠APB=90°,tanA=,BE=﹣2,则OP的长度为( )
A. B. C.2 D.
8.如图1,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图2所示,则图2中的a等于( )
A.25 B.20 C.12 D.
二、填空题(共24分.)
9.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .
10.若代数式有意义,则实数x的取值范围是 .
11.一组数据1,0,2,1的方差S2= .
12.因式分解a(a﹣4b)+4b2的结果是 .
13.已知m是负整数,关于x的一元二次方程x2﹣2mx﹣4=0的两根是x1,x2,若x1+x2>x1x2,则m的值等于 .
14.如图所示网格中,每个小正方形的边长都为1,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
15.如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥CD,垂足分别为E、F,若OF=,则AB= .
16.已知,在平面直角坐标系中,函数y=ax2﹣3ax+2a(a≠0)经过B(n﹣3,y1),C(n,y2),D(n+2,y3)这三点,且总有,则n取值范围是 .
三、解答题(共102分)
17.(1)计算:(2+)0+3tan30°﹣+
(2)先化简,再求值:,其中a2﹣4a+3=0.
18.某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).
甲、乙两人连续8次射击成绩统计表
平均成绩(环) 中位数(环) 方差(环2)
甲 7.5
乙 6 3.5
(1)补全统计图和统计表;
(2)如果你是教练,要从甲、乙两人中选一位参加比赛,你会选谁?写出你这样选择的2条理由.
19.一只不透明的袋子中装有1个红球和若干个白球,这些球除颜色外都相同,摇匀后从中任意摸出2个球.
(1)若这个袋子中共有4个球,求摸出红球的概率;
(2)若这个袋子中共有n(n>1且n为正整数)个球,则摸出红球的概率是 (用含n的代数式表示).
20.某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线A﹣B﹣C表示墙面,已知AB⊥BC,AB=3米,BC=9米)和总长为36米的篱笆围建一个“日”形的饲养场BDEF(细线表示篱笆,饲养场中间GH也是用篱笆隔开),如图,点F可能在线段BC上,也可能在线段BC的延长线上.
(1)当点F在线段BC上时,
①设EF的长为x米,则DE= 米(用含x的代数式表示);
②若要求所围成的饲养场BDEF的面积为66平方米,求饲养场EF的长;
(2)饲养场的宽EF为多少米时,饲养场BDEF的面积最大?最大面积为多少平方米?
21.如图,∠ACB=90°,AC=BC,AB为水平边,D为AB边上一点.
(1)只用圆规在B的正上方作一点E,使BE=AD(说明作法,不需要证明);
(2)在(1)的条件下,连接DE,若AC=,AD=3,求DE的长度.
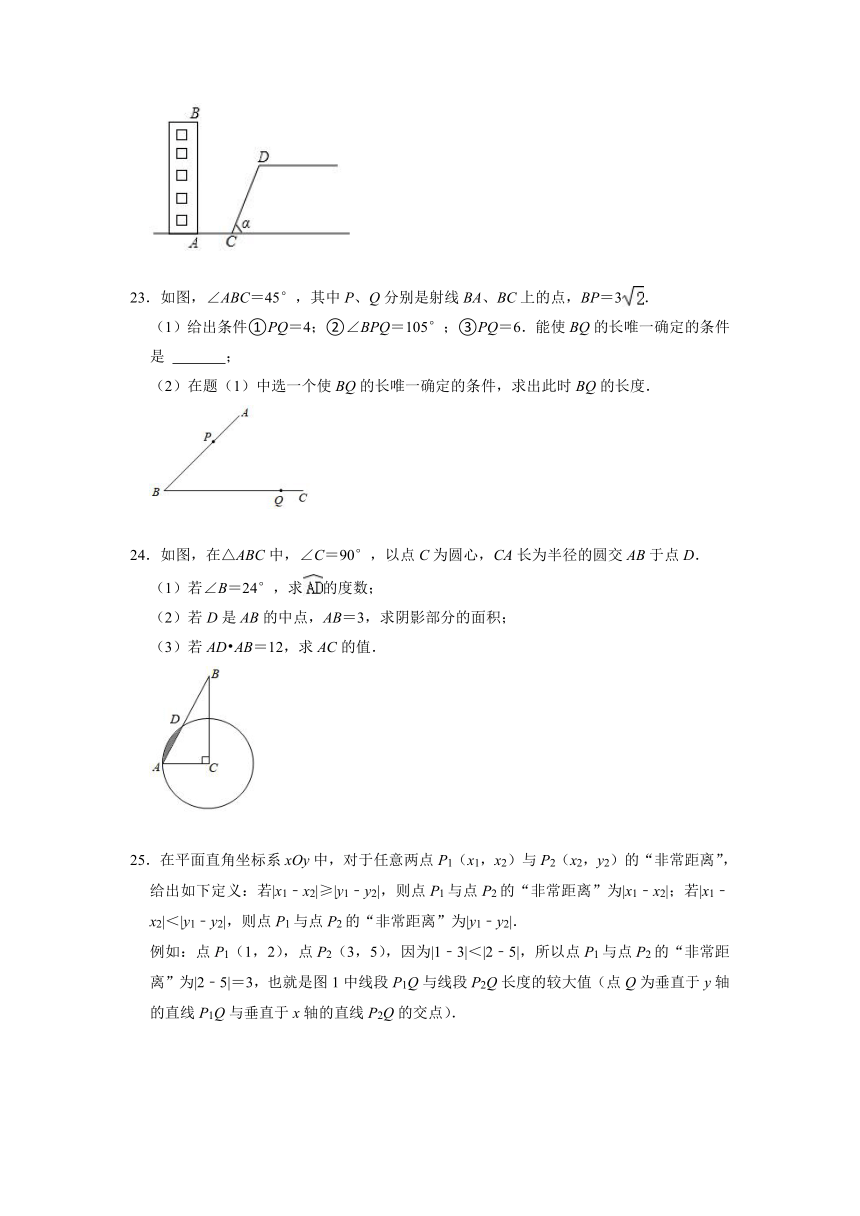
22.如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,≈1.41,≈1.73,≈2.24)
23.如图,∠ABC=45°,其中P、Q分别是射线BA、BC上的点,BP=3.
(1)给出条件①PQ=4;②∠BPQ=105°;③PQ=6.能使BQ的长唯一确定的条件是 ;
(2)在题(1)中选一个使BQ的长唯一确定的条件,求出此时BQ的长度.
24.如图,在△ABC中,∠C=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=24°,求的度数;
(2)若D是AB的中点,AB=3,求阴影部分的面积;
(3)若AD AB=12,求AC的值.
25.在平面直角坐标系xOy中,对于任意两点P1(x1,x2)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(﹣,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标 ;
②直接写出点A与点B的“非常距离”的最小值 ;
(2)已知C是直线y=x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E和点C的坐标.
26.如图,已知抛物线y=﹣x2+mx+n和直线y=x,抛物线顶点为A,与y轴交点为B,直线y=x与抛物线对称轴交于点C.
(1)抛物线顶点坐标为 (用m,n表示);
(2)当抛物线的顶点落在直线y=2x+1上时,求n的最大值.
(3)若四边形ABOC为平行四边形,
①求m的值.
②若直线y=x与抛物线在对称轴右侧部分的交点为D,当△BOD为直角三角形时,求n的值.
③过C点作线段CE⊥AC,设CE=a,是否存在实数a值使△ACE的重心恰好落在抛物线上,若存在直接写出a和n的关系式,若不存在,请说明理由.
参考答案
一、选择题(共24分)
1.解:2的倒数是,
故选:C.
2.解:A、不是同类项,不能合并,错误;
B、(﹣2)3=﹣8x3,错误;
C、(a﹣b)(﹣a+b)=﹣a2+2ab﹣b2,错误;
D、+=+2=3,正确.
故选:D.
3.解:A.不是轴对称图形,是中心对称图形,故本选项不符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
4.解:①在体育中考中,小明考了满分是随机事件;
②抛掷两枚正方体骰子,点数和大于1是必然事件;
③经过有交通信号灯的路口,遇到红灯是随机事件;
④四边形的外角和为180度是不可能事件,
故选:B.
5.解:∵一次函数y=(3﹣a)x+6,函数值y随自变量x的增大而增大,
∴3﹣a>0,解得a<3.
故选:A.
6.解:过点P作PC⊥OB于点C,PD⊥OA与点D,如图,
设点P(m,),则PC=m,PD=.
∵PC⊥OB,PD⊥OA,OB⊥OA,
∴四边形ODPC为矩形.
∴OC=PD=.
∵直线AB与双曲线分别交于点P,
∴=﹣2m+b.
∴m(b﹣2m)=4.
∴m(﹣m)=2.
对于一次函数y=﹣2x+b,令x=0,则y=b,
∴B(0,b).
∴OB=b.
令y=0,则x=,
∴A(,0).
∴OA=.
∴AD=OA﹣OD=.
∴AB==b.
∵PB∥OA,
∴.
∴.
∴PB=m.
∵PD∥OB,
∴.
∴.
∴PA=(﹣m).
∴PA BP=(﹣m)m=5m(﹣m)=10.
故选:C.
7.解:连接OD、OC,
∵PC、PD为⊙O的切线,
∴OD⊥PB,OC⊥PA,PD=PC,
∵∠APB=90°,
∴四边形PDOC为正方形,
设OC=r,
∵tanA=,
∴=,
∴AC=r,
∴PA=r,
∵tanA=,
∴=,
∴PB=r,
∴AB==r,
在Rt△AOC中,OA==r,
∴BE=r﹣r﹣r,
则r﹣r﹣r=﹣2,
解得:r=2,
∴OP=OC=2,
故选:C.
8.解:如图2,
x=5时,BC=5,
x=10时,BC+CD=10,则CD=5,
x=18时,CB+CD+BD=18,则BD=8,
如下图,过点C作CH⊥BD交于H,
在Rt△CDH中,
∵CD=BC,CH⊥BD,
∴DH=BD=4,而CD=5,故CH=3,
当x=5时,点P与点C重合,即BP=5,
a=S△ABP=S△ABC=BD×CH=×8×3=12,
故选:C.
二、填空题(共24分.)
9.解:0.0000025=2.5×10﹣6,
故答案为:2.5×10﹣6.
10.解:∵代数式有意义,
∴x+3≥0,即x≥﹣3.
故答案为:x≥﹣3.
11.解:=(1+0+2+1)=1,
则S2=[(1﹣1)2+(0﹣1)2+(2﹣1)2+(1﹣1)2]=0.5,
故答案为:0.5.
12.解:原式=a2﹣4ab+4b2=(a﹣2b)2,
故答案为:(a﹣2b)2.
13.解:∵关于x的一元二次方程x2﹣2mx﹣4=0的两根是x1,x2,
∴x1+x2=2m,x1x2=﹣4,
∴﹣4<2m<0,
∵m是负整数,
∴m=﹣1,
故答案为:﹣1.
14.解:如图,延长AP到格点C,连接BC,
∵PC=BC=,PB==,
∴PC2+BC2=PB2,
∴△PBC是等腰直角三角形,
∴∠CPB=45°,
∵∠CPB=∠PAB+∠PBA,
∴∠PAB+∠PBA=45°.
故答案为:45.
15.解:作直径DG,连接CG,如图,
∵DG为直径,
∴∠DCG=90°,
∴∠CDG+∠G=90°,
∵AC⊥BD,
∴∠DAC+∠ADB=90°,
∵∠DAC=∠G,
∴∠ADB=∠CDG,
∴=,
∴AB=CG,
∵OF⊥CD,
∴DF=CF,
∵OD=OG,
∴OF为△DCG的中位线,
∴CG=2OF=2×=5,
∴AB=5.
故答案为5.
16.解:∵抛物线解析式为y=ax2﹣3ax+2a=a(x﹣)2﹣,
∴顶点坐标为(,﹣),
∵总有,
∴抛物线开口向下,
当点C在对称轴上或左边,点D在对称轴右边时,
,
解得:<n≤,
当点C在对称右边,点B在对称轴左边时,
,
解得:<n<2,
综上所述,<n<2.
故答案为:<n<2.
三、解答题(共102分)
17.解:(1)原式=1+3×﹣(2﹣)+2
=1+﹣2++2
=1+2;
(2)原式=÷()
=
=,
∵a2﹣4a+3=0,
(a﹣1)(a﹣3)=0,
∴a=1或a=3,
又∵a(a+3)(a﹣3)≠0,
∴a≠0,a≠﹣3,a≠3,
当a=1时,
原式==.
18.解:(1)6×8﹣(4+3+5+6+7+6+8)=9(环),
甲的平均数:(8+8+8+7+8+6+5+6)÷8=7(环),
乙的中位数为:(6+6)÷2=6(环),
甲的方差:×[4×(8﹣7)2+(7﹣7)2+2×(6﹣7)2+(5﹣7)2]=1.25;
图表补全:
平均成绩(环) 中位数(环) 方差(环2)
甲 7 7.5 1.25
乙 6 6 3.5
故答案为:7,6,1.25;
(2)要从甲、乙两人中选一位参加比赛,会选甲,
理由:∵甲的平均成绩、中位数比乙的都高,而且甲成绩的方差较小,甲的成绩较稳定.
∴应选甲运动员.
19.解:(1)记袋中的3个白球分别为白1,白2,白3,从袋中随机摸出2个球,共有6种等可能的情况,
分别是(红,白1)(红,白2)(红,白3)(白1,白2)(白1,白3)(白2,白3),
满足摸出红球的结果有3种,因此摸出红球的概率是=;
(2)这个袋子中共有n(n>1且n为正整数)个球,则摸出红球的概率是.
故答案为:.
20.解:(1)①设EF的长为x米,
∵点F在线段BC上,
∴DE=36﹣2x﹣(x﹣3)=(39﹣3x)(米).
∵BC≤9,即DE≤9,
∴x≥10,
故答案为:(39﹣3x)(x≥10);
②设EF的长为x米,
x(39﹣3x)=66,
3x2﹣39x+66=0,
(x﹣11)(3x﹣6)=0,
x1=11,x2=2(不合题意,舍去),
答:饲养场的长EF为11米;
(2)设饲养场BDEF的面积为S,EF的长为x米,
①点F在线段BC上,
则S=x(39﹣3x)=﹣3x2+39x=﹣3(x﹣)2+,
∵a=﹣3<0,
∴x=时,S有最大值,S最大值=,x≥时,S随x的增大而减小,
∵BC=9米,
∴BF=39﹣3x≤9,解得:x≥10,
∴x=10时,S有最大值,S最大值=﹣3×102+39×10=90(平方米);
②点F在线段BC的延长线上,
则S=(39﹣3x+9)x=﹣x2+24x=﹣(x﹣8)2+96,
∵a=﹣<0,
∴x=8时,S有最大值,S最大值=96,BF=(39﹣3x+9)=12,
∴x=8时,S最大值=96(平方米);
∵96>90,
∴饲养场的宽EF为8米时,饲养场BDEF的面积最大,最大面积为96平方米.
答:饲养场的宽EF为8米时,饲养场BDEF的面积最大,最大面积为96平方米.
21.解:(1)如图,线段BE即为所求.
步骤:①过点B作BJ⊥BA.
②在射线BJ上,截取BE,使得BE=AD.
线段BE即为所求.
(2)∵∠ACB=90°,CA=CB=4,
∴AB=AC=8,
∵AD=3,
∴BD=AB=AD=8﹣3=5,
∵∠DBE=90°,BE=AD=3,
∴DE===.
22.解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CD sin60°=12×=6米,CE=CD cos60°=12×=6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6米.
∵∠D′CE′=39°,
∴CE′=≈≈12.8,
∴EE′=CE′﹣CE=12.8﹣6=6.8≈7(米).
答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.
23.解:(1)唯一确定三角形的条件有:已知三边,已知两边及其夹角,已知两角一边.
故只有②满足两角一边.另外,当PQ=6时,PQ>3,BQ也能唯一确定
故答案为:②③
(2)如图:如在②的条件下:
作PD⊥BC于D,连接PQ.
∵BP=3,∠ABC=45°.
∴∠BPD=45°,BD=PD==3.
∵∠BPQ=105°.
∴∠DPQ=105°﹣45°=60°.
∴DQ=PD=3.
∴BQ=BD+DQ=3+3.
在③的条件下:根据勾股定理得:DQ===3.
∴BQ=BD+DQ=3+3.
综上:BQ=3+3.
24.解:(1)连接CD.
∵∠ACB=90°,∠B=24°,
∴∠A=90°﹣24°=66°,
∵CA=CD,
∴∠A=∠CDA=66°,
∴∠ACD=180°﹣2×66°=48°,
∴的度数为48°;
(2)∵∠ACB=90°,AD=DB,
∴CD=AD=DB=AB=,
∵AC=CD,
∴AC=CD=AD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴S阴=S扇形CAD﹣S△ACD=﹣×()2=﹣.
(3)作CH⊥AB于点H.
∵∠A=∠A,∠AHC=∠ACB=90°,
∴△ACH∽△ABC,
∴=,
∴AC2=AH AB,
∵CH⊥AD,
∴AH=DH,
∵AD AB=12,
∴2AH AB=12,
∴AH AB=6,
∴AC2=6,
∵AC>0,
∴AC=.
25.解:(1)①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|﹣﹣0|=≠2,
∴|0﹣y|=2,
解得y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2);
故答案是:(0,2)或(0,﹣2);
②点A与点B的“非常距离”的最小值为.
故答案是:.
(2)①如图2,取点C与点D的“非常距离”的最小值时,根据运算定义“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”知:|x1﹣x2|=|y1﹣y2|.即AC=AD,
∵C是直线y=x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0,x0+3),
∴﹣x0=x0+2,
此时,x0=﹣,
∴点C与点D的“非常距离”的最小值为:|x0|=,
此时C(﹣,);
②当点E在过原点且与直线y=x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则,
解得,
故E(﹣,).
﹣﹣x0=x0+3﹣,
解得x0=﹣,
则点C的坐标为(﹣,),最小值为1.
26.解:(1)y=﹣x2+mx+n=﹣(x﹣)2+n+,
∴抛物线的顶点坐标为(,n+);
故答案为:(,n+);
(2)当抛物线的顶点落在直线y=2x+1上时,n+=2×+1,
∴n=﹣m2+m+1=﹣(m2﹣4m+4)+2=﹣(m﹣2)2+2,
∴当m=2时,n取最大值,最大值为2;
(3)①∵A(,n+),点C在y=x上,
∴C(,),
∵y=﹣x2+mx+n与y轴交于点B,
∴B(0,n),
若四边形ABOC为平行四边形,
∴BO=AC,
∴n=+n﹣,解得m=0或m=2,
∵m=0时,对称轴为x=0,此时A,B重合,故舍去;
∴m=2;此时y=﹣x2+2x+n.
②当△BOD为直角三角形时,分为∠DBP=90°,∠BDO=90°两种情况:
如图,设AC于x轴交于点F,
∵C(,),
∴CF=OF=,
∴∠COF=∠OCF=45°,
∴∠BOD=45°.
当∠DBO=90°时,BD⊥y轴,
∴BD=OB,
∵OB=n,
∴BD=n,
∴D(n,n),
代入y=﹣x2+2x+n,
解得n=0或n=2,
∵D在对称轴右侧部分,
∴n=2,
当∠BDO=90°时,
如图,过点D作DM⊥y轴,垂足为M,
∵∠BOD=45°,
∴∠OBD=45°,
∴BD=OD,
∴DM=OB=,
∴OM=OB=,
代入y=﹣x2+2x+n,
解得n=0或n=6,
∵D在对称轴右侧部分,
∴n=6,
综上所述,n=2或n=6.
③存在,理由如下:
如图,过点C作线段CE⊥AC,设点E在抛物线的左侧,根据抛物线的对称性可知,点E在抛物线的右侧和左侧一致,设AE的中点为P,CE的中点为Q,AQ和CP的交点即为△AEC的重心G,
∵CE=a,C(1,1),
∴E(1﹣a,1),
∵y=﹣x2+2x+n,
∴A(1,n+1).
∴P(,),即P(1﹣,1+),Q(1﹣,1).
∴直线AQ的解析式为:y=x+n+1﹣,
直线CP的解析式为:y=﹣x+1+,
令x+n+1﹣=﹣x+1+,
解得x=1﹣,
∴G(1﹣,1+),
∵△ACE的重心恰好落在抛物线y=﹣x2+2x+n上,
∴1+=﹣(1﹣)2+2×(1﹣)+n,
整理得,a2=6n.
∴a和n的关系式为:a2=6n.
一、选择题(本共24分.)
1.2的倒数是( )
A.﹣2 B.2 C. D.﹣
2.下列运算正确的是( )
A.a2+a3=a5 B.(﹣2x)3=﹣2x3
C.(a﹣b)(﹣a+b)=﹣a2﹣2ab﹣b2 D.+=3
3.如图所示图形中既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
4.下列事件:①在体育中考中小明考了满分;②抛掷两枚正方体骰子的点数和大于1;③经过有交通信号灯的路口遇到红灯;④四边形的外角和为180度.其中属于随机事件的个数是( )
A.1个 B.2个 C.3个 D.4个
5.一次函数y=(3﹣a)x+6中,y随自变量x的增大而增大,那么a的取值范围为( )
A.a<3 B.a>3 C.a<﹣3 D.a>﹣3
6.在平面直角坐标系中,一次函数y=﹣2x+b(b为常数)的图象与x、y轴分别交于点A、B,直线AB与双曲线分别交于点P、Q,则AP BP的值是( )
A.4 B.8
C.10 D.与b的取值有关
7.如图,P为⊙O外一点,过点P作⊙O的切线PC、PD,与过圆心O的直线交于A、B两点,点C、D为切点,线段OB交⊙O于点E.若∠APB=90°,tanA=,BE=﹣2,则OP的长度为( )
A. B. C.2 D.
8.如图1,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图2所示,则图2中的a等于( )
A.25 B.20 C.12 D.
二、填空题(共24分.)
9.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .
10.若代数式有意义,则实数x的取值范围是 .
11.一组数据1,0,2,1的方差S2= .
12.因式分解a(a﹣4b)+4b2的结果是 .
13.已知m是负整数,关于x的一元二次方程x2﹣2mx﹣4=0的两根是x1,x2,若x1+x2>x1x2,则m的值等于 .
14.如图所示网格中,每个小正方形的边长都为1,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
15.如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥CD,垂足分别为E、F,若OF=,则AB= .
16.已知,在平面直角坐标系中,函数y=ax2﹣3ax+2a(a≠0)经过B(n﹣3,y1),C(n,y2),D(n+2,y3)这三点,且总有,则n取值范围是 .
三、解答题(共102分)
17.(1)计算:(2+)0+3tan30°﹣+
(2)先化简,再求值:,其中a2﹣4a+3=0.
18.某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).
甲、乙两人连续8次射击成绩统计表
平均成绩(环) 中位数(环) 方差(环2)
甲 7.5
乙 6 3.5
(1)补全统计图和统计表;
(2)如果你是教练,要从甲、乙两人中选一位参加比赛,你会选谁?写出你这样选择的2条理由.
19.一只不透明的袋子中装有1个红球和若干个白球,这些球除颜色外都相同,摇匀后从中任意摸出2个球.
(1)若这个袋子中共有4个球,求摸出红球的概率;
(2)若这个袋子中共有n(n>1且n为正整数)个球,则摸出红球的概率是 (用含n的代数式表示).
20.某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线A﹣B﹣C表示墙面,已知AB⊥BC,AB=3米,BC=9米)和总长为36米的篱笆围建一个“日”形的饲养场BDEF(细线表示篱笆,饲养场中间GH也是用篱笆隔开),如图,点F可能在线段BC上,也可能在线段BC的延长线上.
(1)当点F在线段BC上时,
①设EF的长为x米,则DE= 米(用含x的代数式表示);
②若要求所围成的饲养场BDEF的面积为66平方米,求饲养场EF的长;
(2)饲养场的宽EF为多少米时,饲养场BDEF的面积最大?最大面积为多少平方米?
21.如图,∠ACB=90°,AC=BC,AB为水平边,D为AB边上一点.
(1)只用圆规在B的正上方作一点E,使BE=AD(说明作法,不需要证明);
(2)在(1)的条件下,连接DE,若AC=,AD=3,求DE的长度.
22.如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,≈1.41,≈1.73,≈2.24)
23.如图,∠ABC=45°,其中P、Q分别是射线BA、BC上的点,BP=3.
(1)给出条件①PQ=4;②∠BPQ=105°;③PQ=6.能使BQ的长唯一确定的条件是 ;
(2)在题(1)中选一个使BQ的长唯一确定的条件,求出此时BQ的长度.
24.如图,在△ABC中,∠C=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=24°,求的度数;
(2)若D是AB的中点,AB=3,求阴影部分的面积;
(3)若AD AB=12,求AC的值.
25.在平面直角坐标系xOy中,对于任意两点P1(x1,x2)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(﹣,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标 ;
②直接写出点A与点B的“非常距离”的最小值 ;
(2)已知C是直线y=x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E和点C的坐标.
26.如图,已知抛物线y=﹣x2+mx+n和直线y=x,抛物线顶点为A,与y轴交点为B,直线y=x与抛物线对称轴交于点C.
(1)抛物线顶点坐标为 (用m,n表示);
(2)当抛物线的顶点落在直线y=2x+1上时,求n的最大值.
(3)若四边形ABOC为平行四边形,
①求m的值.
②若直线y=x与抛物线在对称轴右侧部分的交点为D,当△BOD为直角三角形时,求n的值.
③过C点作线段CE⊥AC,设CE=a,是否存在实数a值使△ACE的重心恰好落在抛物线上,若存在直接写出a和n的关系式,若不存在,请说明理由.
参考答案
一、选择题(共24分)
1.解:2的倒数是,
故选:C.
2.解:A、不是同类项,不能合并,错误;
B、(﹣2)3=﹣8x3,错误;
C、(a﹣b)(﹣a+b)=﹣a2+2ab﹣b2,错误;
D、+=+2=3,正确.
故选:D.
3.解:A.不是轴对称图形,是中心对称图形,故本选项不符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
4.解:①在体育中考中,小明考了满分是随机事件;
②抛掷两枚正方体骰子,点数和大于1是必然事件;
③经过有交通信号灯的路口,遇到红灯是随机事件;
④四边形的外角和为180度是不可能事件,
故选:B.
5.解:∵一次函数y=(3﹣a)x+6,函数值y随自变量x的增大而增大,
∴3﹣a>0,解得a<3.
故选:A.
6.解:过点P作PC⊥OB于点C,PD⊥OA与点D,如图,
设点P(m,),则PC=m,PD=.
∵PC⊥OB,PD⊥OA,OB⊥OA,
∴四边形ODPC为矩形.
∴OC=PD=.
∵直线AB与双曲线分别交于点P,
∴=﹣2m+b.
∴m(b﹣2m)=4.
∴m(﹣m)=2.
对于一次函数y=﹣2x+b,令x=0,则y=b,
∴B(0,b).
∴OB=b.
令y=0,则x=,
∴A(,0).
∴OA=.
∴AD=OA﹣OD=.
∴AB==b.
∵PB∥OA,
∴.
∴.
∴PB=m.
∵PD∥OB,
∴.
∴.
∴PA=(﹣m).
∴PA BP=(﹣m)m=5m(﹣m)=10.
故选:C.
7.解:连接OD、OC,
∵PC、PD为⊙O的切线,
∴OD⊥PB,OC⊥PA,PD=PC,
∵∠APB=90°,
∴四边形PDOC为正方形,
设OC=r,
∵tanA=,
∴=,
∴AC=r,
∴PA=r,
∵tanA=,
∴=,
∴PB=r,
∴AB==r,
在Rt△AOC中,OA==r,
∴BE=r﹣r﹣r,
则r﹣r﹣r=﹣2,
解得:r=2,
∴OP=OC=2,
故选:C.
8.解:如图2,
x=5时,BC=5,
x=10时,BC+CD=10,则CD=5,
x=18时,CB+CD+BD=18,则BD=8,
如下图,过点C作CH⊥BD交于H,
在Rt△CDH中,
∵CD=BC,CH⊥BD,
∴DH=BD=4,而CD=5,故CH=3,
当x=5时,点P与点C重合,即BP=5,
a=S△ABP=S△ABC=BD×CH=×8×3=12,
故选:C.
二、填空题(共24分.)
9.解:0.0000025=2.5×10﹣6,
故答案为:2.5×10﹣6.
10.解:∵代数式有意义,
∴x+3≥0,即x≥﹣3.
故答案为:x≥﹣3.
11.解:=(1+0+2+1)=1,
则S2=[(1﹣1)2+(0﹣1)2+(2﹣1)2+(1﹣1)2]=0.5,
故答案为:0.5.
12.解:原式=a2﹣4ab+4b2=(a﹣2b)2,
故答案为:(a﹣2b)2.
13.解:∵关于x的一元二次方程x2﹣2mx﹣4=0的两根是x1,x2,
∴x1+x2=2m,x1x2=﹣4,
∴﹣4<2m<0,
∵m是负整数,
∴m=﹣1,
故答案为:﹣1.
14.解:如图,延长AP到格点C,连接BC,
∵PC=BC=,PB==,
∴PC2+BC2=PB2,
∴△PBC是等腰直角三角形,
∴∠CPB=45°,
∵∠CPB=∠PAB+∠PBA,
∴∠PAB+∠PBA=45°.
故答案为:45.
15.解:作直径DG,连接CG,如图,
∵DG为直径,
∴∠DCG=90°,
∴∠CDG+∠G=90°,
∵AC⊥BD,
∴∠DAC+∠ADB=90°,
∵∠DAC=∠G,
∴∠ADB=∠CDG,
∴=,
∴AB=CG,
∵OF⊥CD,
∴DF=CF,
∵OD=OG,
∴OF为△DCG的中位线,
∴CG=2OF=2×=5,
∴AB=5.
故答案为5.
16.解:∵抛物线解析式为y=ax2﹣3ax+2a=a(x﹣)2﹣,
∴顶点坐标为(,﹣),
∵总有,
∴抛物线开口向下,
当点C在对称轴上或左边,点D在对称轴右边时,
,
解得:<n≤,
当点C在对称右边,点B在对称轴左边时,
,
解得:<n<2,
综上所述,<n<2.
故答案为:<n<2.
三、解答题(共102分)
17.解:(1)原式=1+3×﹣(2﹣)+2
=1+﹣2++2
=1+2;
(2)原式=÷()
=
=,
∵a2﹣4a+3=0,
(a﹣1)(a﹣3)=0,
∴a=1或a=3,
又∵a(a+3)(a﹣3)≠0,
∴a≠0,a≠﹣3,a≠3,
当a=1时,
原式==.
18.解:(1)6×8﹣(4+3+5+6+7+6+8)=9(环),
甲的平均数:(8+8+8+7+8+6+5+6)÷8=7(环),
乙的中位数为:(6+6)÷2=6(环),
甲的方差:×[4×(8﹣7)2+(7﹣7)2+2×(6﹣7)2+(5﹣7)2]=1.25;
图表补全:
平均成绩(环) 中位数(环) 方差(环2)
甲 7 7.5 1.25
乙 6 6 3.5
故答案为:7,6,1.25;
(2)要从甲、乙两人中选一位参加比赛,会选甲,
理由:∵甲的平均成绩、中位数比乙的都高,而且甲成绩的方差较小,甲的成绩较稳定.
∴应选甲运动员.
19.解:(1)记袋中的3个白球分别为白1,白2,白3,从袋中随机摸出2个球,共有6种等可能的情况,
分别是(红,白1)(红,白2)(红,白3)(白1,白2)(白1,白3)(白2,白3),
满足摸出红球的结果有3种,因此摸出红球的概率是=;
(2)这个袋子中共有n(n>1且n为正整数)个球,则摸出红球的概率是.
故答案为:.
20.解:(1)①设EF的长为x米,
∵点F在线段BC上,
∴DE=36﹣2x﹣(x﹣3)=(39﹣3x)(米).
∵BC≤9,即DE≤9,
∴x≥10,
故答案为:(39﹣3x)(x≥10);
②设EF的长为x米,
x(39﹣3x)=66,
3x2﹣39x+66=0,
(x﹣11)(3x﹣6)=0,
x1=11,x2=2(不合题意,舍去),
答:饲养场的长EF为11米;
(2)设饲养场BDEF的面积为S,EF的长为x米,
①点F在线段BC上,
则S=x(39﹣3x)=﹣3x2+39x=﹣3(x﹣)2+,
∵a=﹣3<0,
∴x=时,S有最大值,S最大值=,x≥时,S随x的增大而减小,
∵BC=9米,
∴BF=39﹣3x≤9,解得:x≥10,
∴x=10时,S有最大值,S最大值=﹣3×102+39×10=90(平方米);
②点F在线段BC的延长线上,
则S=(39﹣3x+9)x=﹣x2+24x=﹣(x﹣8)2+96,
∵a=﹣<0,
∴x=8时,S有最大值,S最大值=96,BF=(39﹣3x+9)=12,
∴x=8时,S最大值=96(平方米);
∵96>90,
∴饲养场的宽EF为8米时,饲养场BDEF的面积最大,最大面积为96平方米.
答:饲养场的宽EF为8米时,饲养场BDEF的面积最大,最大面积为96平方米.
21.解:(1)如图,线段BE即为所求.
步骤:①过点B作BJ⊥BA.
②在射线BJ上,截取BE,使得BE=AD.
线段BE即为所求.
(2)∵∠ACB=90°,CA=CB=4,
∴AB=AC=8,
∵AD=3,
∴BD=AB=AD=8﹣3=5,
∵∠DBE=90°,BE=AD=3,
∴DE===.
22.解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CD sin60°=12×=6米,CE=CD cos60°=12×=6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6米.
∵∠D′CE′=39°,
∴CE′=≈≈12.8,
∴EE′=CE′﹣CE=12.8﹣6=6.8≈7(米).
答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.
23.解:(1)唯一确定三角形的条件有:已知三边,已知两边及其夹角,已知两角一边.
故只有②满足两角一边.另外,当PQ=6时,PQ>3,BQ也能唯一确定
故答案为:②③
(2)如图:如在②的条件下:
作PD⊥BC于D,连接PQ.
∵BP=3,∠ABC=45°.
∴∠BPD=45°,BD=PD==3.
∵∠BPQ=105°.
∴∠DPQ=105°﹣45°=60°.
∴DQ=PD=3.
∴BQ=BD+DQ=3+3.
在③的条件下:根据勾股定理得:DQ===3.
∴BQ=BD+DQ=3+3.
综上:BQ=3+3.
24.解:(1)连接CD.
∵∠ACB=90°,∠B=24°,
∴∠A=90°﹣24°=66°,
∵CA=CD,
∴∠A=∠CDA=66°,
∴∠ACD=180°﹣2×66°=48°,
∴的度数为48°;
(2)∵∠ACB=90°,AD=DB,
∴CD=AD=DB=AB=,
∵AC=CD,
∴AC=CD=AD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴S阴=S扇形CAD﹣S△ACD=﹣×()2=﹣.
(3)作CH⊥AB于点H.
∵∠A=∠A,∠AHC=∠ACB=90°,
∴△ACH∽△ABC,
∴=,
∴AC2=AH AB,
∵CH⊥AD,
∴AH=DH,
∵AD AB=12,
∴2AH AB=12,
∴AH AB=6,
∴AC2=6,
∵AC>0,
∴AC=.
25.解:(1)①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|﹣﹣0|=≠2,
∴|0﹣y|=2,
解得y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2);
故答案是:(0,2)或(0,﹣2);
②点A与点B的“非常距离”的最小值为.
故答案是:.
(2)①如图2,取点C与点D的“非常距离”的最小值时,根据运算定义“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”知:|x1﹣x2|=|y1﹣y2|.即AC=AD,
∵C是直线y=x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0,x0+3),
∴﹣x0=x0+2,
此时,x0=﹣,
∴点C与点D的“非常距离”的最小值为:|x0|=,
此时C(﹣,);
②当点E在过原点且与直线y=x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则,
解得,
故E(﹣,).
﹣﹣x0=x0+3﹣,
解得x0=﹣,
则点C的坐标为(﹣,),最小值为1.
26.解:(1)y=﹣x2+mx+n=﹣(x﹣)2+n+,
∴抛物线的顶点坐标为(,n+);
故答案为:(,n+);
(2)当抛物线的顶点落在直线y=2x+1上时,n+=2×+1,
∴n=﹣m2+m+1=﹣(m2﹣4m+4)+2=﹣(m﹣2)2+2,
∴当m=2时,n取最大值,最大值为2;
(3)①∵A(,n+),点C在y=x上,
∴C(,),
∵y=﹣x2+mx+n与y轴交于点B,
∴B(0,n),
若四边形ABOC为平行四边形,
∴BO=AC,
∴n=+n﹣,解得m=0或m=2,
∵m=0时,对称轴为x=0,此时A,B重合,故舍去;
∴m=2;此时y=﹣x2+2x+n.
②当△BOD为直角三角形时,分为∠DBP=90°,∠BDO=90°两种情况:
如图,设AC于x轴交于点F,
∵C(,),
∴CF=OF=,
∴∠COF=∠OCF=45°,
∴∠BOD=45°.
当∠DBO=90°时,BD⊥y轴,
∴BD=OB,
∵OB=n,
∴BD=n,
∴D(n,n),
代入y=﹣x2+2x+n,
解得n=0或n=2,
∵D在对称轴右侧部分,
∴n=2,
当∠BDO=90°时,
如图,过点D作DM⊥y轴,垂足为M,
∵∠BOD=45°,
∴∠OBD=45°,
∴BD=OD,
∴DM=OB=,
∴OM=OB=,
代入y=﹣x2+2x+n,
解得n=0或n=6,
∵D在对称轴右侧部分,
∴n=6,
综上所述,n=2或n=6.
③存在,理由如下:
如图,过点C作线段CE⊥AC,设点E在抛物线的左侧,根据抛物线的对称性可知,点E在抛物线的右侧和左侧一致,设AE的中点为P,CE的中点为Q,AQ和CP的交点即为△AEC的重心G,
∵CE=a,C(1,1),
∴E(1﹣a,1),
∵y=﹣x2+2x+n,
∴A(1,n+1).
∴P(,),即P(1﹣,1+),Q(1﹣,1).
∴直线AQ的解析式为:y=x+n+1﹣,
直线CP的解析式为:y=﹣x+1+,
令x+n+1﹣=﹣x+1+,
解得x=1﹣,
∴G(1﹣,1+),
∵△ACE的重心恰好落在抛物线y=﹣x2+2x+n上,
∴1+=﹣(1﹣)2+2×(1﹣)+n,
整理得,a2=6n.
∴a和n的关系式为:a2=6n.
同课章节目录
