广东省深圳市海滨中学八年级数学下册教学课件:中心对称(共29张PPT)
文档属性
| 名称 | 广东省深圳市海滨中学八年级数学下册教学课件:中心对称(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 273.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-30 19:01:35 | ||
图片预览




文档简介
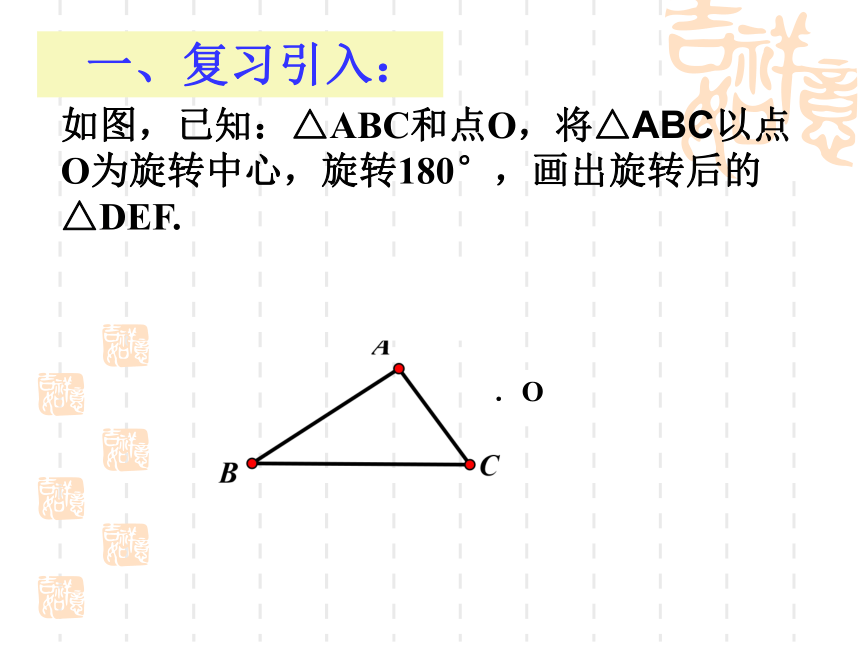
课件29张PPT。 第三章 图形的平移与旋转 第3节 中心对称 .O如图,已知:△ABC和点O,将△ABC以点
O为旋转中心,旋转180°,画出旋转后的
△DEF. 一、复习引入: 二、探索新知 1、观察图3-18,图(1)经过怎样的运动变化可以与图(2)重合?(第一部分)将每幅图中的对应点连成线段,你发现什么了?zxxk
2、定义:
如果把一个图形绕着某一点旋转180°,它能与另一个图形重合,那么这两个图形关于这个点对称或中心对称. 这个点叫它们的对称中心. 简称:两个图形成中心对称. Zxx.k
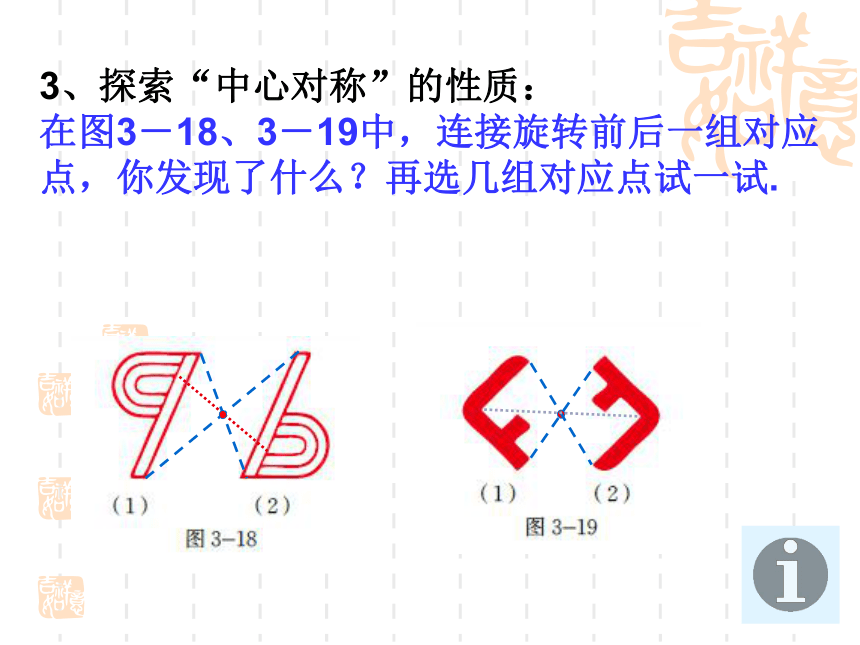
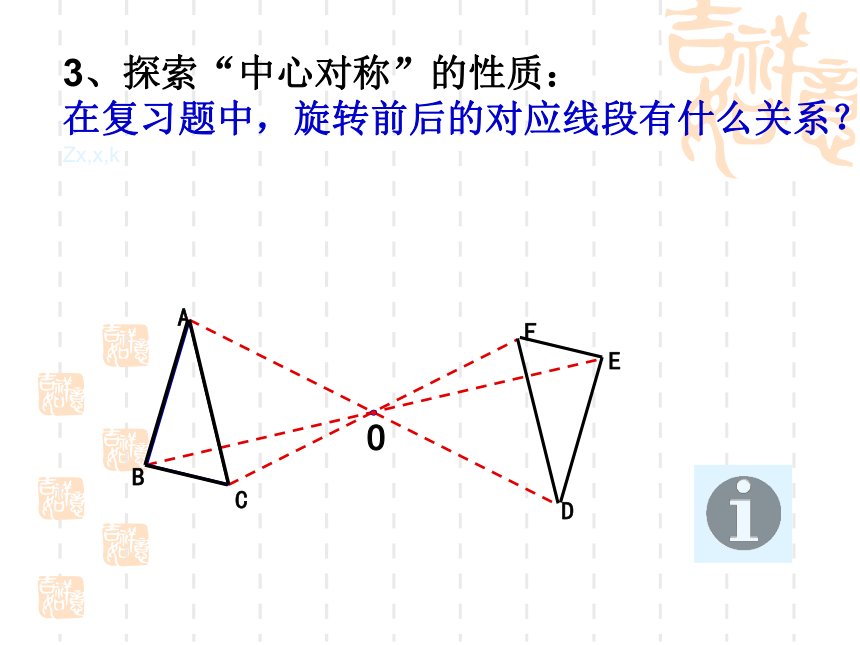
3、探索“中心对称”的性质:
在图3-18、3-19中,连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试.3、探索“中心对称”的性质:
在复习题中,旋转前后的对应线段有什么关系?Zx,x,k
“中心对称”的性质:(1)关于中心对称的两个图形是全等图形;
(2)关于中心对称的两个图形,对称点所连
线段都经过对称中心,而且被对称中心
平分.
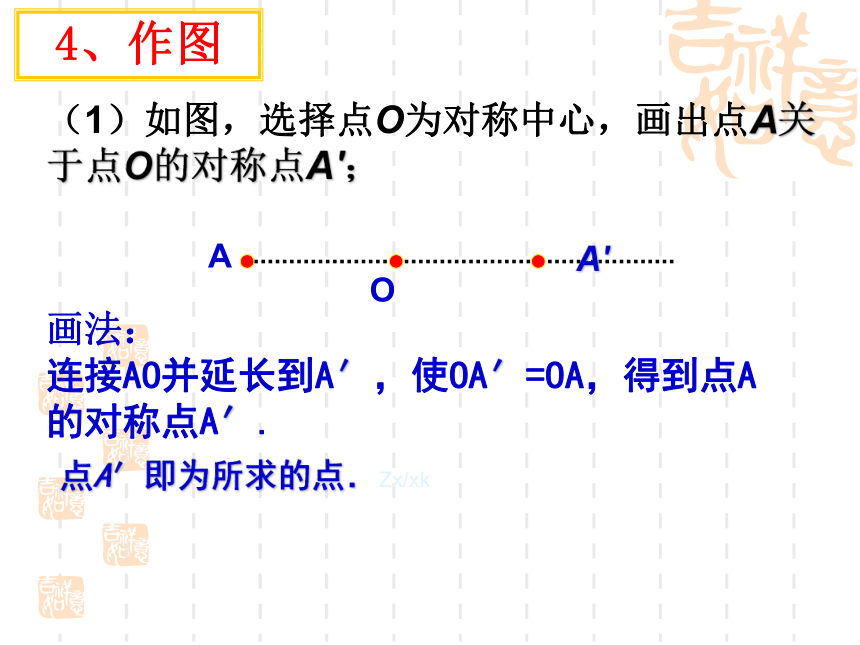
(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;画法:
连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.点A′即为所求的点.Zx/xk
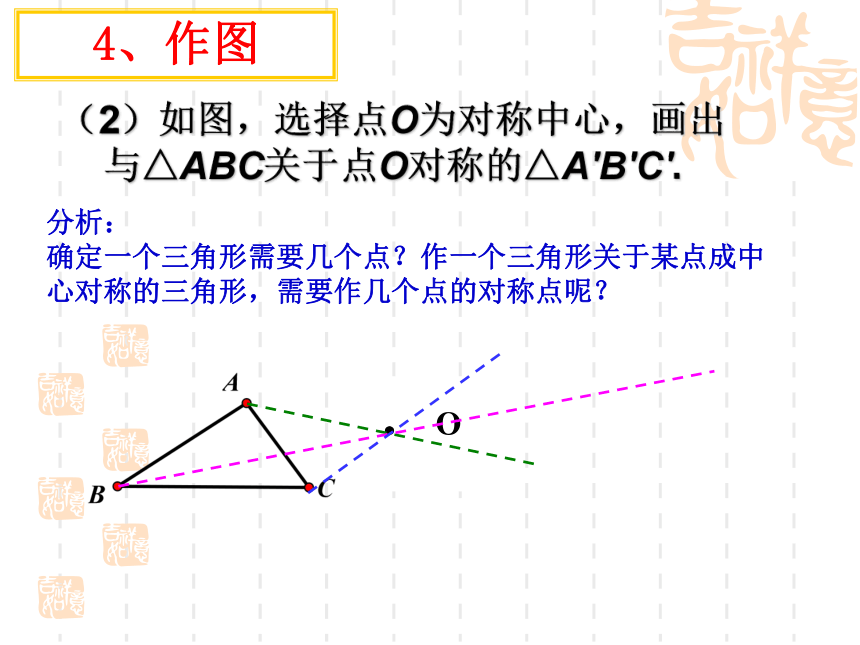
4、作图AA′ O(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.分析:
确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢? .O4、作图例题:
如图,点O是线段AE的中点,以O为对称中心,画出与五边形ABCDE成中心对称的图形. 4、作图轴 对 称中 心 对 称123翻转后和另一个图形重合旋转后和另一个图形重合 5、中心对称与轴对称的联系与区别第二部分:中心对称图形 1、议一议:
观察P82图3-23,这些图形有什么共同特征?2、“中心对称图形”概念:把一个图形绕某个点旋转 180°,如果旋转后的图形能与原来的图形 重合 ,
那么这个图形叫做中心对称图形 ; 这个点叫 对称中心 .3、两个图形成中心对称与中心对称图形的联系与区别:区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形,则它们成中心对称. 三、课堂练习:1、(1)下面图形哪些是中心对称图形?(2)下面扑克牌中,哪些牌面是中心对称图形?2、在26个英文大写正体字母中,哪些字母是中心对称图形?
3、下列图形中,既是轴对称图形,又是中心对称图形的是( )
4、在平面直角坐标系中,已知点P坐标为(2,3),
求:
(1)点P关于y轴的对称点P1的坐标是: ,
(2) 点P关于x轴的对称点P2的坐标是: ;
(3) 点P关于原点的对称点P3的坐标是: .
5、如图已知:△ABO.
(1)以O为对称中心,画出与△ABO成中心对称的△CDO;
(2)连接BC、AD,四边形ABCD是中心对称图形吗?是轴对称图形吗?如图Rt△ABC中,BC=AC=4,将△ABC
沿CB方向移动到△A`B`C`位置;D 例题(1)若平移距离为3,
①求两个三角形重叠部分的周长;
②四边形ABB`A`是怎样的四边形?它的面积是多少? 如图Rt△ABC中,BC=AC=4,将△ABC
沿CB方向移动到△A`B`C`位置;(2)若平移距离为 x(0<x<4) ,两个三角形
重叠部分的面积为y,
①写出y关于x的函数关系式,
②求出平移距离为3时重叠三角形的面积.D 例题 小明和妈妈在广场游玩时, 看见许多喷水嘴正在给草坪浇水。 喷水嘴不停地旋转着, 但每时每刻喷出的水雾总是四分之一圆。妈妈问:“小明,如果喷出水雾的范围内有一正方形, 喷水嘴位于它的中心, 你知道喷水嘴在旋转的过程中瞬时浇过正方形区域的面积是多少吗? ”
同学们,请你替小明做出回答。C2、如图,正方形ABCD边长为 4,沿对角线所在直线 l 将该正方形向右平移到EFGH的位置,已知△ODH的面积为9/2,求平移的距离.lABCEDFGHOP
O为旋转中心,旋转180°,画出旋转后的
△DEF. 一、复习引入: 二、探索新知 1、观察图3-18,图(1)经过怎样的运动变化可以与图(2)重合?(第一部分)将每幅图中的对应点连成线段,你发现什么了?zxxk
2、定义:
如果把一个图形绕着某一点旋转180°,它能与另一个图形重合,那么这两个图形关于这个点对称或中心对称. 这个点叫它们的对称中心. 简称:两个图形成中心对称. Zxx.k
3、探索“中心对称”的性质:
在图3-18、3-19中,连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试.3、探索“中心对称”的性质:
在复习题中,旋转前后的对应线段有什么关系?Zx,x,k
“中心对称”的性质:(1)关于中心对称的两个图形是全等图形;
(2)关于中心对称的两个图形,对称点所连
线段都经过对称中心,而且被对称中心
平分.
(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;画法:
连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.点A′即为所求的点.Zx/xk
4、作图AA′ O(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.分析:
确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢? .O4、作图例题:
如图,点O是线段AE的中点,以O为对称中心,画出与五边形ABCDE成中心对称的图形. 4、作图轴 对 称中 心 对 称123翻转后和另一个图形重合旋转后和另一个图形重合 5、中心对称与轴对称的联系与区别第二部分:中心对称图形 1、议一议:
观察P82图3-23,这些图形有什么共同特征?2、“中心对称图形”概念:把一个图形绕某个点旋转 180°,如果旋转后的图形能与原来的图形 重合 ,
那么这个图形叫做中心对称图形 ; 这个点叫 对称中心 .3、两个图形成中心对称与中心对称图形的联系与区别:区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形,则它们成中心对称. 三、课堂练习:1、(1)下面图形哪些是中心对称图形?(2)下面扑克牌中,哪些牌面是中心对称图形?2、在26个英文大写正体字母中,哪些字母是中心对称图形?
3、下列图形中,既是轴对称图形,又是中心对称图形的是( )
4、在平面直角坐标系中,已知点P坐标为(2,3),
求:
(1)点P关于y轴的对称点P1的坐标是: ,
(2) 点P关于x轴的对称点P2的坐标是: ;
(3) 点P关于原点的对称点P3的坐标是: .
5、如图已知:△ABO.
(1)以O为对称中心,画出与△ABO成中心对称的△CDO;
(2)连接BC、AD,四边形ABCD是中心对称图形吗?是轴对称图形吗?如图Rt△ABC中,BC=AC=4,将△ABC
沿CB方向移动到△A`B`C`位置;D 例题(1)若平移距离为3,
①求两个三角形重叠部分的周长;
②四边形ABB`A`是怎样的四边形?它的面积是多少? 如图Rt△ABC中,BC=AC=4,将△ABC
沿CB方向移动到△A`B`C`位置;(2)若平移距离为 x(0<x<4) ,两个三角形
重叠部分的面积为y,
①写出y关于x的函数关系式,
②求出平移距离为3时重叠三角形的面积.D 例题 小明和妈妈在广场游玩时, 看见许多喷水嘴正在给草坪浇水。 喷水嘴不停地旋转着, 但每时每刻喷出的水雾总是四分之一圆。妈妈问:“小明,如果喷出水雾的范围内有一正方形, 喷水嘴位于它的中心, 你知道喷水嘴在旋转的过程中瞬时浇过正方形区域的面积是多少吗? ”
同学们,请你替小明做出回答。C2、如图,正方形ABCD边长为 4,沿对角线所在直线 l 将该正方形向右平移到EFGH的位置,已知△ODH的面积为9/2,求平移的距离.lABCEDFGHOP
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
