实数与向量的乘积[上学期]
图片预览


文档简介
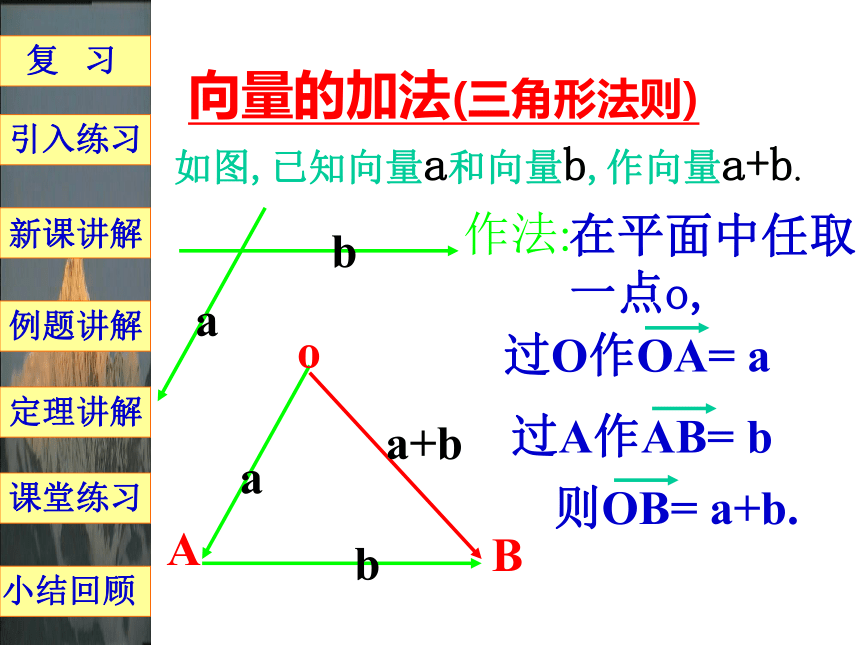
课件13张PPT。 实数与向量的积第一课时主讲: 郭兴刚向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取
一点o,o 复 习例题讲解小结回顾引入练习
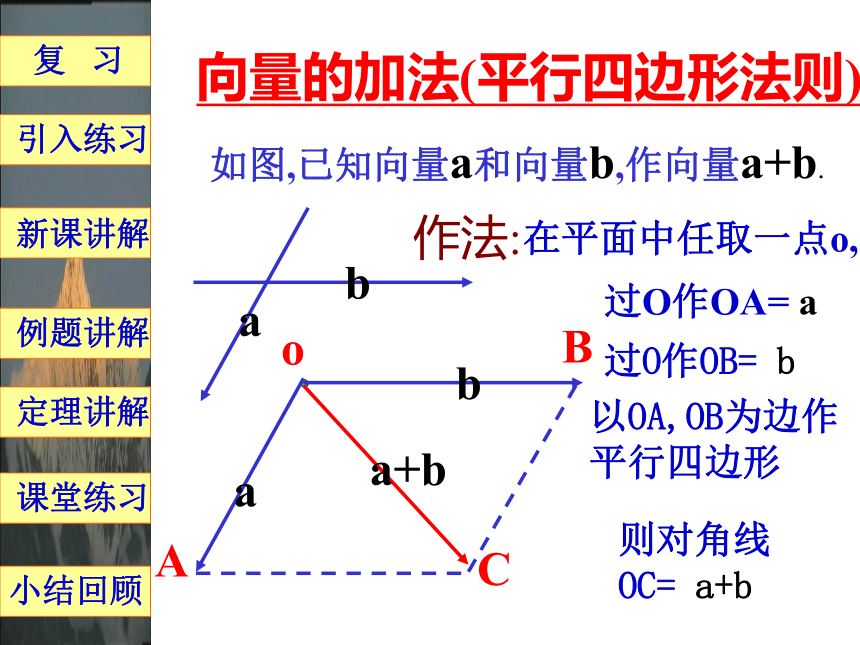
新课讲解定理讲解课堂练习向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取一点o,过O作OA= a过O作OB= bb以OA,OB为边作
平行四边形则对角线
OC= a+b 复 习例题讲解小结回顾引入练习
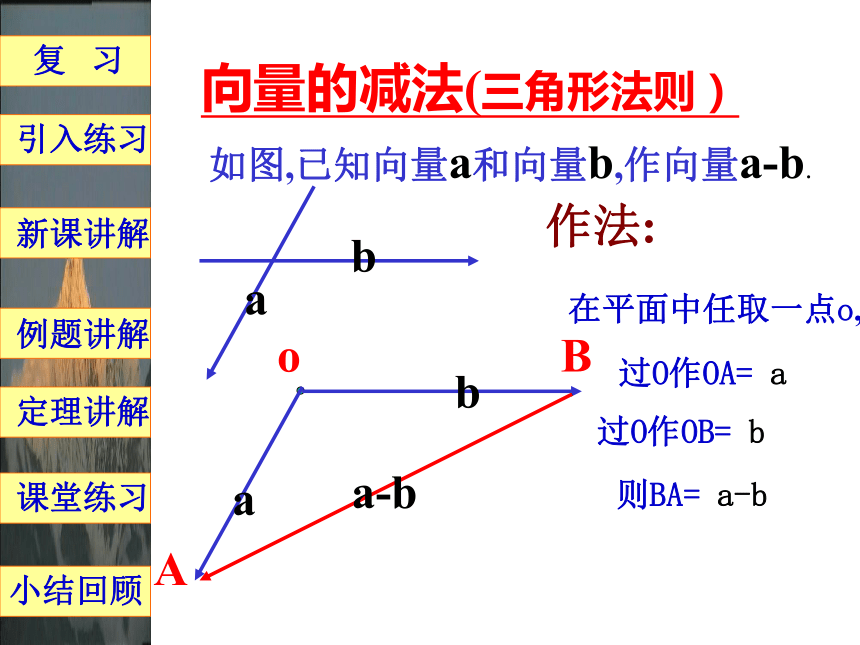
新课讲解定理讲解课堂练习向量的减法(三角形法则)如图,已知向量a和向量b,作向量a-b.b作法:在平面中任取一点o,过O作OA= a过O作OB= b则BA= a-b 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习定义:一般地,实数λ与向量a的积是一个向量,记作
λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习 例1 计算:
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)答案:-12a5b-a+5b-2c 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习共线向量的充要条件:对于向量 a (a≠0), b ,以及实数λ,μ问题1:如果 b=λa ,
那么,向量a与b是否共线?问题2:如果 向量a与b共线
那么,b=λa ?定理:向量 b 与非零向量 a 共线的充要条件是
有且只有一个实数λ,使得 b=λa 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习课本P105- 4定理:向量 b 与非零向量 a 共线的充要条件是有且只
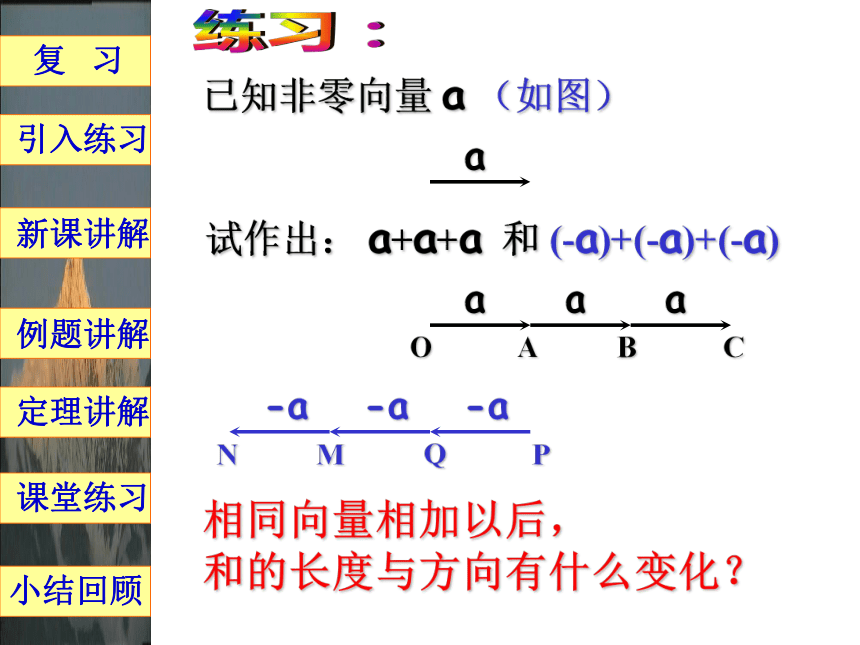
有一个实数λ,使得 b=λa 练习: 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习练习题: 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习作业布置:课本 :
第 3题
P108 第 4题
第 5题
复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习
一点o,o 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取一点o,过O作OA= a过O作OB= bb以OA,OB为边作
平行四边形则对角线
OC= a+b 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习向量的减法(三角形法则)如图,已知向量a和向量b,作向量a-b.b作法:在平面中任取一点o,过O作OA= a过O作OB= b则BA= a-b 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习定义:一般地,实数λ与向量a的积是一个向量,记作
λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习 例1 计算:
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)答案:-12a5b-a+5b-2c 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习共线向量的充要条件:对于向量 a (a≠0), b ,以及实数λ,μ问题1:如果 b=λa ,
那么,向量a与b是否共线?问题2:如果 向量a与b共线
那么,b=λa ?定理:向量 b 与非零向量 a 共线的充要条件是
有且只有一个实数λ,使得 b=λa 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习课本P105- 4定理:向量 b 与非零向量 a 共线的充要条件是有且只
有一个实数λ,使得 b=λa 练习: 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习练习题: 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习 复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习作业布置:课本 :
第 3题
P108 第 4题
第 5题
复 习例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习
