平行四边形的判定一
图片预览






文档简介
课件21张PPT。平行四边形的判定(一)知识点回顾定义:有两组对边分别平行的四边形叫做平行四边形.性质:1·两组对边分别相等
2·两组对角分别相等
3·两条对角线互相平分
那么,怎么来判断一个四边形是否是平行四边形呢?
当然,我们可以根据平行四边形的定义加以判定:两组对边分别平行的四边形是平行四边形。
那么是否还存在其他的判定方法呢?
创设情境,引入新课思考 由平行四边形的性质“平行四边形的两组对边分别相等”,逆向思考,互换条件与结论,试写出它的逆命题,你认为它是一个真命题吗?一个四边形是平行四边形
一个四边形的两组对边分别相等
它的两组对边
分别相等这个四边形是平
行四边形猜想:两组对边分别相等的四边形是平行四边形。 探究1:作一个两组对边分别相等的四边形,把你作的四边形和其他同学作的进行比较,看看有什么发现?
发现:尽管大家所作的四边形都不一样,但是,发现,他们都是平行四边形!
猜想:两组对边分别相等的四边形是平行四边形
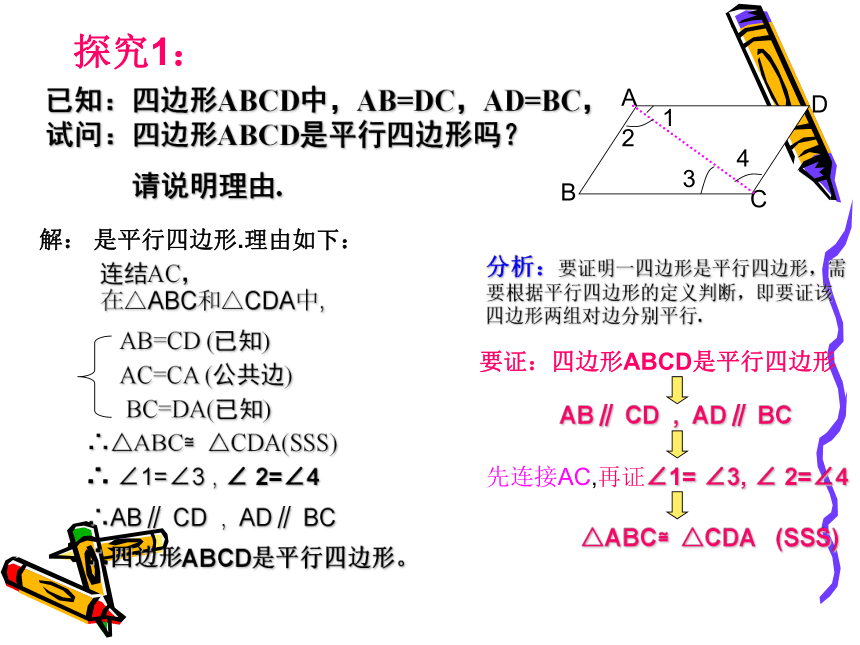
探究1:已知:四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?
请说明理由.分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行.要证:四边形ABCD是平行四边形AB∥ CD , AD∥ BC先连接AC,再证∠1= ∠3, ∠ 2=∠4
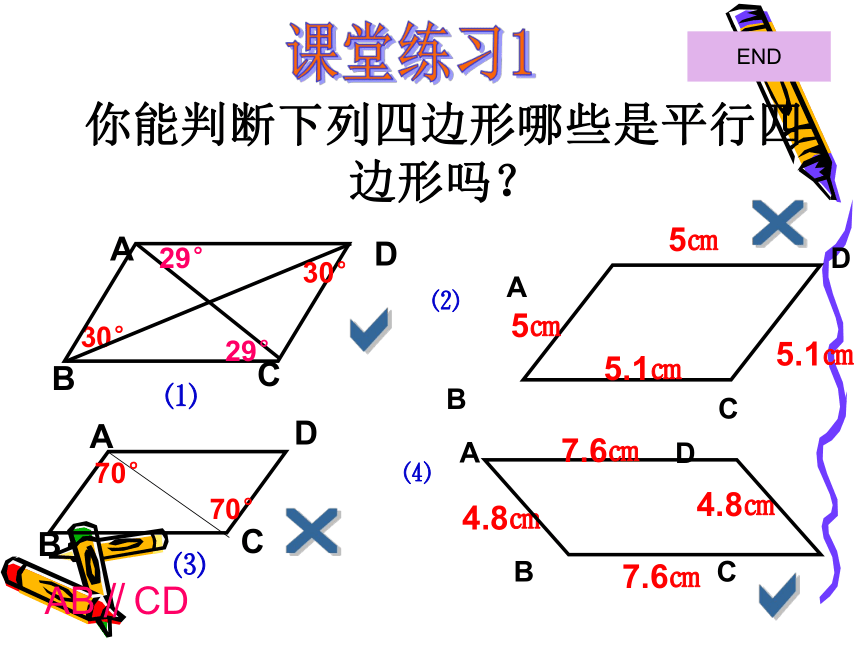
△ABC≌△CDA (SSS)解:是平行四边形.理由如下:连结AC,AB=CD (已知)AC=CA (公共边)BC=DA(已知)∴△ABC≌△CDA(SSS)在△ABC和△CDA中,∴ ∠1=∠3 , ∠ 2=∠4∴AB∥ CD , AD∥ BC∴四边形ABCD是平行四边形。1234由上述证明可以得到平行四边形的判定定理:两组对边分别相等的四边形是平行四边形。几何语言描述判定:你能判断下列四边形哪些是平行四边形吗?⑷
ABCD5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝5.1㎝5.1㎝ADCB30°⑴⑶ABCD30°29°29°70°70°AB∥CDarar课堂练习1END如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?课堂练习2AB ∥ DC∥ EFAD ∥ BCDE ∥ CFEND平行四边形的判定 定义:两组对边分别平行的四边形是
行四边形
判定一:两组对边分别相等的四边形是平 行四边形
还有其它新方法吗?思考如果只知道四边形的一组对边相等,显然这一条件还不足以保证它是一个平行四边形。从边的角度看,把你认为需要再增加的条件填在下面的空框内:这组对边平行+猜想:
一组对边平行且相等的四边形是平行四边形。探究2:试作一个有一组对边平行且相等的四边形,把你作的四边形和其他同学作的进行比较,看看有什么发现?
发现:尽管大家所作的四边形都不一样,但是,发现,他们都是平行四边形!
猜想:一组对边平行且相等的四边形是平行四边形探究2已知:四边形ABCD中,AB=CD, AB∥CD
试问:四边 形ABCD是平行四边形吗?请说明理由.B解:连接ACACD12是平行四边形.理由如下:∵ AB∥ CD∴ ∠BAC=∠ACD在△ABC和△CDA中,AB=CD (已知)∠BAC=∠ACD (已证)AC=CA (公共边)∴△ABC≌△CDA (SAS)∴ ∠1=∠2∴ AD∥ BC又∵ AB∥ CD∴四边形ABCD是平行四边形由上述证明可以得到平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形.几何语言描述判定:“ ”读作“平行且相等”. 例:在?ABCD中,已知M和N分别是AB、DC上的中点,试说明四边形
BMDN也是平行四边形.解:∵四边形ABCD是平行四边形
∴AB∥CD 且 AB=CD ( )
∵ M和N分别是AB、DC上的中点( )
∴ BM∥DN 且 BM=DN
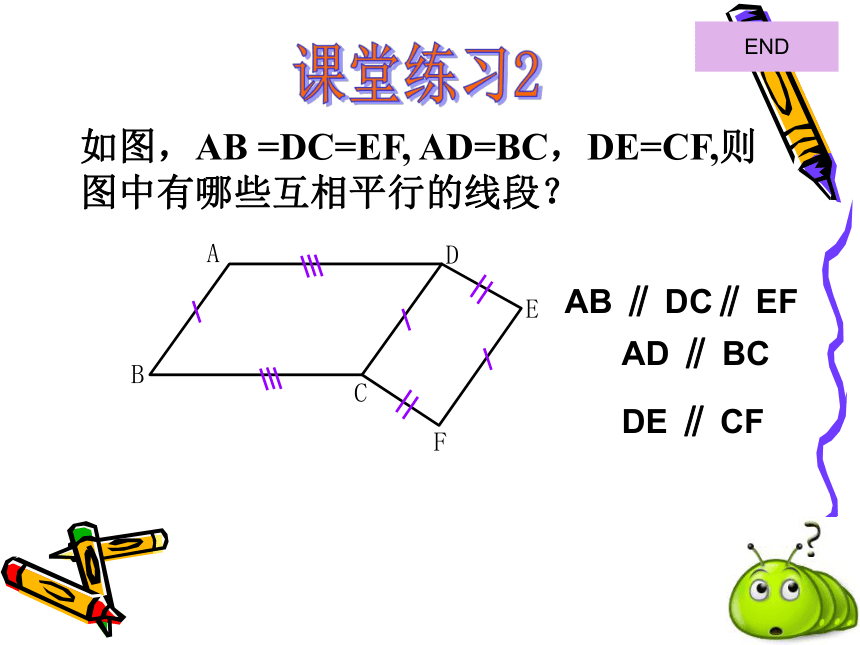
∴四边形BMDN也是平行四边形( )练兵场 1、如图,AC∥ED,点B在AC上且AB=ED=BC .找出图中的平行四边形. ACBED2、如图,在?ABCD中,已知点F和点E分别在AD和BC上,且AF=CE,连结CF和AE,说明四边形AFCE是平行四边形. 要说明四边形AFCE是平行四边形就需:或有一组对边平行且相等两组对边都分别平行或两组对边分别相等 若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?C4、填空题: 如图,在四边形ABCD中,1.如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形.2.如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形.84点评:两组对边相等的四边形是平行四边形6点评:一组对边平行且相等的四边形是平行四边形 判定 1 定义:两组对边分别平行的四边形是平行四边形. 判定2 两组对边分别相等的四边形是平行四边形. 判定3 一组对边平行且相等的四边形是平行四边形.本节 课主要学习了平行四边形的判定定理:教材107页 第 1、3题
《同步三练》第54页第1、2、3、4题
作业布置
2·两组对角分别相等
3·两条对角线互相平分
那么,怎么来判断一个四边形是否是平行四边形呢?
当然,我们可以根据平行四边形的定义加以判定:两组对边分别平行的四边形是平行四边形。
那么是否还存在其他的判定方法呢?
创设情境,引入新课思考 由平行四边形的性质“平行四边形的两组对边分别相等”,逆向思考,互换条件与结论,试写出它的逆命题,你认为它是一个真命题吗?一个四边形是平行四边形
一个四边形的两组对边分别相等
它的两组对边
分别相等这个四边形是平
行四边形猜想:两组对边分别相等的四边形是平行四边形。 探究1:作一个两组对边分别相等的四边形,把你作的四边形和其他同学作的进行比较,看看有什么发现?
发现:尽管大家所作的四边形都不一样,但是,发现,他们都是平行四边形!
猜想:两组对边分别相等的四边形是平行四边形
探究1:已知:四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?
请说明理由.分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行.要证:四边形ABCD是平行四边形AB∥ CD , AD∥ BC先连接AC,再证∠1= ∠3, ∠ 2=∠4
△ABC≌△CDA (SSS)解:是平行四边形.理由如下:连结AC,AB=CD (已知)AC=CA (公共边)BC=DA(已知)∴△ABC≌△CDA(SSS)在△ABC和△CDA中,∴ ∠1=∠3 , ∠ 2=∠4∴AB∥ CD , AD∥ BC∴四边形ABCD是平行四边形。1234由上述证明可以得到平行四边形的判定定理:两组对边分别相等的四边形是平行四边形。几何语言描述判定:你能判断下列四边形哪些是平行四边形吗?⑷
ABCD5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝5.1㎝5.1㎝ADCB30°⑴⑶ABCD30°29°29°70°70°AB∥CDarar课堂练习1END如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?课堂练习2AB ∥ DC∥ EFAD ∥ BCDE ∥ CFEND平行四边形的判定 定义:两组对边分别平行的四边形是
行四边形
判定一:两组对边分别相等的四边形是平 行四边形
还有其它新方法吗?思考如果只知道四边形的一组对边相等,显然这一条件还不足以保证它是一个平行四边形。从边的角度看,把你认为需要再增加的条件填在下面的空框内:这组对边平行+猜想:
一组对边平行且相等的四边形是平行四边形。探究2:试作一个有一组对边平行且相等的四边形,把你作的四边形和其他同学作的进行比较,看看有什么发现?
发现:尽管大家所作的四边形都不一样,但是,发现,他们都是平行四边形!
猜想:一组对边平行且相等的四边形是平行四边形探究2已知:四边形ABCD中,AB=CD, AB∥CD
试问:四边 形ABCD是平行四边形吗?请说明理由.B解:连接ACACD12是平行四边形.理由如下:∵ AB∥ CD∴ ∠BAC=∠ACD在△ABC和△CDA中,AB=CD (已知)∠BAC=∠ACD (已证)AC=CA (公共边)∴△ABC≌△CDA (SAS)∴ ∠1=∠2∴ AD∥ BC又∵ AB∥ CD∴四边形ABCD是平行四边形由上述证明可以得到平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形.几何语言描述判定:“ ”读作“平行且相等”. 例:在?ABCD中,已知M和N分别是AB、DC上的中点,试说明四边形
BMDN也是平行四边形.解:∵四边形ABCD是平行四边形
∴AB∥CD 且 AB=CD ( )
∵ M和N分别是AB、DC上的中点( )
∴ BM∥DN 且 BM=DN
∴四边形BMDN也是平行四边形( )练兵场 1、如图,AC∥ED,点B在AC上且AB=ED=BC .找出图中的平行四边形. ACBED2、如图,在?ABCD中,已知点F和点E分别在AD和BC上,且AF=CE,连结CF和AE,说明四边形AFCE是平行四边形. 要说明四边形AFCE是平行四边形就需:或有一组对边平行且相等两组对边都分别平行或两组对边分别相等 若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?C4、填空题: 如图,在四边形ABCD中,1.如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形.2.如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形.84点评:两组对边相等的四边形是平行四边形6点评:一组对边平行且相等的四边形是平行四边形 判定 1 定义:两组对边分别平行的四边形是平行四边形. 判定2 两组对边分别相等的四边形是平行四边形. 判定3 一组对边平行且相等的四边形是平行四边形.本节 课主要学习了平行四边形的判定定理:教材107页 第 1、3题
《同步三练》第54页第1、2、3、4题
作业布置
