二面角的平面角[下学期]
图片预览


文档简介
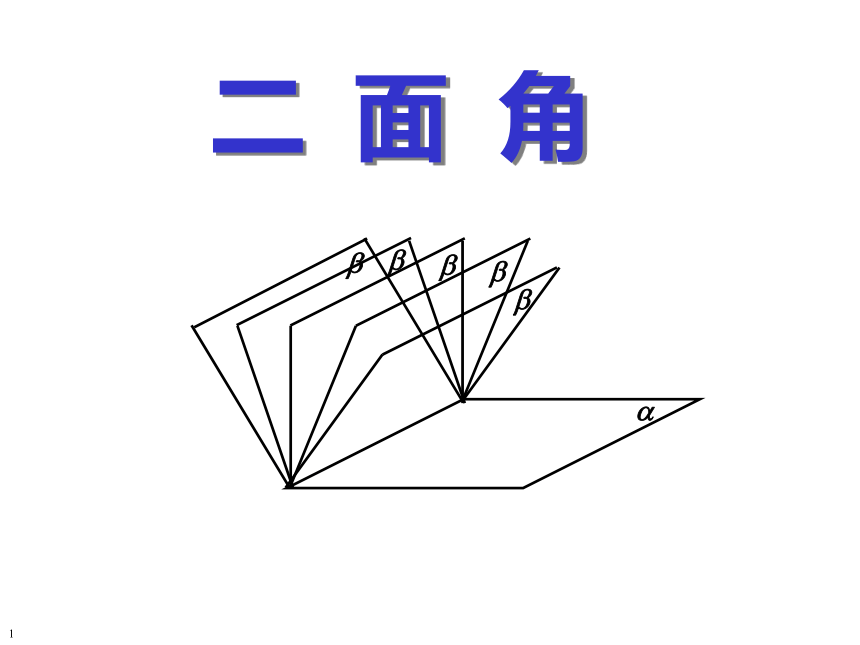
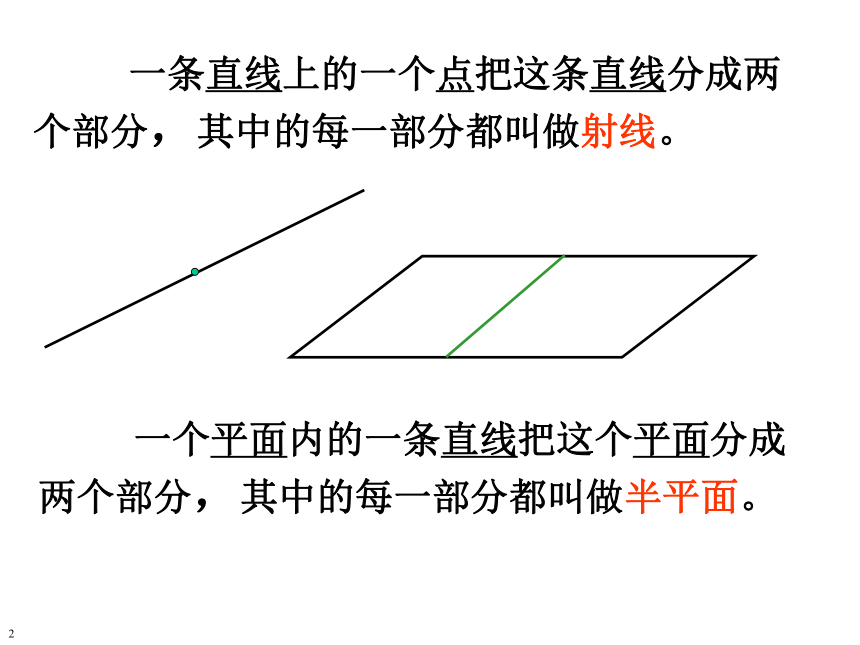
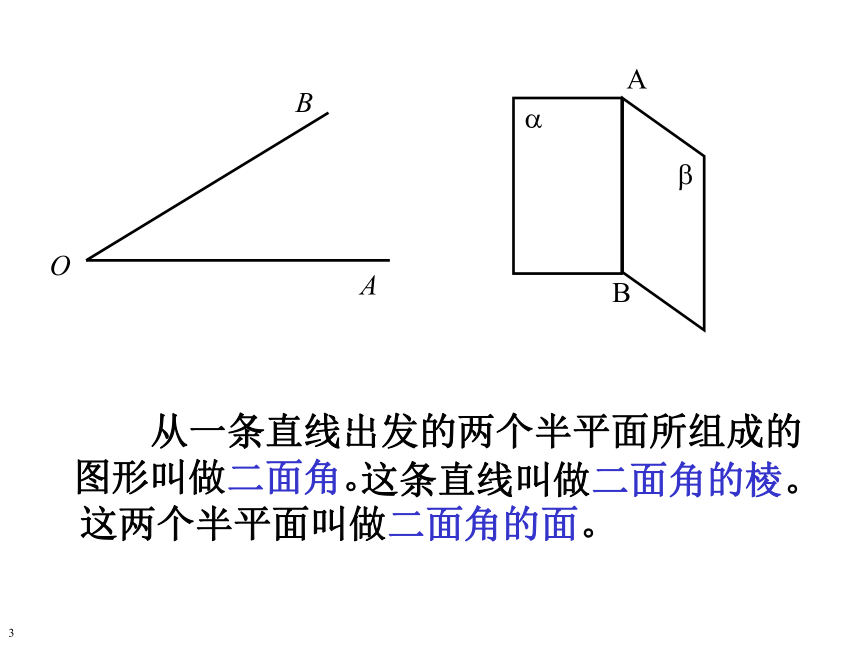
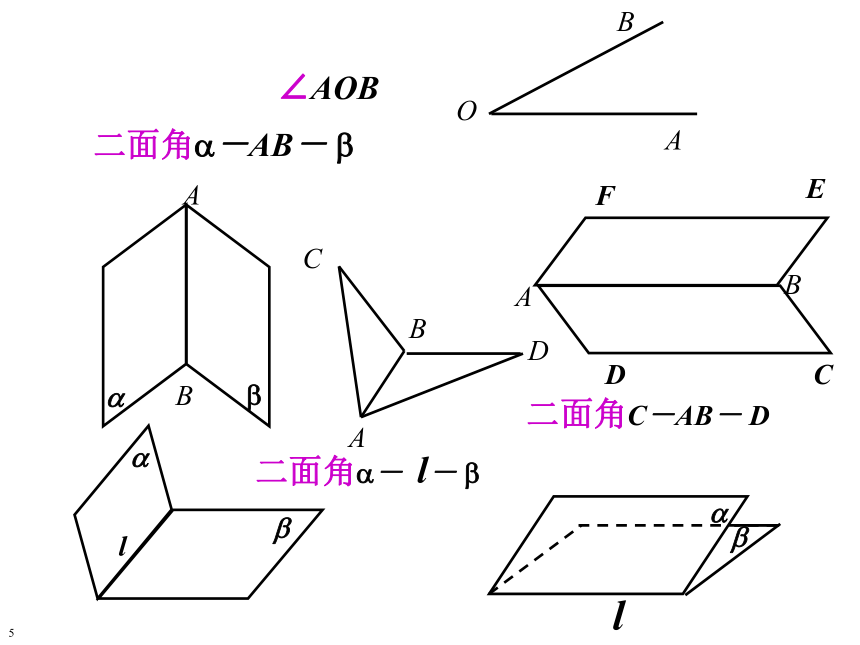
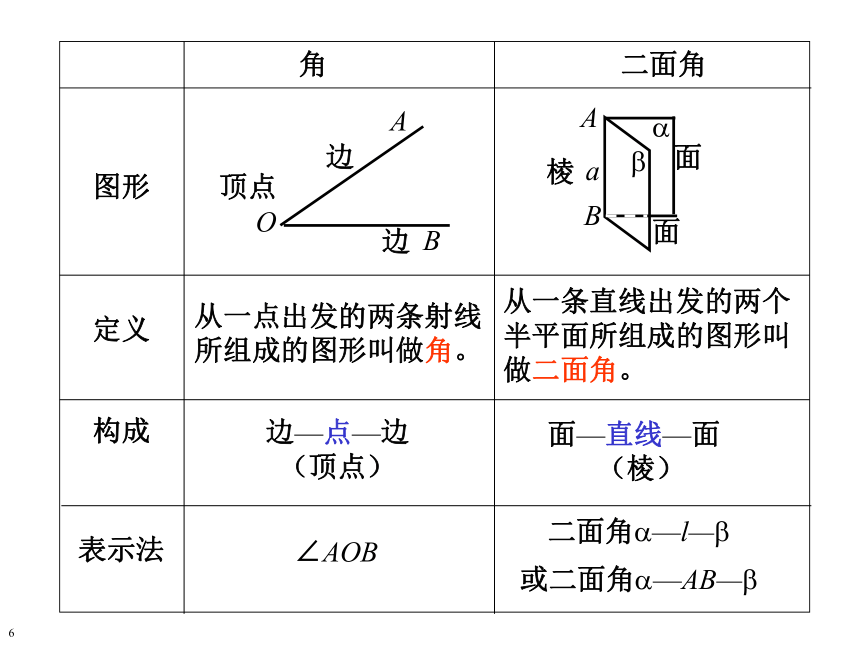
课件19张PPT。二 面 角空间两个平面?二 面 角1 一个平面内的一条直线把这个平面分成两个部分,其中的每一部分都叫做半平面。 一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫做射线。2OBA??AB 从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱。这两个半平面叫做二面角的面。37二面角?-AB- ?二面角?- l- ?二面角C-AB- D5∠AOB角从一点出发的两条射线所组成的图形叫做角。定义构成边—点—边
(顶点)表示法∠AOB图形6ABA1B1∠A O B∠A1O1B1 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。平面角是直角的二面角叫做直二面角9二面角的大小用它的平面角来度量注意:二面角的平面角必须满足: 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。10练习:
指出下列各图中的二面角的平面角:二面角B--B’C--Al二面角?--l--?OEOO二面角A--BC--DD14二面角的平面角的作法:1、定义法
根据定义作出来2、垂面法
作与棱垂直的平面与
两半平面的交线得到123、三垂线定理法
借助三垂线定理或
其逆定理作出来二面角的计算:1、找到或作出二面角的平面角2、证明 1中的角就是所求的角3、计算出此角的大小例1例2一“作”二“证”三“计算”16AOD解:过 A作 AO⊥?于O,过 O作 OD⊥ l 于D,连AD则由三垂线定理得 AD⊥ l∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∵sin∠ADO= ∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在Rt△ADO中,①②③17AOD解:过 A作 AO⊥?于O,过 O作 OD⊥ l 于D,连AD则由三垂线定理得 AD⊥ l∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∵sin∠ADO= ∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在Rt△ADO中,AO
AD18例 2 如图,已知A、B是120?的二面角?—l—?棱l上的两点,线段AC,BD分别在面?,?内,且AC⊥l,BD⊥l ,AC=2,BD=1,AB=3,求线段CD的长。lO19∠OAC =120?AO=BD=1, AC=2四边形ABDO为矩形, DO=AB=3例 2 如图,已知A、B是120?的二面角?—l—?棱l上的两点,线段AC,BD分别在面?,?内,且AC⊥l,BD⊥l ,AC=2,BD=1,AB=3,求线段CD的长。l ∵BD⊥l ∴ AO∥BD,∴四边形ABDO为矩形,
∴ DO∥ l , AO=BD ∵ AC⊥l , AO⊥l ,
∴ l ⊥平面CAO ∴ AO⊥l ∴ CO⊥DO O19E解:在平面?内,过A作AO⊥l ,使
AO=BD, 连结CO、DO, 则∠OAC就是
二面角?—l—?的平面角,即 ∠OAC =120?,二面角B--B’C--A二面角A--BC--D21二面角B--AD--C11设AB=1,则AE=3OE练习:二 面 角一、二面角的定义:二、二面角的表示方法:三、二面角的平面角:四、二面角的平面角的作法:五、二面角的计算:二 面 角 ?-AB- ?
二 面 角 C-AB- D
二 面 角 ?- l- ?1、根据定义作出来
2、利用直线和平面垂
直作出来
3、借助三垂线定理或
其逆定理作出来1、找到或作出二面角的平面角
2、证明 1中的角就是所求的 角
3、计算所求的角一“作”二“证”三“计算”从一条直线出发的两个半
平面所组成的图形叫做二
面角。这条直线叫做二面
角的棱。这两个半平面叫
做二面角的面。 221、二面角的平面角
必须满足三个条件
2、二面角的平面角
的大小与 其顶点
在棱上的位置无关
3、二面角的大小用
它的平面角的大
小来度量 作业1. 课本P.46 4,5,7
2.《苏大》P.176 6
(顶点)表示法∠AOB图形6ABA1B1∠A O B∠A1O1B1 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。平面角是直角的二面角叫做直二面角9二面角的大小用它的平面角来度量注意:二面角的平面角必须满足: 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。10练习:
指出下列各图中的二面角的平面角:二面角B--B’C--Al二面角?--l--?OEOO二面角A--BC--DD14二面角的平面角的作法:1、定义法
根据定义作出来2、垂面法
作与棱垂直的平面与
两半平面的交线得到123、三垂线定理法
借助三垂线定理或
其逆定理作出来二面角的计算:1、找到或作出二面角的平面角2、证明 1中的角就是所求的角3、计算出此角的大小例1例2一“作”二“证”三“计算”16AOD解:过 A作 AO⊥?于O,过 O作 OD⊥ l 于D,连AD则由三垂线定理得 AD⊥ l∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∵sin∠ADO= ∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在Rt△ADO中,①②③17AOD解:过 A作 AO⊥?于O,过 O作 OD⊥ l 于D,连AD则由三垂线定理得 AD⊥ l∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∵sin∠ADO= ∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在Rt△ADO中,AO
AD18例 2 如图,已知A、B是120?的二面角?—l—?棱l上的两点,线段AC,BD分别在面?,?内,且AC⊥l,BD⊥l ,AC=2,BD=1,AB=3,求线段CD的长。lO19∠OAC =120?AO=BD=1, AC=2四边形ABDO为矩形, DO=AB=3例 2 如图,已知A、B是120?的二面角?—l—?棱l上的两点,线段AC,BD分别在面?,?内,且AC⊥l,BD⊥l ,AC=2,BD=1,AB=3,求线段CD的长。l ∵BD⊥l ∴ AO∥BD,∴四边形ABDO为矩形,
∴ DO∥ l , AO=BD ∵ AC⊥l , AO⊥l ,
∴ l ⊥平面CAO ∴ AO⊥l ∴ CO⊥DO O19E解:在平面?内,过A作AO⊥l ,使
AO=BD, 连结CO、DO, 则∠OAC就是
二面角?—l—?的平面角,即 ∠OAC =120?,二面角B--B’C--A二面角A--BC--D21二面角B--AD--C11设AB=1,则AE=3OE练习:二 面 角一、二面角的定义:二、二面角的表示方法:三、二面角的平面角:四、二面角的平面角的作法:五、二面角的计算:二 面 角 ?-AB- ?
二 面 角 C-AB- D
二 面 角 ?- l- ?1、根据定义作出来
2、利用直线和平面垂
直作出来
3、借助三垂线定理或
其逆定理作出来1、找到或作出二面角的平面角
2、证明 1中的角就是所求的 角
3、计算所求的角一“作”二“证”三“计算”从一条直线出发的两个半
平面所组成的图形叫做二
面角。这条直线叫做二面
角的棱。这两个半平面叫
做二面角的面。 221、二面角的平面角
必须满足三个条件
2、二面角的平面角
的大小与 其顶点
在棱上的位置无关
3、二面角的大小用
它的平面角的大
小来度量 作业1. 课本P.46 4,5,7
2.《苏大》P.176 6
