山东济南2023年天桥区九年级中考数学三模考试试题(含答案)
文档属性
| 名称 | 山东济南2023年天桥区九年级中考数学三模考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 500.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:43:22 | ||
图片预览



文档简介
九年级中考数学三模考试试题
满分150分 时间:120分钟
一、单选题。(每小题4分,共40分)
1.﹣2023的绝对值是( )
A.2023 B.﹣ C.﹣2023 D.
2.用3个同样的小正方体摆出的几何体,从三个方向看到的图形如图所示,这个几何体是( )
3.今年某款软件的下载量达到了286 000万次,,其中“286 000”用科学记数法表示为( )
A.286×103 B.28.6×104 C.2.86×105 D.0.286×106
4.如图,直线a∥b,AB⊥AC,∠1=55°,则∠2的度数为( )
A.30° B.35° C.45° D.50°
(第4题图) (第6题图) (第7题图)
5.中国二十四节气已被列为联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大学”,其中既是轴对称图形,但不是中心对称图形的是( )
6.宫商角徽羽是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6),现有一款一起听古音的音乐玩具,音乐小球从A处沿轨道进入小洞就可以发出相应的声音,且小球每次进入每个小洞的可能性大小相同,现有一个音乐小球从A处先两次进入小洞,先发出“商”音,在发出“羽”音的概率是( )
A. B. C. D.
7.如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕点O逆时针方向旋转90°得到△A’B’C’,则点A’的坐标是( )
A.(4,1) B.(4,﹣1) C.(﹣1,4) D.(1,﹣4)
8.如图,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏BC的长为xcm,则下列各方程中,符合题意的是( )
A.x(80-x)=640 B.x(80-2x)=640 C.x(80-2x)=640 D.x(80-x)=640
(第8题图) (第9题图)
9.如图,在矩形ABCD中,AB=2,BC=4,分别以点A和C为圆心,大于AC长为半径作弧,两弧相交于点M和点N,作直线MN分别交AD,BC于点E、F,则AE的长为( )
A.5 B. C. D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W,例如当a=2时,区域W内的整点个数为1,若区域W内恰好有7个整点,则a的取值范围是( )
A.3<a≤4 B.3≤a<4 C.2<a≤3 D.2≤a<3
二.填空题。(每小题4分,共24分)11.分解因式:a2-2ab= .
12.小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率为 .
(第12题图) (第14题图)
13.关于x的方程x2-4x+m=0有一根为﹣1,则另一根为 .
14.如图,正六边形ABCDEF的边长为2,以点A为圆心,AC的长为半径画弧EC,连接AC,AE,则图中阴影部分的面积是 .
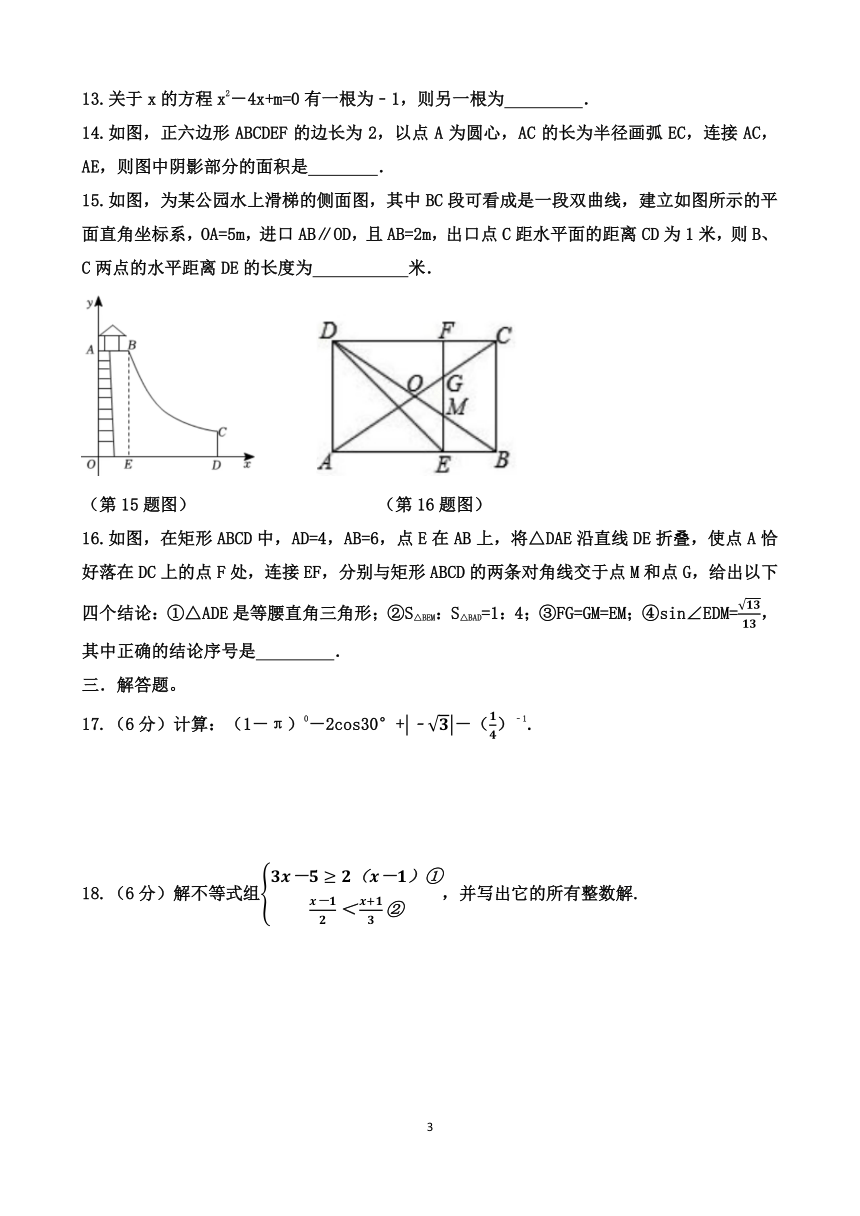
15.如图,为某公园水上滑梯的侧面图,其中BC段可看成是一段双曲线,建立如图所示的平面直角坐标系,OA=5m,进口AB∥OD,且AB=2m,出口点C距水平面的距离CD为1米,则B、C两点的水平距离DE的长度为 米.
(第15题图) (第16题图)
16.如图,在矩形ABCD中,AD=4,AB=6,点E在AB上,将△DAE沿直线DE折叠,使点A恰好落在DC上的点F处,连接EF,分别与矩形ABCD的两条对角线交于点M和点G,给出以下四个结论:①△ADE是等腰直角三角形;②S△BEM:S△BAD=1:4;③FG=GM=EM;④sin∠EDM=,其中正确的结论序号是 .
三.解答题。
17.(6分)计算:(1-π)0-2cos30°+-()﹣1.
18.(6分)解不等式组,并写出它的所有整数解.
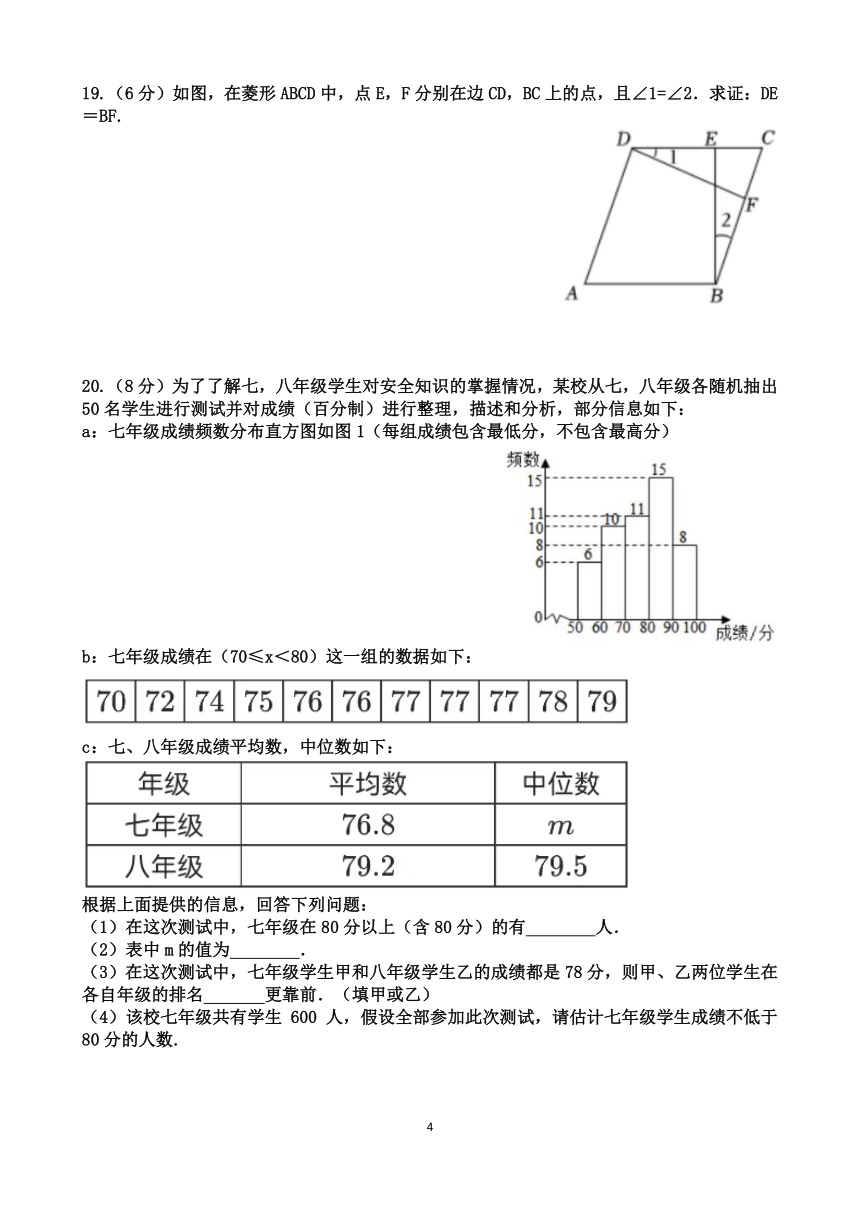
19.(6分)如图,在菱形ABCD中,点E,F分别在边CD,BC上的点,且∠1=∠2.求证:DE=BF.
20.(8分)为了了解七,八年级学生对安全知识的掌握情况,某校从七,八年级各随机抽出50名学生进行测试并对成绩(百分制)进行整理,描述和分析,部分信息如下:
a:七年级成绩频数分布直方图如图1(每组成绩包含最低分,不包含最高分)
b:七年级成绩在(70≤x<80)这一组的数据如下:
c:七、八年级成绩平均数,中位数如下:
根据上面提供的信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人.
(2)表中m的值为 .
(3)在这次测试中,七年级学生甲和八年级学生乙的成绩都是78分,则甲、乙两位学生在各自年级的排名 更靠前.(填甲或乙)
(4)该校七年级共有学生600人,假设全部参加此次测试,请估计七年级学生成绩不低于80分的人数.
21(8分)某中学九年级一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B的仰角为45°,走7米到C处测得B点的仰角为55°,已知O,A,C在同一条直线上.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
(1)求∠ABC的度数.
(2)求新教学楼OB的高度
22.(8分)如图,O的直径AB与其弦CD相交于点E,过点A的切线交CD的延长线于点F,且∠AED=∠EAD.
(1)求证:AD=DF;
(2)若AE=6,sin∠AFE=,求O的半径长.
23.(10分)某商场在世界杯开始之前,用6000元共购进A,B两种世界杯吉祥物110个,用于购买A种吉祥物与购买B种吉祥物的费用相同,且A种吉祥物的单价是B种吉祥物的1.2倍.
(1)求A,B两种吉祥物的单价分别是多少元;
(2)商场计划用不超过16800元的资金再次购进A,B两种吉祥物共300个,已知A,B两种吉祥物的进件不变,求A种吉祥物最多能购进多少个?
24.(10分)如图,矩形OABC的顶点O为坐标原点,点C在x轴的正半轴上,点A在y轴的正半轴上,OA=6,OC=2,反比例函数y=的图象经过AB的中点D,且与BC交于点E.
(1)求K的值和点E的坐标;
(2)连接DO,DE,求四边形DOCE的面积;
(3)M为x轴上一点,N为反比例函数y=的图象上一点,是否存在以点M,N,D,E为顶点的四边形是平行四边形,若存在直接写出M,N两点的坐标,若不存在,说明理由.
25.(12分)如图,在Rt△ABC中,∠ACB=90°,∠ABC=45°,点D为直线AC上的任意一点,过点D作DE∥BC交直线AB于点E,过点A作AF⊥BD,交直线BD于点F,垂足为点F,直线AF与直线BC交于点G.
(1)如图1,当点D在边AC上时,则线段DE,CG,BC之间的数量关系是 .
(2)如图2,当点D在边AC的延长线上时,则线段DE,CG,BC之间的数量关系是 ,请证明你的结论.
(3)如图3,在(2)的条件下,若CD=6,DE=10,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段DE于点M、N,当DM=2时,求线段EN的长.
(图1) (图2) (图3)
26.(12分)如图,抛物线y=ax2+x+c与x轴交于A(﹣4,0)和B,与y轴交于点C(0,6),直线l经过B,C两点.
(1)求抛物线的解析式;
(2)点D是直线l上方抛物线上一点,其横坐标为m,过点D作直线DE⊥x轴于点E,交直线l于点F,当DF=2EF时,求点D的坐标;
(3)在(2)的条件下,在y轴上是否存在点P,使得∠PAB=2∠DAB?若存在,请直接写出点P的坐标,若不存在,说明理由.
备用图
答案解析
一.单选题。(每小题4分,共40分)
1.﹣2023的绝对值是( A )
A.2023 B.﹣ C.﹣2023 D.
2.用3个同样的小正方体摆出的几何体,从三个方向看到的图形如图所示,这个几何体是( B )
3.今年某款软件的下载量达到了286 000万次,,其中“286 000”用科学记数法表示为( C )
A.286×103 B.28.6×104 C.2.86×105 D.0.286×106
4.如图,直线a∥b,AB⊥AC,∠1=55°,则∠2的度数为( B )
A.30° B.35° C.45° D.50°
(第4题图) (第6题图) (第7题图)
5.中国二十四节气已被列为联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大学”,其中既是轴对称图形,但不是中心对称图形的是( D )
6.宫商角徽羽是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6),现有一款一起听古音的音乐玩具,音乐小球从A处沿轨道进入小洞就可以发出相应的声音,且小球每次进入每个小洞的可能性大小相同,现有一个音乐小球从A处先两次进入小洞,先发出“商”音,在发出“羽”音的概率是( D )
A. B. C. D.
7.如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕点O逆时针方向旋转90°得到△A’B’C’,则点A’的坐标是( D )
A.(4,1) B.(4,﹣1) C.(﹣1,4) D.(1,﹣4)
8.如图,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏BC的长为xcm,则下列各方程中,符合题意的是( A )
A.x(80-x)=640 B.x(80-2x)=640 C.x(80-2x)=640 D.x(80-x)=640
(第8题图) (第9题图)
9.如图,在矩形ABCD中,AB=2,BC=4,分别以点A和C为圆心,大于AC长为半径作弧,两弧相交于点M和点N,作直线MN分别交AD,BC于点E、F,则AE的长为( C )
A.5 B. C. D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W,例如当a=2时,区域W内的整点个数为1,若区域W内恰好有7个整点,则a的取值范围是( A )
A.3<a≤4 B.3≤a<4 C.2<a≤3 D.2≤a<3
二.填空题。(每小题4分,共24分)11.分解因式:a2-2ab= a(a-2b) .
12.小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率为 .
(第12题图) (第14题图)
13.关于x的方程x2-4x+m=0有一根为﹣1,则另一根为 x=5 .
14.如图,正六边形ABCDEF的边长为2,以点A为圆心,AC的长为半径画弧EC,连接AC,AE,则图中阴影部分的面积是 2π .
15.如图,为某公园水上滑梯的侧面图,其中BC段可看成是一段双曲线,建立如图所示的平面直角坐标系,OA=5m,进口AB∥OD,且AB=2m,出口点C距水平面的距离CD为1米,则B、C两点的水平距离DE的长度为 8 米.
(第15题图) (第16题图)
16.如图,在矩形ABCD中,AD=4,AB=6,点E在AB上,将△DAE沿直线DE折叠,使点A恰好落在DC上的点F处,连接EF,分别与矩形ABCD的两条对角线交于点M和点G,给出以下四个结论:①△ADE是等腰直角三角形;②S△BEM:S△BAD=1:4;③FG=GM=EM;④sin∠EDM=,其中正确的结论序号是 ①③ .
三.解答题。
17.(6分)计算:(1-π)0-2cos30°+-()﹣1.
=1-+-4
=﹣3
18.(6分)解不等式组,并写出它的所有整数解.
解不等式①得x≥3
解不等式②得x<5
不等式组解集为3≤x<5
不等式组解集为3,4
19.(6分)如图,在菱形ABCD中,点E,F分别在边CD,BC上的点,且∠1=∠2.求证:DE=BF.
证明:∵四边形ABCD是菱形
∴CB=CD
∵∠1=∠2,∠C=∠C
∴△CDF≌△CBE
∴DE=BF
20.(8分)为了了解七,八年级学生对安全知识的掌握情况,某校从七,八年级各随机抽出50名学生进行测试并对成绩(百分制)进行整理,描述和分析,部分信息如下:
a:七年级成绩频数分布直方图如图1(每组成绩包含最低分,不包含最高分)
b:七年级成绩在(70≤x<80)这一组的数据如下:
c:七、八年级成绩平均数,中位数如下:
根据上面提供的信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人.
(2)表中m的值为 .
(3)在这次测试中,七年级学生甲和八年级学生乙的成绩都是78分,则甲、乙两位学生在各自年级的排名 更靠前.(填甲或乙)
(4)该校七年级共有学生600人,假设全部参加此次测试,请估计七年级学生成绩不低于80分的人数.
(1)15+8=23人
(2)m=(77+78)÷2=77.5分
(3)甲
(4)600×=276人
答:276人
21(8分)某中学九年级一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B的仰角为45°,走7米到C处测得B点的仰角为55°,已知O,A,C在同一条直线上.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
(1)求∠ABC的度数.
(2)求新教学楼OB的高度
(1)∵∠BOC是△ABC的外角
∴∠ABC=∠BCO-∠A=55°-45°=10°
(2)在Rt△AOB中,∠A=45°
∴OA=OB
∵AC=7m
∴OC=OB-7
在Rt△COB中,∠BCO=55°
∴tan∠BCO=
∴=1.43
即OB≈23.3
答:高度约23.3米
22.(8分)如图,O的直径AB与其弦CD相交于点E,过点A的切线交CD的延长线于点F,且∠AED=∠EAD.
(1)求证:AD=DF;
(2)若AE=6,sin∠AFE=,求O的半径长.
(1)证明:∵AF与O相切,
∴AB⊥AF
∴∠FAD+∠EAD=90°
∵∠AED=∠EAD
∴∠F=∠FAD
∴AD=FD
(2)∵∠EAF=90°
∴cos∠AEF==
∵AE=6
∴EF=10
∵∠AED=∠EAD
∴AD=ED
∴AD=EF=5
cos∠EAD=cos∠AEF=
即=
∴AB=
∴O的半径为
23.(10分)某商场在世界杯开始之前,用6000元共购进A,B两种世界杯吉祥物110个,用于购买A种吉祥物与购买B种吉祥物的费用相同,且A种吉祥物的单价是B种吉祥物的1.2倍.
(1)求A,B两种吉祥物的单价分别是多少元;
(2)商场计划用不超过16800元的资金再次购进A,B两种吉祥物共300个,已知A,B两种吉祥物的进件不变,求A种吉祥物最多能购进多少个?
(1)解设:B种吉祥物单价为x元,则A种吉祥物单价为1.2x元。
+=110
x=50
经检验,x=50是原方程的根
50×1.2=60元
答:A种吉祥物单价为60元,B种吉祥物单价为50元.
(2)购买a个A吉祥物,则B种吉祥物为(300-a)个.
60a+50(300-a)≤16800
a≤180
A种吉祥物最多购进180个.
24.(10分)如图,矩形OABC的顶点O为坐标原点,点C在x轴的正半轴上,点A在y轴的正半轴上,OA=6,OC=2,反比例函数y=的图象经过AB的中点D,且与BC交于点E.
(1)求K的值和点E的坐标;
(2)连接DO,DE,求四边形DOCE的面积;
(3)M为x轴上一点,N为反比例函数y=的图象上一点,是否存在以点M,N,D,E为顶点的四边形是平行四边形,若存在直接写出M,N两点的坐标,若不存在,说明理由.
(1)在矩形OABC中,OA=6,OC=2
∴E点横坐标为2,D点的纵坐标为6.
∵点D为AB的中点
∴点D(1,6)
将D(1,6)代入y=得
k=1×6=6
将E点横坐标为2代入y=
y==3
∴点E(2,3)
(2)四边形DOCE的面积为6×2-6×1×-3×1×=7.5
(3)存在
M(﹣3,0),N(﹣2,﹣3)或M(,0),N(,9)
25.(12分)如图,在Rt△ABC中,∠ACB=90°,∠ABC=45°,点D为直线AC上的任意一点,过点D作DE∥BC交直线AB于点E,过点A作AF⊥BD,交直线BD于点F,垂足为点F,直线AF与直线BC交于点G.
(1)如图1,当点D在边AC上时,则线段DE,CG,BC之间的数量关系是 .
(2)如图2,当点D在边AC的延长线上时,则线段DE,CG,BC之间的数量关系是 ,请证明你的结论.
(3)如图3,在(2)的条件下,若CD=6,DE=10,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段DE于点M、N,当DM=2时,求线段EN的长.
(图1) (图2) (图3)
(1)BC=DE+CG
(2)DE=CG+BC
理由如下:过点B作BP⊥ED
则四边形BPDC为矩形,
∴BC=PD
在Rt△ABC中,∠ACB=90°,∠ABC=45° ED∥BC
∴△ABC和△AED都为等腰直角三角形
∴AC=BC AD=DE
∵AG⊥BD
∴∠BFG=90°
∵∠GBF=∠CBD
∴∠CAG=∠CBD ∠ACB=90°
在△ADC和△BDF
∴△ADC≌△BDF
∴CG=CD
∴DE=CG+BC
(3)EN=3
26.(12分)如图,抛物线y=ax2+x+c与x轴交于A(﹣4,0)和B,与y轴交于点C(0,6),直线l经过B,C两点.
(1)求抛物线的解析式;
(2)点D是直线l上方抛物线上一点,其横坐标为m,过点D作直线DE⊥x轴于点E,交直线l于点F,当DF=2EF时,求点D的坐标;
(3)在(2)的条件下,在y轴上是否存在点P,使得∠PAB=2∠DAB?若存在,请直接写出点P的坐标,若不存在,说明理由.
备用图
(1)将A(﹣4,0),C(0,6)代入y=ax2+x+c得
解得
∴y=﹣x2+x+6
(2)y=0代入y=x2+x+6得
﹣x2+x+6=0
解得x1=﹣4,x2=12
将C(0,6)和B(12,0)代入y=kx+b
解得
∴y=﹣m+6
∵DE⊥x轴,D横坐标为m
∴E(m,0) D(m,﹣m2+m+6) F(m,﹣m+6)
∴EF=﹣m+6 DE=﹣m2+m
∵DF=2EF
∴﹣m2+m=2(﹣m+6)
m1=8,m2=12(舍去)
∴D(8,6)
(3)P(0,)或(0,﹣)
满分150分 时间:120分钟
一、单选题。(每小题4分,共40分)
1.﹣2023的绝对值是( )
A.2023 B.﹣ C.﹣2023 D.
2.用3个同样的小正方体摆出的几何体,从三个方向看到的图形如图所示,这个几何体是( )
3.今年某款软件的下载量达到了286 000万次,,其中“286 000”用科学记数法表示为( )
A.286×103 B.28.6×104 C.2.86×105 D.0.286×106
4.如图,直线a∥b,AB⊥AC,∠1=55°,则∠2的度数为( )
A.30° B.35° C.45° D.50°
(第4题图) (第6题图) (第7题图)
5.中国二十四节气已被列为联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大学”,其中既是轴对称图形,但不是中心对称图形的是( )
6.宫商角徽羽是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6),现有一款一起听古音的音乐玩具,音乐小球从A处沿轨道进入小洞就可以发出相应的声音,且小球每次进入每个小洞的可能性大小相同,现有一个音乐小球从A处先两次进入小洞,先发出“商”音,在发出“羽”音的概率是( )
A. B. C. D.
7.如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕点O逆时针方向旋转90°得到△A’B’C’,则点A’的坐标是( )
A.(4,1) B.(4,﹣1) C.(﹣1,4) D.(1,﹣4)
8.如图,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏BC的长为xcm,则下列各方程中,符合题意的是( )
A.x(80-x)=640 B.x(80-2x)=640 C.x(80-2x)=640 D.x(80-x)=640
(第8题图) (第9题图)
9.如图,在矩形ABCD中,AB=2,BC=4,分别以点A和C为圆心,大于AC长为半径作弧,两弧相交于点M和点N,作直线MN分别交AD,BC于点E、F,则AE的长为( )
A.5 B. C. D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W,例如当a=2时,区域W内的整点个数为1,若区域W内恰好有7个整点,则a的取值范围是( )
A.3<a≤4 B.3≤a<4 C.2<a≤3 D.2≤a<3
二.填空题。(每小题4分,共24分)11.分解因式:a2-2ab= .
12.小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率为 .
(第12题图) (第14题图)
13.关于x的方程x2-4x+m=0有一根为﹣1,则另一根为 .
14.如图,正六边形ABCDEF的边长为2,以点A为圆心,AC的长为半径画弧EC,连接AC,AE,则图中阴影部分的面积是 .
15.如图,为某公园水上滑梯的侧面图,其中BC段可看成是一段双曲线,建立如图所示的平面直角坐标系,OA=5m,进口AB∥OD,且AB=2m,出口点C距水平面的距离CD为1米,则B、C两点的水平距离DE的长度为 米.
(第15题图) (第16题图)
16.如图,在矩形ABCD中,AD=4,AB=6,点E在AB上,将△DAE沿直线DE折叠,使点A恰好落在DC上的点F处,连接EF,分别与矩形ABCD的两条对角线交于点M和点G,给出以下四个结论:①△ADE是等腰直角三角形;②S△BEM:S△BAD=1:4;③FG=GM=EM;④sin∠EDM=,其中正确的结论序号是 .
三.解答题。
17.(6分)计算:(1-π)0-2cos30°+-()﹣1.
18.(6分)解不等式组,并写出它的所有整数解.
19.(6分)如图,在菱形ABCD中,点E,F分别在边CD,BC上的点,且∠1=∠2.求证:DE=BF.
20.(8分)为了了解七,八年级学生对安全知识的掌握情况,某校从七,八年级各随机抽出50名学生进行测试并对成绩(百分制)进行整理,描述和分析,部分信息如下:
a:七年级成绩频数分布直方图如图1(每组成绩包含最低分,不包含最高分)
b:七年级成绩在(70≤x<80)这一组的数据如下:
c:七、八年级成绩平均数,中位数如下:
根据上面提供的信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人.
(2)表中m的值为 .
(3)在这次测试中,七年级学生甲和八年级学生乙的成绩都是78分,则甲、乙两位学生在各自年级的排名 更靠前.(填甲或乙)
(4)该校七年级共有学生600人,假设全部参加此次测试,请估计七年级学生成绩不低于80分的人数.
21(8分)某中学九年级一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B的仰角为45°,走7米到C处测得B点的仰角为55°,已知O,A,C在同一条直线上.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
(1)求∠ABC的度数.
(2)求新教学楼OB的高度
22.(8分)如图,O的直径AB与其弦CD相交于点E,过点A的切线交CD的延长线于点F,且∠AED=∠EAD.
(1)求证:AD=DF;
(2)若AE=6,sin∠AFE=,求O的半径长.
23.(10分)某商场在世界杯开始之前,用6000元共购进A,B两种世界杯吉祥物110个,用于购买A种吉祥物与购买B种吉祥物的费用相同,且A种吉祥物的单价是B种吉祥物的1.2倍.
(1)求A,B两种吉祥物的单价分别是多少元;
(2)商场计划用不超过16800元的资金再次购进A,B两种吉祥物共300个,已知A,B两种吉祥物的进件不变,求A种吉祥物最多能购进多少个?
24.(10分)如图,矩形OABC的顶点O为坐标原点,点C在x轴的正半轴上,点A在y轴的正半轴上,OA=6,OC=2,反比例函数y=的图象经过AB的中点D,且与BC交于点E.
(1)求K的值和点E的坐标;
(2)连接DO,DE,求四边形DOCE的面积;
(3)M为x轴上一点,N为反比例函数y=的图象上一点,是否存在以点M,N,D,E为顶点的四边形是平行四边形,若存在直接写出M,N两点的坐标,若不存在,说明理由.
25.(12分)如图,在Rt△ABC中,∠ACB=90°,∠ABC=45°,点D为直线AC上的任意一点,过点D作DE∥BC交直线AB于点E,过点A作AF⊥BD,交直线BD于点F,垂足为点F,直线AF与直线BC交于点G.
(1)如图1,当点D在边AC上时,则线段DE,CG,BC之间的数量关系是 .
(2)如图2,当点D在边AC的延长线上时,则线段DE,CG,BC之间的数量关系是 ,请证明你的结论.
(3)如图3,在(2)的条件下,若CD=6,DE=10,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段DE于点M、N,当DM=2时,求线段EN的长.
(图1) (图2) (图3)
26.(12分)如图,抛物线y=ax2+x+c与x轴交于A(﹣4,0)和B,与y轴交于点C(0,6),直线l经过B,C两点.
(1)求抛物线的解析式;
(2)点D是直线l上方抛物线上一点,其横坐标为m,过点D作直线DE⊥x轴于点E,交直线l于点F,当DF=2EF时,求点D的坐标;
(3)在(2)的条件下,在y轴上是否存在点P,使得∠PAB=2∠DAB?若存在,请直接写出点P的坐标,若不存在,说明理由.
备用图
答案解析
一.单选题。(每小题4分,共40分)
1.﹣2023的绝对值是( A )
A.2023 B.﹣ C.﹣2023 D.
2.用3个同样的小正方体摆出的几何体,从三个方向看到的图形如图所示,这个几何体是( B )
3.今年某款软件的下载量达到了286 000万次,,其中“286 000”用科学记数法表示为( C )
A.286×103 B.28.6×104 C.2.86×105 D.0.286×106
4.如图,直线a∥b,AB⊥AC,∠1=55°,则∠2的度数为( B )
A.30° B.35° C.45° D.50°
(第4题图) (第6题图) (第7题图)
5.中国二十四节气已被列为联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大学”,其中既是轴对称图形,但不是中心对称图形的是( D )
6.宫商角徽羽是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6),现有一款一起听古音的音乐玩具,音乐小球从A处沿轨道进入小洞就可以发出相应的声音,且小球每次进入每个小洞的可能性大小相同,现有一个音乐小球从A处先两次进入小洞,先发出“商”音,在发出“羽”音的概率是( D )
A. B. C. D.
7.如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕点O逆时针方向旋转90°得到△A’B’C’,则点A’的坐标是( D )
A.(4,1) B.(4,﹣1) C.(﹣1,4) D.(1,﹣4)
8.如图,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏BC的长为xcm,则下列各方程中,符合题意的是( A )
A.x(80-x)=640 B.x(80-2x)=640 C.x(80-2x)=640 D.x(80-x)=640
(第8题图) (第9题图)
9.如图,在矩形ABCD中,AB=2,BC=4,分别以点A和C为圆心,大于AC长为半径作弧,两弧相交于点M和点N,作直线MN分别交AD,BC于点E、F,则AE的长为( C )
A.5 B. C. D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W,例如当a=2时,区域W内的整点个数为1,若区域W内恰好有7个整点,则a的取值范围是( A )
A.3<a≤4 B.3≤a<4 C.2<a≤3 D.2≤a<3
二.填空题。(每小题4分,共24分)11.分解因式:a2-2ab= a(a-2b) .
12.小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率为 .
(第12题图) (第14题图)
13.关于x的方程x2-4x+m=0有一根为﹣1,则另一根为 x=5 .
14.如图,正六边形ABCDEF的边长为2,以点A为圆心,AC的长为半径画弧EC,连接AC,AE,则图中阴影部分的面积是 2π .
15.如图,为某公园水上滑梯的侧面图,其中BC段可看成是一段双曲线,建立如图所示的平面直角坐标系,OA=5m,进口AB∥OD,且AB=2m,出口点C距水平面的距离CD为1米,则B、C两点的水平距离DE的长度为 8 米.
(第15题图) (第16题图)
16.如图,在矩形ABCD中,AD=4,AB=6,点E在AB上,将△DAE沿直线DE折叠,使点A恰好落在DC上的点F处,连接EF,分别与矩形ABCD的两条对角线交于点M和点G,给出以下四个结论:①△ADE是等腰直角三角形;②S△BEM:S△BAD=1:4;③FG=GM=EM;④sin∠EDM=,其中正确的结论序号是 ①③ .
三.解答题。
17.(6分)计算:(1-π)0-2cos30°+-()﹣1.
=1-+-4
=﹣3
18.(6分)解不等式组,并写出它的所有整数解.
解不等式①得x≥3
解不等式②得x<5
不等式组解集为3≤x<5
不等式组解集为3,4
19.(6分)如图,在菱形ABCD中,点E,F分别在边CD,BC上的点,且∠1=∠2.求证:DE=BF.
证明:∵四边形ABCD是菱形
∴CB=CD
∵∠1=∠2,∠C=∠C
∴△CDF≌△CBE
∴DE=BF
20.(8分)为了了解七,八年级学生对安全知识的掌握情况,某校从七,八年级各随机抽出50名学生进行测试并对成绩(百分制)进行整理,描述和分析,部分信息如下:
a:七年级成绩频数分布直方图如图1(每组成绩包含最低分,不包含最高分)
b:七年级成绩在(70≤x<80)这一组的数据如下:
c:七、八年级成绩平均数,中位数如下:
根据上面提供的信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人.
(2)表中m的值为 .
(3)在这次测试中,七年级学生甲和八年级学生乙的成绩都是78分,则甲、乙两位学生在各自年级的排名 更靠前.(填甲或乙)
(4)该校七年级共有学生600人,假设全部参加此次测试,请估计七年级学生成绩不低于80分的人数.
(1)15+8=23人
(2)m=(77+78)÷2=77.5分
(3)甲
(4)600×=276人
答:276人
21(8分)某中学九年级一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B的仰角为45°,走7米到C处测得B点的仰角为55°,已知O,A,C在同一条直线上.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
(1)求∠ABC的度数.
(2)求新教学楼OB的高度
(1)∵∠BOC是△ABC的外角
∴∠ABC=∠BCO-∠A=55°-45°=10°
(2)在Rt△AOB中,∠A=45°
∴OA=OB
∵AC=7m
∴OC=OB-7
在Rt△COB中,∠BCO=55°
∴tan∠BCO=
∴=1.43
即OB≈23.3
答:高度约23.3米
22.(8分)如图,O的直径AB与其弦CD相交于点E,过点A的切线交CD的延长线于点F,且∠AED=∠EAD.
(1)求证:AD=DF;
(2)若AE=6,sin∠AFE=,求O的半径长.
(1)证明:∵AF与O相切,
∴AB⊥AF
∴∠FAD+∠EAD=90°
∵∠AED=∠EAD
∴∠F=∠FAD
∴AD=FD
(2)∵∠EAF=90°
∴cos∠AEF==
∵AE=6
∴EF=10
∵∠AED=∠EAD
∴AD=ED
∴AD=EF=5
cos∠EAD=cos∠AEF=
即=
∴AB=
∴O的半径为
23.(10分)某商场在世界杯开始之前,用6000元共购进A,B两种世界杯吉祥物110个,用于购买A种吉祥物与购买B种吉祥物的费用相同,且A种吉祥物的单价是B种吉祥物的1.2倍.
(1)求A,B两种吉祥物的单价分别是多少元;
(2)商场计划用不超过16800元的资金再次购进A,B两种吉祥物共300个,已知A,B两种吉祥物的进件不变,求A种吉祥物最多能购进多少个?
(1)解设:B种吉祥物单价为x元,则A种吉祥物单价为1.2x元。
+=110
x=50
经检验,x=50是原方程的根
50×1.2=60元
答:A种吉祥物单价为60元,B种吉祥物单价为50元.
(2)购买a个A吉祥物,则B种吉祥物为(300-a)个.
60a+50(300-a)≤16800
a≤180
A种吉祥物最多购进180个.
24.(10分)如图,矩形OABC的顶点O为坐标原点,点C在x轴的正半轴上,点A在y轴的正半轴上,OA=6,OC=2,反比例函数y=的图象经过AB的中点D,且与BC交于点E.
(1)求K的值和点E的坐标;
(2)连接DO,DE,求四边形DOCE的面积;
(3)M为x轴上一点,N为反比例函数y=的图象上一点,是否存在以点M,N,D,E为顶点的四边形是平行四边形,若存在直接写出M,N两点的坐标,若不存在,说明理由.
(1)在矩形OABC中,OA=6,OC=2
∴E点横坐标为2,D点的纵坐标为6.
∵点D为AB的中点
∴点D(1,6)
将D(1,6)代入y=得
k=1×6=6
将E点横坐标为2代入y=
y==3
∴点E(2,3)
(2)四边形DOCE的面积为6×2-6×1×-3×1×=7.5
(3)存在
M(﹣3,0),N(﹣2,﹣3)或M(,0),N(,9)
25.(12分)如图,在Rt△ABC中,∠ACB=90°,∠ABC=45°,点D为直线AC上的任意一点,过点D作DE∥BC交直线AB于点E,过点A作AF⊥BD,交直线BD于点F,垂足为点F,直线AF与直线BC交于点G.
(1)如图1,当点D在边AC上时,则线段DE,CG,BC之间的数量关系是 .
(2)如图2,当点D在边AC的延长线上时,则线段DE,CG,BC之间的数量关系是 ,请证明你的结论.
(3)如图3,在(2)的条件下,若CD=6,DE=10,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段DE于点M、N,当DM=2时,求线段EN的长.
(图1) (图2) (图3)
(1)BC=DE+CG
(2)DE=CG+BC
理由如下:过点B作BP⊥ED
则四边形BPDC为矩形,
∴BC=PD
在Rt△ABC中,∠ACB=90°,∠ABC=45° ED∥BC
∴△ABC和△AED都为等腰直角三角形
∴AC=BC AD=DE
∵AG⊥BD
∴∠BFG=90°
∵∠GBF=∠CBD
∴∠CAG=∠CBD ∠ACB=90°
在△ADC和△BDF
∴△ADC≌△BDF
∴CG=CD
∴DE=CG+BC
(3)EN=3
26.(12分)如图,抛物线y=ax2+x+c与x轴交于A(﹣4,0)和B,与y轴交于点C(0,6),直线l经过B,C两点.
(1)求抛物线的解析式;
(2)点D是直线l上方抛物线上一点,其横坐标为m,过点D作直线DE⊥x轴于点E,交直线l于点F,当DF=2EF时,求点D的坐标;
(3)在(2)的条件下,在y轴上是否存在点P,使得∠PAB=2∠DAB?若存在,请直接写出点P的坐标,若不存在,说明理由.
备用图
(1)将A(﹣4,0),C(0,6)代入y=ax2+x+c得
解得
∴y=﹣x2+x+6
(2)y=0代入y=x2+x+6得
﹣x2+x+6=0
解得x1=﹣4,x2=12
将C(0,6)和B(12,0)代入y=kx+b
解得
∴y=﹣m+6
∵DE⊥x轴,D横坐标为m
∴E(m,0) D(m,﹣m2+m+6) F(m,﹣m+6)
∴EF=﹣m+6 DE=﹣m2+m
∵DF=2EF
∴﹣m2+m=2(﹣m+6)
m1=8,m2=12(舍去)
∴D(8,6)
(3)P(0,)或(0,﹣)
同课章节目录
