2023年中考数学冲刺训练——二次函数解答题1(无答案)
文档属性
| 名称 | 2023年中考数学冲刺训练——二次函数解答题1(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 185.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:45:17 | ||
图片预览



文档简介
2023中考数学冲刺训练——二次函数解答题1
1.定义:在平面直角坐标系中,图形上的点的纵坐标与其横坐标的差称为点的“坐标差”,而图形上所有点的“坐标差”中的最大值称为图形的“特征值”.
(1)①点的“坐标差”为 ;
②抛物线的“特征值”为 .
(2)某二次函数的“特征值”为点与点分别是此二次函数的图象与轴和轴的交点,且点与点的“坐标差”相等.
①直接写出 ;(用含的式子表示)
②求此二次函数的解析式.
(3)如图,在平面直角坐标系中,以为圆心为半径的圆与直线相交于点请直接写出⊙的“特征值”为 .
2. 如图,一次函数的图象与轴交于点与轴交于点与二次函数的图象在第一象限内交于点.
(1)求一次函数的表达式;
(2)若点在线段上,且不与点重合,与轴平行的直线与二次函数的图象相交于点求点的坐标.
3.已知二次函数的图象的顶点坐标为且图象经过点求二次函数的解析式.
4.如图,抛物线与直线相交于点且这条抛物线的对称轴为直线.
(1)若将该抛物线平移使得其经过原点,且对称轴不变,求平移后的抛物线的解析式及的值;
(2)设为直线下方的抛物线上一点,连接求面积的最大值及此时点的坐标.
5.已知:如图,二次函数的图象的顶点坐标为矩形的顶点在轴上,顶点在抛物线上,矩形在抛物线与轴所围成的图形内.
(1)求二次函数的解析式;
(2)设点的坐标为试求矩形的周长关于自变量的函数解析式,并求出自变量的取值范围.
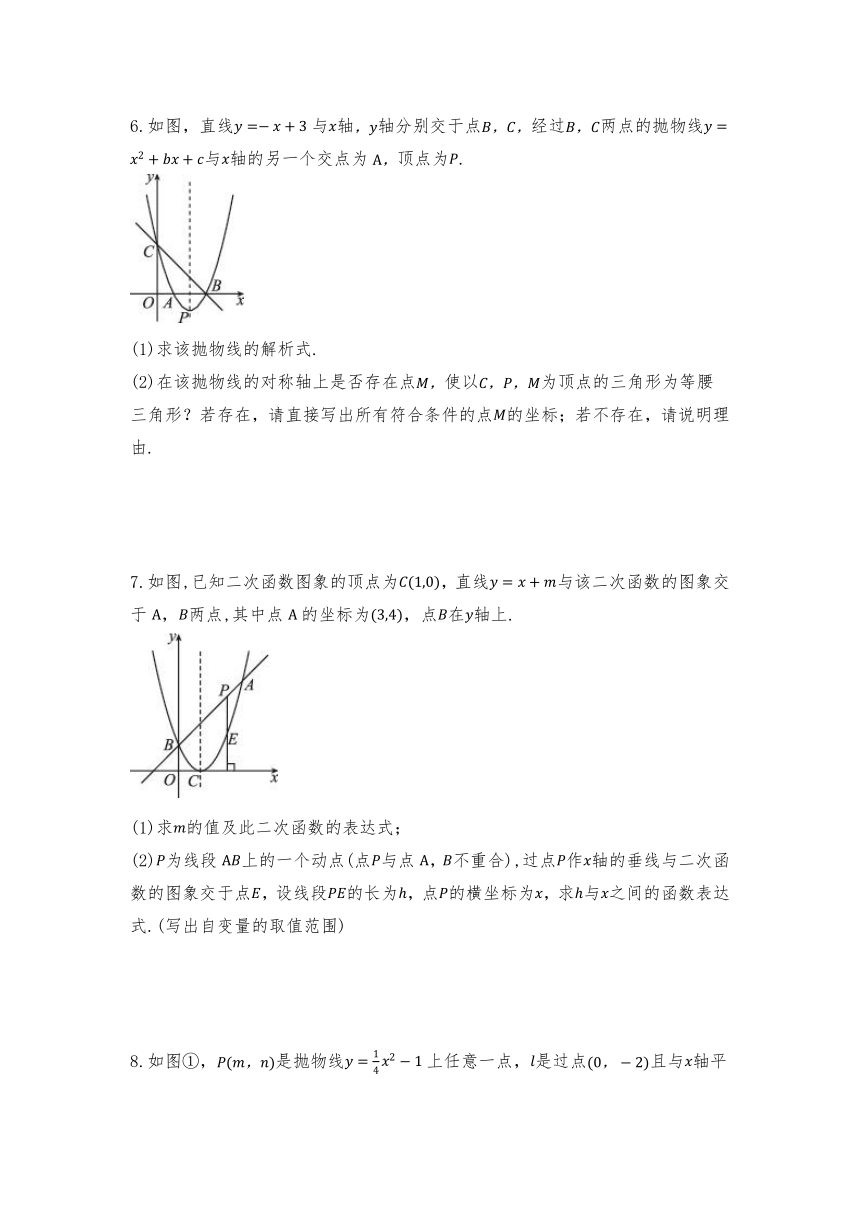
6.如图,直线与轴轴分别交于点经过两点的抛物线与轴的另一个交点为顶点为.
(1)求该抛物线的解析式.
(2)在该抛物线的对称轴上是否存在点使以为顶点的三角形为等腰三角形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.
7.如图,已知二次函数图象的顶点为,直线与该二次函数的图象交于,两点,其中点的坐标为,点在轴上.
(1)求的值及此二次函数的表达式;
(2)为线段上的一个动点(点与点,不重合),过点作轴的垂线与二次函数的图象交于点,设线段的长为,点的横坐标为,求与之间的函数表达式.(写出自变量的取值范围)
8.如图①,是抛物线上任意一点,是过点且与轴平行的直线,过点作直线,垂足为.
(1)【探究】填空:当时, , ;当时, , ;
(2)【证明】对任意的,猜想与 的大小关系,并证明你的猜想;
(3)【应用】如图②,已知点,点在抛物线上运动,当点运动到什么位置时的周长最小,求出此时点的坐标.
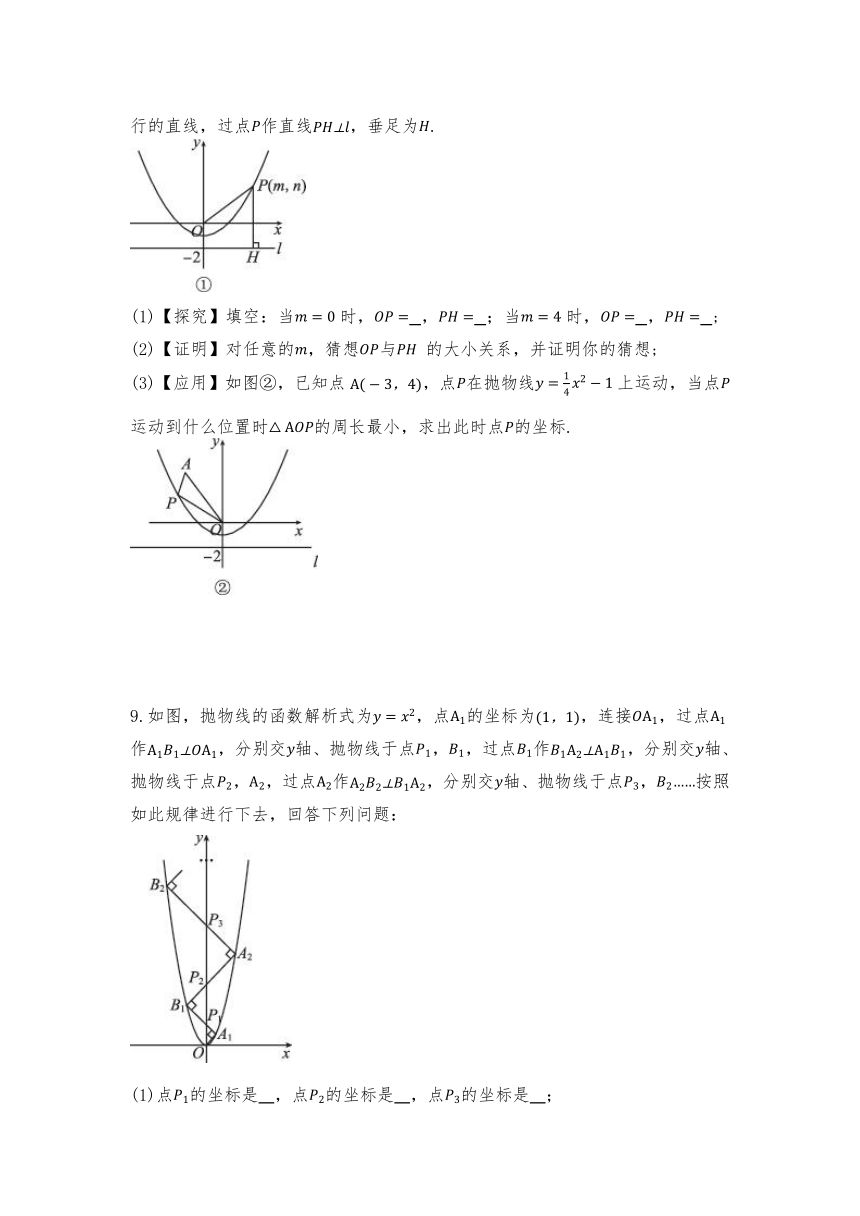
9.如图,抛物线的函数解析式为,点的坐标为,连接,过点作,分别交轴、抛物线于点,,过点作,分别交轴、抛物线于点,,过点作,分别交轴、抛物线于点,按照如此规律进行下去,回答下列问题:
(1)点的坐标是 ,点的坐标是 ,点的坐标是 ;
(2)点为正整数的坐标是 .
10.如图,二次函数的图象与轴交于点,与轴交于点,已知,.
(1)求该抛物线的解析式;
(2)沿轴平移该抛物线,使它再次经过点,求平移后的抛物线的函数解析式,并指出平移方式.
11.已知二次函数.
(1)若二次函数图象与轴有两个不同的交点,求的取值范围;
(2)二次函数的部分图象如图所示,求一元二次方程的解.
12.已知某抛物线的顶点坐标为,形状与抛物线相同,但开口方向相反.
(1)直接写出此抛物线的函数表达式;
(2)沿轴平移该抛物线,使其经过点,求出平移后的抛物线的函数表达式,并指出平移方式.
13.已知.
(1)当为何值时,是的二次函数?
(2)当为何值时,是的反比例函数?
14.如图,某小区在墙体上的点处安装一抛物线形遮阳棚,现以地面和墙体所在的直线分别为轴和轴建立直角坐标系,已知遮阳棚的高度与地面水平距离之间的关系式可以用表示,且抛物线经过点,.
请根据以上信息,解答下列问题:
(1)求抛物线的函数表达式;
(2)求遮阳棚的跨度的长;
(3)现准备在抛物线上一点处,安装一直角形钢架对遮阳棚进行加固(点分别在轴轴上,且轴轴),现有库存的钢材是否够用?
15.在平面直角坐标系中,过点且平行于轴的直线,与直线交于点点关于直线的对称点为点抛物线:经过点和点.
(1)点的坐标分别为 ;
(2)求抛物线的解析式及顶点坐标;
(3)若抛物线:与线段恰有一个公共点,请你结合函数的图象,求的取值范围.
16.如图,已知二次函数的图象经过点.
(1)求的值和该图象的顶点坐标;
(2)点在该二次函数图象上.
①当时的值为 ;
②当时,该二次函数有最小值请根据图象求出的值.
17.如图①,地面上两根等长立柱之间悬挂一根近似成抛物线的绳子.
(1)绳子最低点离地面的距离为 ;
(2)因实际需要,在离立柱 处的位置用一根立柱撑起绳子(如图②),使左边抛物线的最低点距为离地面求的长;
(3)将立柱的长度提升为通过调整的位置,使抛物线对应函数解析式的二次项系数始终为设离的距离为抛物线的顶点离地面的距离为当时,求的取值范围.
18.如图,一小球从斜坡上的点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达的最高点的坐标为解答下列问题:
(1)求抛物线的解析式;
(2)小球落点为则点的坐标为 ;
(3)在斜坡上的点处有一棵树,点的横坐标为树高为通过计算说明小球能否飞过这棵树;
(4)求小球在飞行的过程中离斜坡的最大高度.
19.如图,二次函数的图象交轴于两点,交轴于点点的坐标为顶点的坐标为.
(1)求二次函数的解析式和直线的解析式;
(2)是线段上的一个动点(端点除外),过点作轴的垂线,交抛物线于点求线段长度的最大值.
20.如图,抛物线交轴于点对称轴为直线.
(1)关于的一元二次方程的根是 ;
(2)若顶点的坐标是则方程的根是 ;
(3)试判断关于的方程的根的情况.
21.如图,抛物线与轴交于点点与轴交于点.
(1)求抛物线的解析式;
(2)在对称轴上找一点使的周长最小,求出点的坐标及周长的最小值.
22.如图,抛物线过点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点使为等腰三角形?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
23.如图,已知点,点,抛物线(,均为常数)与线段交于,两点,且,求的值.
24.已知二次函数的图象经过点.
(1)的值为 ;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在如图所给平面直角坐标系中画出该二次函数的图象;
(4)当时,求的取值范围.
1.定义:在平面直角坐标系中,图形上的点的纵坐标与其横坐标的差称为点的“坐标差”,而图形上所有点的“坐标差”中的最大值称为图形的“特征值”.
(1)①点的“坐标差”为 ;
②抛物线的“特征值”为 .
(2)某二次函数的“特征值”为点与点分别是此二次函数的图象与轴和轴的交点,且点与点的“坐标差”相等.
①直接写出 ;(用含的式子表示)
②求此二次函数的解析式.
(3)如图,在平面直角坐标系中,以为圆心为半径的圆与直线相交于点请直接写出⊙的“特征值”为 .
2. 如图,一次函数的图象与轴交于点与轴交于点与二次函数的图象在第一象限内交于点.
(1)求一次函数的表达式;
(2)若点在线段上,且不与点重合,与轴平行的直线与二次函数的图象相交于点求点的坐标.
3.已知二次函数的图象的顶点坐标为且图象经过点求二次函数的解析式.
4.如图,抛物线与直线相交于点且这条抛物线的对称轴为直线.
(1)若将该抛物线平移使得其经过原点,且对称轴不变,求平移后的抛物线的解析式及的值;
(2)设为直线下方的抛物线上一点,连接求面积的最大值及此时点的坐标.
5.已知:如图,二次函数的图象的顶点坐标为矩形的顶点在轴上,顶点在抛物线上,矩形在抛物线与轴所围成的图形内.
(1)求二次函数的解析式;
(2)设点的坐标为试求矩形的周长关于自变量的函数解析式,并求出自变量的取值范围.
6.如图,直线与轴轴分别交于点经过两点的抛物线与轴的另一个交点为顶点为.
(1)求该抛物线的解析式.
(2)在该抛物线的对称轴上是否存在点使以为顶点的三角形为等腰三角形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.
7.如图,已知二次函数图象的顶点为,直线与该二次函数的图象交于,两点,其中点的坐标为,点在轴上.
(1)求的值及此二次函数的表达式;
(2)为线段上的一个动点(点与点,不重合),过点作轴的垂线与二次函数的图象交于点,设线段的长为,点的横坐标为,求与之间的函数表达式.(写出自变量的取值范围)
8.如图①,是抛物线上任意一点,是过点且与轴平行的直线,过点作直线,垂足为.
(1)【探究】填空:当时, , ;当时, , ;
(2)【证明】对任意的,猜想与 的大小关系,并证明你的猜想;
(3)【应用】如图②,已知点,点在抛物线上运动,当点运动到什么位置时的周长最小,求出此时点的坐标.
9.如图,抛物线的函数解析式为,点的坐标为,连接,过点作,分别交轴、抛物线于点,,过点作,分别交轴、抛物线于点,,过点作,分别交轴、抛物线于点,按照如此规律进行下去,回答下列问题:
(1)点的坐标是 ,点的坐标是 ,点的坐标是 ;
(2)点为正整数的坐标是 .
10.如图,二次函数的图象与轴交于点,与轴交于点,已知,.
(1)求该抛物线的解析式;
(2)沿轴平移该抛物线,使它再次经过点,求平移后的抛物线的函数解析式,并指出平移方式.
11.已知二次函数.
(1)若二次函数图象与轴有两个不同的交点,求的取值范围;
(2)二次函数的部分图象如图所示,求一元二次方程的解.
12.已知某抛物线的顶点坐标为,形状与抛物线相同,但开口方向相反.
(1)直接写出此抛物线的函数表达式;
(2)沿轴平移该抛物线,使其经过点,求出平移后的抛物线的函数表达式,并指出平移方式.
13.已知.
(1)当为何值时,是的二次函数?
(2)当为何值时,是的反比例函数?
14.如图,某小区在墙体上的点处安装一抛物线形遮阳棚,现以地面和墙体所在的直线分别为轴和轴建立直角坐标系,已知遮阳棚的高度与地面水平距离之间的关系式可以用表示,且抛物线经过点,.
请根据以上信息,解答下列问题:
(1)求抛物线的函数表达式;
(2)求遮阳棚的跨度的长;
(3)现准备在抛物线上一点处,安装一直角形钢架对遮阳棚进行加固(点分别在轴轴上,且轴轴),现有库存的钢材是否够用?
15.在平面直角坐标系中,过点且平行于轴的直线,与直线交于点点关于直线的对称点为点抛物线:经过点和点.
(1)点的坐标分别为 ;
(2)求抛物线的解析式及顶点坐标;
(3)若抛物线:与线段恰有一个公共点,请你结合函数的图象,求的取值范围.
16.如图,已知二次函数的图象经过点.
(1)求的值和该图象的顶点坐标;
(2)点在该二次函数图象上.
①当时的值为 ;
②当时,该二次函数有最小值请根据图象求出的值.
17.如图①,地面上两根等长立柱之间悬挂一根近似成抛物线的绳子.
(1)绳子最低点离地面的距离为 ;
(2)因实际需要,在离立柱 处的位置用一根立柱撑起绳子(如图②),使左边抛物线的最低点距为离地面求的长;
(3)将立柱的长度提升为通过调整的位置,使抛物线对应函数解析式的二次项系数始终为设离的距离为抛物线的顶点离地面的距离为当时,求的取值范围.
18.如图,一小球从斜坡上的点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达的最高点的坐标为解答下列问题:
(1)求抛物线的解析式;
(2)小球落点为则点的坐标为 ;
(3)在斜坡上的点处有一棵树,点的横坐标为树高为通过计算说明小球能否飞过这棵树;
(4)求小球在飞行的过程中离斜坡的最大高度.
19.如图,二次函数的图象交轴于两点,交轴于点点的坐标为顶点的坐标为.
(1)求二次函数的解析式和直线的解析式;
(2)是线段上的一个动点(端点除外),过点作轴的垂线,交抛物线于点求线段长度的最大值.
20.如图,抛物线交轴于点对称轴为直线.
(1)关于的一元二次方程的根是 ;
(2)若顶点的坐标是则方程的根是 ;
(3)试判断关于的方程的根的情况.
21.如图,抛物线与轴交于点点与轴交于点.
(1)求抛物线的解析式;
(2)在对称轴上找一点使的周长最小,求出点的坐标及周长的最小值.
22.如图,抛物线过点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点使为等腰三角形?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
23.如图,已知点,点,抛物线(,均为常数)与线段交于,两点,且,求的值.
24.已知二次函数的图象经过点.
(1)的值为 ;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在如图所给平面直角坐标系中画出该二次函数的图象;
(4)当时,求的取值范围.
同课章节目录
