2023中考数学三轮冲刺复习——二次函数应用02(无答案)
文档属性
| 名称 | 2023中考数学三轮冲刺复习——二次函数应用02(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:44:55 | ||
图片预览


文档简介
2023中考数学三轮冲刺复习——二次函数应用02
1.喜迎圣诞,某商店销售一种进价为元件的商品,售价为元件,每星期可卖出件,若每件商品的售价每上涨元,则每星期就会少卖出件设每件商品的售价上涨元为正整数,每星期销售该商品的利润为元,则与之间的函数表达式为( )
A. B.
C. D.
2.某书城某畅销书的售价为每本元,每星期可卖出本,书城准备开展“读书节活动”降价促销.经调研,如果此畅销书每本的售价每降低元,每星期可多卖出本.设每本畅销书降价元,每星期售出此畅销书的总销售额为元,则与之间的函数表达式为( )
A. B.
C. D.
3.用的绳子围成一个矩形,则矩形面积与一边长之间的函数关系式为( )
A. B.
C. D.
4.用长的铝合金条制成如图所示形状的矩形窗框,这个窗户的最大透光面积为( )
A. B. C. D.
5.如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为顶点距水面小孔顶点距水面.当水位上涨刚好淹没小孔时,大孔的水面宽度为( )
A. B. C. D.
6.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则当的长为 时,围成的矩形区域的面积最大.
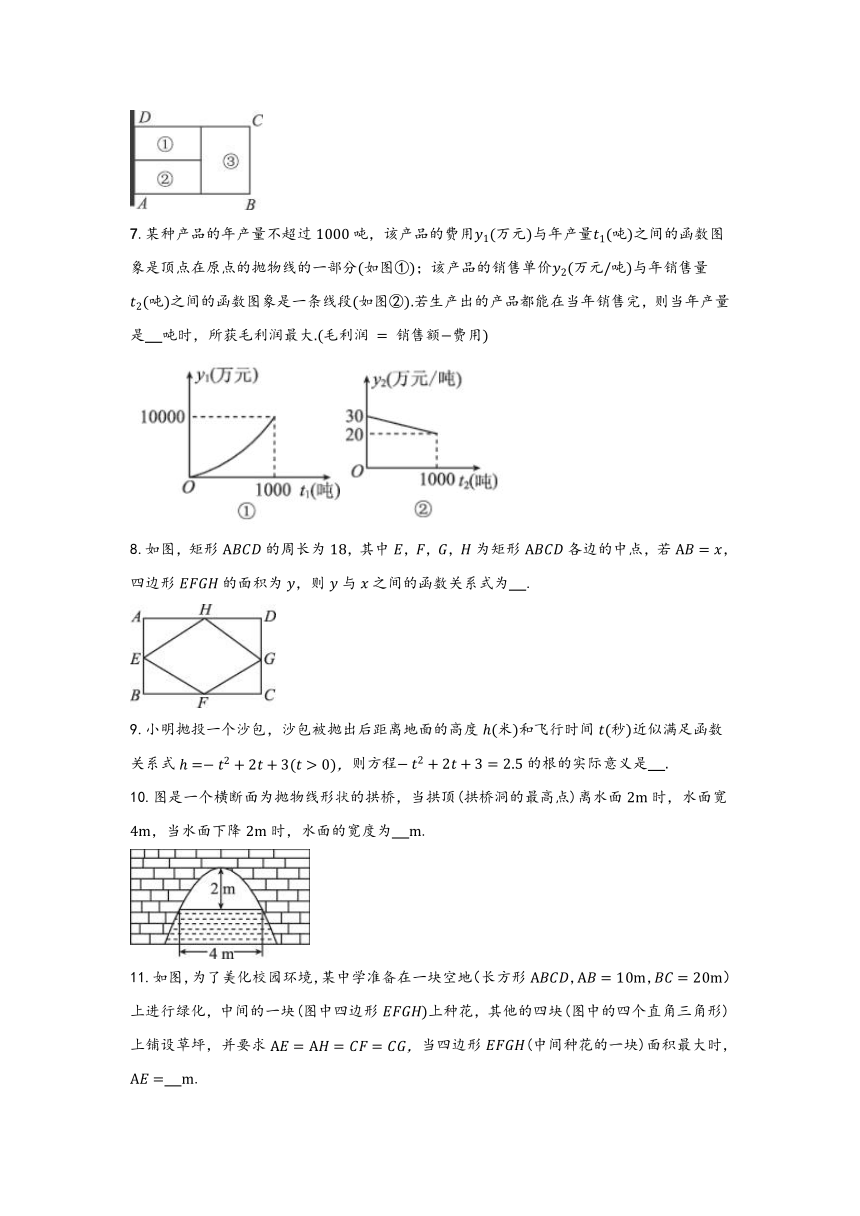
7.某种产品的年产量不超过吨,该产品的费用万元与年产量吨之间的函数图象是顶点在原点的抛物线的一部分如图①;该产品的销售单价万元吨与年销售量吨之间的函数图象是一条线段如图②若生产出的产品都能在当年销售完,则当年产量是 吨时,所获毛利润最大毛利润 销售额费用
8.如图,矩形的周长为,其中,,,为矩形各边的中点,若,四边形的面积为,则与之间的函数关系式为 .
9.小明抛投一个沙包,沙包被抛出后距离地面的高度米和飞行时间秒近似满足函数关系式则方程的根的实际意义是
10.图是一个横断面为抛物线形状的拱桥,当拱顶(拱桥洞的最高点)离水面时,水面宽,当水面下降时,水面的宽度为 .
11.如图,为了美化校园环境,某中学准备在一块空地(长方形,,)上进行绿化,中间的一块(图中四边形上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求当四边形(中间种花的一块)面积最大时, .
12.某景区的一个景点的门票为每人元时,参观该景点的人数每天达到人,门票价格每人每上涨元,每天参观该景点的人数就会减少人,门票定价不得低于元/人,不得高于元/人.求该景点每天门票收入(元)关于门票定价(元/人)的函数表达式.
13.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围两边),设花园的面积为.
(1)若花园的面积为,求的值;
(2)写出花园的面积与之间的函数表达式.当为何值时,花园的面积最大?最大为多少?
(3)若在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园的面积的最大值.
14.某商场以每件元的价格购进一种商品,在试销中发现这种商品的日销售量(件)与每件的销售价(元)满足,其中销售价不能低于进价,且日销售量不能为.
(1)每件商品的利润是 元;(用含的代数式表示)
(2)写出商场卖这种商品的日销售利润(元)与每件的销售价(元)之间的函数表达式(结果化为一般形式),并指出自变量的取值范围.
15.如图,某小区在墙体上的点处安装一抛物线形遮阳棚,现以地面和墙体所在的直线分别为轴和轴建立直角坐标系,已知遮阳棚的高度与地面水平距离之间的关系式可以用表示,且抛物线经过点,.
请根据以上信息,解答下列问题:
(1)求抛物线的函数表达式;
(2)求遮阳棚的跨度的长;
(3)现准备在抛物线上一点处,安装一直角形钢架对遮阳棚进行加固(点分别在轴轴上,且轴轴),现有库存的钢材是否够用?
16.如图,某学生的一次抛物线形传球,球出手(点处)时离地面的高度是,出手后球沿抛物线运动到最高点时,运行高度,水平距离.
(1)试求篮球运行的高度与水平距离之间的函数表达式;(不用体现自变量的取值范围)
(2)若队友接球的最佳高度为,则队友在距这名学生多远处接球最佳?
17.行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某型号汽车的刹车性能(车速不超过对这种汽车进行测试,测得数据如下表:
刹车时的车速 …
刹车距离 …
(1)建立适当的平面直角坐标系,根据上表中与的对应值,描出相应的点,并作出关于的函数的大致图象.
(2)这种型号汽车车速为时,刹车距离为多少?
(3)该型号汽车发生了一次交通事故,现场测得刹车距离为,推测刹车时的车速是多少?事故发生时,汽车是超速行驶还是正常行驶?
18.如图,从某建筑物米高的窗口处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点离墙米,离地面米,建立如图所示的平面直角坐标系.
(1)求抛物线的函数表达式;
(2)求水流落地点离墙的距离.
19.如图,在一块长米、宽米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为∶,设竖甬道的宽度为米,草坪的面积为平方米.
(1)与之间的函数表达式为 ;(不用体现自变量的取值范围)
(2)若草坪的面积为平方米,请求出竖甬道的宽度.
20.学校“科技创新”社团向市场推出一种新型电子产品,试销发现:该电子产品的销售价格(元/件)与销售量(件)之间满足一次函数关系,其图象如图所示,已知该产品的成本价是元/件.
(1)求与之间的函数表达式;
(2)求销售利润(元)关于销售量(件)的函数表达式,当销售量为多少时,销售利润最大?最大值是多少?
1.喜迎圣诞,某商店销售一种进价为元件的商品,售价为元件,每星期可卖出件,若每件商品的售价每上涨元,则每星期就会少卖出件设每件商品的售价上涨元为正整数,每星期销售该商品的利润为元,则与之间的函数表达式为( )
A. B.
C. D.
2.某书城某畅销书的售价为每本元,每星期可卖出本,书城准备开展“读书节活动”降价促销.经调研,如果此畅销书每本的售价每降低元,每星期可多卖出本.设每本畅销书降价元,每星期售出此畅销书的总销售额为元,则与之间的函数表达式为( )
A. B.
C. D.
3.用的绳子围成一个矩形,则矩形面积与一边长之间的函数关系式为( )
A. B.
C. D.
4.用长的铝合金条制成如图所示形状的矩形窗框,这个窗户的最大透光面积为( )
A. B. C. D.
5.如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为顶点距水面小孔顶点距水面.当水位上涨刚好淹没小孔时,大孔的水面宽度为( )
A. B. C. D.
6.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则当的长为 时,围成的矩形区域的面积最大.
7.某种产品的年产量不超过吨,该产品的费用万元与年产量吨之间的函数图象是顶点在原点的抛物线的一部分如图①;该产品的销售单价万元吨与年销售量吨之间的函数图象是一条线段如图②若生产出的产品都能在当年销售完,则当年产量是 吨时,所获毛利润最大毛利润 销售额费用
8.如图,矩形的周长为,其中,,,为矩形各边的中点,若,四边形的面积为,则与之间的函数关系式为 .
9.小明抛投一个沙包,沙包被抛出后距离地面的高度米和飞行时间秒近似满足函数关系式则方程的根的实际意义是
10.图是一个横断面为抛物线形状的拱桥,当拱顶(拱桥洞的最高点)离水面时,水面宽,当水面下降时,水面的宽度为 .
11.如图,为了美化校园环境,某中学准备在一块空地(长方形,,)上进行绿化,中间的一块(图中四边形上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求当四边形(中间种花的一块)面积最大时, .
12.某景区的一个景点的门票为每人元时,参观该景点的人数每天达到人,门票价格每人每上涨元,每天参观该景点的人数就会减少人,门票定价不得低于元/人,不得高于元/人.求该景点每天门票收入(元)关于门票定价(元/人)的函数表达式.
13.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围两边),设花园的面积为.
(1)若花园的面积为,求的值;
(2)写出花园的面积与之间的函数表达式.当为何值时,花园的面积最大?最大为多少?
(3)若在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园的面积的最大值.
14.某商场以每件元的价格购进一种商品,在试销中发现这种商品的日销售量(件)与每件的销售价(元)满足,其中销售价不能低于进价,且日销售量不能为.
(1)每件商品的利润是 元;(用含的代数式表示)
(2)写出商场卖这种商品的日销售利润(元)与每件的销售价(元)之间的函数表达式(结果化为一般形式),并指出自变量的取值范围.
15.如图,某小区在墙体上的点处安装一抛物线形遮阳棚,现以地面和墙体所在的直线分别为轴和轴建立直角坐标系,已知遮阳棚的高度与地面水平距离之间的关系式可以用表示,且抛物线经过点,.
请根据以上信息,解答下列问题:
(1)求抛物线的函数表达式;
(2)求遮阳棚的跨度的长;
(3)现准备在抛物线上一点处,安装一直角形钢架对遮阳棚进行加固(点分别在轴轴上,且轴轴),现有库存的钢材是否够用?
16.如图,某学生的一次抛物线形传球,球出手(点处)时离地面的高度是,出手后球沿抛物线运动到最高点时,运行高度,水平距离.
(1)试求篮球运行的高度与水平距离之间的函数表达式;(不用体现自变量的取值范围)
(2)若队友接球的最佳高度为,则队友在距这名学生多远处接球最佳?
17.行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某型号汽车的刹车性能(车速不超过对这种汽车进行测试,测得数据如下表:
刹车时的车速 …
刹车距离 …
(1)建立适当的平面直角坐标系,根据上表中与的对应值,描出相应的点,并作出关于的函数的大致图象.
(2)这种型号汽车车速为时,刹车距离为多少?
(3)该型号汽车发生了一次交通事故,现场测得刹车距离为,推测刹车时的车速是多少?事故发生时,汽车是超速行驶还是正常行驶?
18.如图,从某建筑物米高的窗口处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点离墙米,离地面米,建立如图所示的平面直角坐标系.
(1)求抛物线的函数表达式;
(2)求水流落地点离墙的距离.
19.如图,在一块长米、宽米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为∶,设竖甬道的宽度为米,草坪的面积为平方米.
(1)与之间的函数表达式为 ;(不用体现自变量的取值范围)
(2)若草坪的面积为平方米,请求出竖甬道的宽度.
20.学校“科技创新”社团向市场推出一种新型电子产品,试销发现:该电子产品的销售价格(元/件)与销售量(件)之间满足一次函数关系,其图象如图所示,已知该产品的成本价是元/件.
(1)求与之间的函数表达式;
(2)求销售利润(元)关于销售量(件)的函数表达式,当销售量为多少时,销售利润最大?最大值是多少?
同课章节目录
