2023年中考数学三轮冲刺复习——二次函数应用03(无答案)
文档属性
| 名称 | 2023年中考数学三轮冲刺复习——二次函数应用03(无答案) | 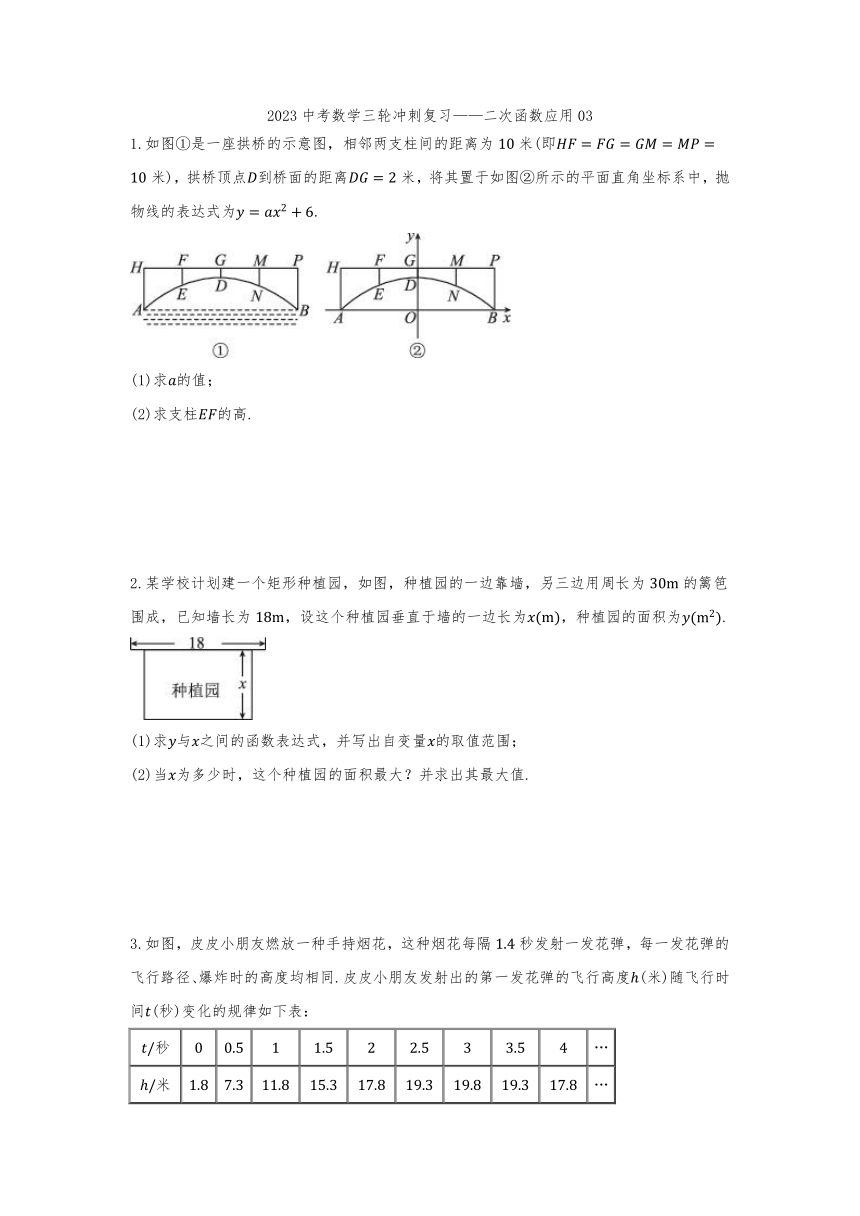 | |
| 格式 | docx | ||
| 文件大小 | 154.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:51:39 | ||
图片预览





文档简介
2023中考数学三轮冲刺复习——二次函数应用03
1.如图①是一座拱桥的示意图,相邻两支柱间的距离为米(即米),拱桥顶点到桥面的距离米,将其置于如图②所示的平面直角坐标系中,抛物线的表达式为.
(1)求的值;
(2)求支柱的高.
2.某学校计划建一个矩形种植园,如图,种植园的一边靠墙,另三边用周长为的篱笆围成,已知墙长为,设这个种植园垂直于墙的一边长为,种植园的面积为.
(1)求与之间的函数表达式,并写出自变量的取值范围;
(2)当为多少时,这个种植园的面积最大?并求出其最大值.
3.如图,皮皮小朋友燃放一种手持烟花,这种烟花每隔秒发射一发花弹,每一发花弹的飞行路径、爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度(米)随飞行时间(秒)变化的规律如下表:
秒 …
米 …
(1)根据这些数据在图②的坐标系中描出相应的点,选择适当的函数表示与之间的关系,并求出相应的函数表达式;
(2)为了安全,要求花弹爆炸时的高度不低于米.皮皮发现在第一发花弹爆炸的同时,第三发花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.
4.某商店原来平均每天可销售某种水果千克,每千克可盈利元,为减少库存,现决定降价销售.经市场调查发现,如果这种水果每千克每降价元,那么每天可多售出千克.
(1)设每千克水果降价元,平均每天盈利元,则关于的函数表达式为 ;(不要求写自变量的取值范围)
(2)若要平均每天盈利元,则每千克应降价多少元?
5.某旅游地在年“五一”小长假期间,接待游客达万人次.在该旅游地,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗元,借鉴以往经验,若每碗卖元,平均每天将销售碗,若价格每提高元,则平均每天少销售碗,每天店面所需其他各种费用为元.
(1)若该旅游地在年“五一”小长假期间,接待游客万人次,求出年至年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护旅游地形象,物价局规定每碗售价不得超过元,则当每碗售价定为多少元时,店家才能实现每天净利润最大?最大净利润是多少?(净利润=总收入-总成本-其他各种费用)
6.如图①,地面上两根等长立柱之间悬挂一根近似成抛物线的绳子.
(1)绳子最低点离地面的距离为 ;
(2)因实际需要,在离立柱 处的位置用一根立柱撑起绳子(如图②),使左边抛物线的最低点距为离地面求的长;
(3)将立柱的长度提升为通过调整的位置,使抛物线对应函数解析式的二次项系数始终为设离的距离为抛物线的顶点离地面的距离为当时,求的取值范围.
7.用各种盛水容器可以制作精致的家用流水景观(如图①).
科学原理:如图②,始终盛满水的圆柱体水桶水面离地面的高度为(单位:如果在离水面竖直距离为(单位:的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离(单位:与的关系为.
应用思考:现用高度为的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离处开一个小孔.
(1)与之间的关系式为 (不必写出自变量的取值范围),当为 时,射程有最大
值,最大射程是 ;
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为要使两孔射出水的射程相同,求之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加求垫高的高度及小孔离水面的竖直距离.
8.如图,一小球从斜坡上的点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达的最高点的坐标为解答下列问题:
(1)求抛物线的解析式;
(2)小球落点为则点的坐标为 ;
(3)在斜坡上的点处有一棵树,点的横坐标为树高为通过计算说明小球能否飞过这棵树;
(4)求小球在飞行的过程中离斜坡的最大高度.
9.为推进“书香社区”建设,某社区计划购进一批图书.已知购买本科技类图书和本文学类图书需元,购买本科技类图书和本文学类图书需元.
(1)科技类图书与文学类图书的单价分别为 ;
(2)为了支持“书香社区”建设,助推科技发展,商家对科技类图书推出销售优惠活动(文学类图书售价不变):购买科技类图书超过本但不超过本时,每增加本,单价降低
元;超过本时,均按购买本时的单价销售.社区计划购进两种图书共计本,其中科技类图书不少于本,但不超过本.按此优惠,社区至少需要准备多少元购书款?
10.某超市经销一种商品,每件成本为元.经市场调研,当该商品每件的销售价为元时,每个月可销售件,若每件的销售价每增加元,则每个月的销售量将减少件.设该商品每件的销售价为元,每个月的销售量为件.
(1)与之间的函数解析式为 ;(不必写出自变量的取值范围)
(2)当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少元?
11.如图,在中,,,,动点从点开始沿边向点以的速度移动(不与点重合),动点从点开始沿边向点以的速度移动(不与点重合).如果点分别从点同时出发,设移动的时间为四边形的面积为.
(1)求与之间的函数关系式;
(2)自变量的取值范围为 ;
(3)四边形的面积能否等于?若能,求出移动的时间;若不能,请说明理由.
12.如图,二次函数的图象交轴于两点,交轴于点点的坐标为顶点的坐标为.
(1)求二次函数的解析式和直线的解析式;
(2)是线段上的一个动点(端点除外),过点作轴的垂线,交抛物线于点求线段长度的最大值.
13.某文具店购进一批单价为元的学习用品,按照相关部门规定其销售单价不低于进价,且不高于进价的倍,通过分析销售情况,发现每天的销售量(件)与销售单价(元)满足一次函数关系,且当时;当时.
(1)求与之间的函数解析式;
(2)这种学习用品的销售单价定为多少时,每天可获得最大利润?最大利润是多少元?
14.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个元.经市场调查发现,这种双肩包每天的销售量(个)与销售单价(元/个)有如下关系:且为整数).设这种双肩包每天的销售利润为元.
(1)与之间的函数关系式为 ;
(2)这种双肩包的销售单价定为多少元/个时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不能高于元/个,该商店销售这种双肩包每天要获得元的销售利润,销售单价应定为多少元/个?
15.如图是某公园一喷水池(示意图),在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度与水平距离之间的函数关系式为.
(1)喷出的水流离地面的最大高度为 ;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
16.随着时代的不断发展,网络购物已经融入人们的生活中,某电商平台上一个商家出售一种成本为元件的恤衫根据后台数据发现,以单价元件销售,每天可以销售件,若每件每降价元,则销量就增加件设销售单价为元件,每天的销量为件
(1)求与之间的函数关系式(不用体现自变量的取值范围);
(2)根据该电商平台的规定每销售一件恤衫商家需缴纳电商平台推广费用元,当销售单价是多少时,该商家每天获得的利润(元)最大,最大利润是多少?
17.某旅行社组团去外地旅游人起组团,每人单价元.旅行社对超过人的团给予优惠,即旅游团每增加一人,每人的单价就降低元.你能帮助算一下,当一个旅游团的人数是多少时,旅行社可以获得最大营业额?最大营业额是多少?
18.某商店销售一种销售成本为每件元的玩具,若按每件元销售,一个月可售出件,销售价每涨元,月销量就减少件设销售价为每件元月销量为件,月销售利润为元
(1)写出与之间的函数关系式和与之间的函数关系式;
(2)商店要在月销售成本不超过的情况下,使月销售利润达到元,销售价应定为每件多少元?
(3)当销售价定为每件多少元时会获得最大利润?并求出最大利润
19.某网店销售一种儿童玩具,进价为每件元,物价部门规定每件儿童玩具的销售利润不高于进价的在销售过程中发现,这种儿童玩具每天的销售量件与销售单价元件满足一次函数关系当销售单价为元件时,每天的销售量为件当销售单价为元件时,每天的销售量为件求销售单价是多少时,该网店销售这种儿童玩具每天获得的利润最大,并求此时的最大利润
20.抗击“新冠”疫情后期,我国的医疗物资供给和销售已经正常,某药店销售每瓶进价为元的消毒洗手液,市场调查发现,若以每瓶元的价格销售,平均每天销售瓶,单价每提高元,平均每天就少销售瓶.
(1)平均每天的销售量瓶与销售价元瓶之间的函数关系式为
(2)求该药店平均每天的销售利润(元)与销售价(元/瓶)之间的函数关系式;
(3)当每瓶的销售价为多少元时,可以获得最大利润?最大利润是多少元?
21.有长为的篱笆,一边利用墙墙的最大可用长度为围成如图所示的矩形花圃设花圃边,面积为
(1)写出与之间的关系式,并指出的取值范围;
(2)当分别为多少米时,花圃面积最大?最大面积为多少?
22.如图,一位篮球运动员在离篮圈水平距离处跳起投篮,球运行的高度与运行的水平距离满足关系式.球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面的距离为.
(1)当球运行的水平距离为多少时达到最大高度?最大高度为多少?
(2)若该运动员身高,这次跳投时,球在他头顶上方处出手,则球出手时,他跳离地面多高?
23.如图①是边长为的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得四个点重合于图②中的点处,正好得到一个长方体形状的包装盒.图①中,点在边上,且是被切去的一个等腰直角三角形斜边的两个端点,设.
(1)若要求包装盒的高是(以图中所示位置为参照),则的值应是多少?
(2)某广告商要求包装盒的侧面积最大,则应取何值?
24.如图(示意图),已知排球场的长度为米,位于球场中线处球网的高度为米,一队员站在点处发球,排球从点的正上方米的点向正前方飞出,当排球运行至离点的水平距离为米时,到达最高点建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为米时,求排球飞行的高度(单位:米)与水平距离(单位:米)之间的函数关系式(不要求写自变量的取值范围);
(2)在的条件下,对方距球网米的点处有一队员,她起跳后的最大高度为米,则这次她是否可以拦网成功?请通过计算说明;
(3)若队员发球既要过球网,又不出边界,则排球飞行的最大高度(单位:米)的取值范围是多少(排球压线不算出界)?
25.小哲的姑妈经营一家花店,随着越来越多的人喜爱多肉植物,姑妈也打算销售多肉植物.小哲帮助姑妈针对某种多肉植物做了市场调查后,绘制了以下两幅图,如图(单株成本
月份最低,图①中的图象是直线,图②中的图象是抛物线).
(1)如果在月份出售这种植物,那么单株获利 元;
(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大.(提示:单株获利=单株售价-单株成本)
26.如图所示,施工队要修建一个横断面为抛物线的公路隧道的宽度为米,其顶点到的距离为米.
(1)请建立适当的平面直角坐标系,并求出这条抛物线所对应的函数表达式;
(2)隧道下的公路是双向行车道(正中间是一条宽米的隔离带),其中的一条行车道能否行驶宽米、高米的特种车辆?请通过计算说明.
27.如图,在中,动点从点开始沿边向点以的速度运动(不与点重合),动点从点开始沿边向点以的速度运动(不与点重合).如果点分别从点同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动的时间为四边形的面积为.
(1)求与之间的函数关系式,并写出自变量的取值范围.
(2)四边形的面积能否等于?若能,请求出运动的时间;若不能,请说明理由.
28.红星公司销售一种成本为元/件的产品,若月销售单价不高于元/件,一个月可售出万件;月销售单价每涨价元/件,月销售量就减少万件.其中月销售单价不低于成本.设月销售单价为(单位:元/件),月销售量为(单位:万件).
(1)直接写出与之间的函数关系式,并写出自变量的取值范围;
(2)当月销售单价是多少元/件时,月销售利润最大,最大月销售利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售件产品便向大别山区捐款元.已知该公司捐款当月的月销售单价不高于元/件,最大月销售利润是万元,求的值.
1.如图①是一座拱桥的示意图,相邻两支柱间的距离为米(即米),拱桥顶点到桥面的距离米,将其置于如图②所示的平面直角坐标系中,抛物线的表达式为.
(1)求的值;
(2)求支柱的高.
2.某学校计划建一个矩形种植园,如图,种植园的一边靠墙,另三边用周长为的篱笆围成,已知墙长为,设这个种植园垂直于墙的一边长为,种植园的面积为.
(1)求与之间的函数表达式,并写出自变量的取值范围;
(2)当为多少时,这个种植园的面积最大?并求出其最大值.
3.如图,皮皮小朋友燃放一种手持烟花,这种烟花每隔秒发射一发花弹,每一发花弹的飞行路径、爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度(米)随飞行时间(秒)变化的规律如下表:
秒 …
米 …
(1)根据这些数据在图②的坐标系中描出相应的点,选择适当的函数表示与之间的关系,并求出相应的函数表达式;
(2)为了安全,要求花弹爆炸时的高度不低于米.皮皮发现在第一发花弹爆炸的同时,第三发花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.
4.某商店原来平均每天可销售某种水果千克,每千克可盈利元,为减少库存,现决定降价销售.经市场调查发现,如果这种水果每千克每降价元,那么每天可多售出千克.
(1)设每千克水果降价元,平均每天盈利元,则关于的函数表达式为 ;(不要求写自变量的取值范围)
(2)若要平均每天盈利元,则每千克应降价多少元?
5.某旅游地在年“五一”小长假期间,接待游客达万人次.在该旅游地,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗元,借鉴以往经验,若每碗卖元,平均每天将销售碗,若价格每提高元,则平均每天少销售碗,每天店面所需其他各种费用为元.
(1)若该旅游地在年“五一”小长假期间,接待游客万人次,求出年至年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护旅游地形象,物价局规定每碗售价不得超过元,则当每碗售价定为多少元时,店家才能实现每天净利润最大?最大净利润是多少?(净利润=总收入-总成本-其他各种费用)
6.如图①,地面上两根等长立柱之间悬挂一根近似成抛物线的绳子.
(1)绳子最低点离地面的距离为 ;
(2)因实际需要,在离立柱 处的位置用一根立柱撑起绳子(如图②),使左边抛物线的最低点距为离地面求的长;
(3)将立柱的长度提升为通过调整的位置,使抛物线对应函数解析式的二次项系数始终为设离的距离为抛物线的顶点离地面的距离为当时,求的取值范围.
7.用各种盛水容器可以制作精致的家用流水景观(如图①).
科学原理:如图②,始终盛满水的圆柱体水桶水面离地面的高度为(单位:如果在离水面竖直距离为(单位:的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离(单位:与的关系为.
应用思考:现用高度为的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离处开一个小孔.
(1)与之间的关系式为 (不必写出自变量的取值范围),当为 时,射程有最大
值,最大射程是 ;
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为要使两孔射出水的射程相同,求之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加求垫高的高度及小孔离水面的竖直距离.
8.如图,一小球从斜坡上的点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达的最高点的坐标为解答下列问题:
(1)求抛物线的解析式;
(2)小球落点为则点的坐标为 ;
(3)在斜坡上的点处有一棵树,点的横坐标为树高为通过计算说明小球能否飞过这棵树;
(4)求小球在飞行的过程中离斜坡的最大高度.
9.为推进“书香社区”建设,某社区计划购进一批图书.已知购买本科技类图书和本文学类图书需元,购买本科技类图书和本文学类图书需元.
(1)科技类图书与文学类图书的单价分别为 ;
(2)为了支持“书香社区”建设,助推科技发展,商家对科技类图书推出销售优惠活动(文学类图书售价不变):购买科技类图书超过本但不超过本时,每增加本,单价降低
元;超过本时,均按购买本时的单价销售.社区计划购进两种图书共计本,其中科技类图书不少于本,但不超过本.按此优惠,社区至少需要准备多少元购书款?
10.某超市经销一种商品,每件成本为元.经市场调研,当该商品每件的销售价为元时,每个月可销售件,若每件的销售价每增加元,则每个月的销售量将减少件.设该商品每件的销售价为元,每个月的销售量为件.
(1)与之间的函数解析式为 ;(不必写出自变量的取值范围)
(2)当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少元?
11.如图,在中,,,,动点从点开始沿边向点以的速度移动(不与点重合),动点从点开始沿边向点以的速度移动(不与点重合).如果点分别从点同时出发,设移动的时间为四边形的面积为.
(1)求与之间的函数关系式;
(2)自变量的取值范围为 ;
(3)四边形的面积能否等于?若能,求出移动的时间;若不能,请说明理由.
12.如图,二次函数的图象交轴于两点,交轴于点点的坐标为顶点的坐标为.
(1)求二次函数的解析式和直线的解析式;
(2)是线段上的一个动点(端点除外),过点作轴的垂线,交抛物线于点求线段长度的最大值.
13.某文具店购进一批单价为元的学习用品,按照相关部门规定其销售单价不低于进价,且不高于进价的倍,通过分析销售情况,发现每天的销售量(件)与销售单价(元)满足一次函数关系,且当时;当时.
(1)求与之间的函数解析式;
(2)这种学习用品的销售单价定为多少时,每天可获得最大利润?最大利润是多少元?
14.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个元.经市场调查发现,这种双肩包每天的销售量(个)与销售单价(元/个)有如下关系:且为整数).设这种双肩包每天的销售利润为元.
(1)与之间的函数关系式为 ;
(2)这种双肩包的销售单价定为多少元/个时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不能高于元/个,该商店销售这种双肩包每天要获得元的销售利润,销售单价应定为多少元/个?
15.如图是某公园一喷水池(示意图),在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度与水平距离之间的函数关系式为.
(1)喷出的水流离地面的最大高度为 ;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
16.随着时代的不断发展,网络购物已经融入人们的生活中,某电商平台上一个商家出售一种成本为元件的恤衫根据后台数据发现,以单价元件销售,每天可以销售件,若每件每降价元,则销量就增加件设销售单价为元件,每天的销量为件
(1)求与之间的函数关系式(不用体现自变量的取值范围);
(2)根据该电商平台的规定每销售一件恤衫商家需缴纳电商平台推广费用元,当销售单价是多少时,该商家每天获得的利润(元)最大,最大利润是多少?
17.某旅行社组团去外地旅游人起组团,每人单价元.旅行社对超过人的团给予优惠,即旅游团每增加一人,每人的单价就降低元.你能帮助算一下,当一个旅游团的人数是多少时,旅行社可以获得最大营业额?最大营业额是多少?
18.某商店销售一种销售成本为每件元的玩具,若按每件元销售,一个月可售出件,销售价每涨元,月销量就减少件设销售价为每件元月销量为件,月销售利润为元
(1)写出与之间的函数关系式和与之间的函数关系式;
(2)商店要在月销售成本不超过的情况下,使月销售利润达到元,销售价应定为每件多少元?
(3)当销售价定为每件多少元时会获得最大利润?并求出最大利润
19.某网店销售一种儿童玩具,进价为每件元,物价部门规定每件儿童玩具的销售利润不高于进价的在销售过程中发现,这种儿童玩具每天的销售量件与销售单价元件满足一次函数关系当销售单价为元件时,每天的销售量为件当销售单价为元件时,每天的销售量为件求销售单价是多少时,该网店销售这种儿童玩具每天获得的利润最大,并求此时的最大利润
20.抗击“新冠”疫情后期,我国的医疗物资供给和销售已经正常,某药店销售每瓶进价为元的消毒洗手液,市场调查发现,若以每瓶元的价格销售,平均每天销售瓶,单价每提高元,平均每天就少销售瓶.
(1)平均每天的销售量瓶与销售价元瓶之间的函数关系式为
(2)求该药店平均每天的销售利润(元)与销售价(元/瓶)之间的函数关系式;
(3)当每瓶的销售价为多少元时,可以获得最大利润?最大利润是多少元?
21.有长为的篱笆,一边利用墙墙的最大可用长度为围成如图所示的矩形花圃设花圃边,面积为
(1)写出与之间的关系式,并指出的取值范围;
(2)当分别为多少米时,花圃面积最大?最大面积为多少?
22.如图,一位篮球运动员在离篮圈水平距离处跳起投篮,球运行的高度与运行的水平距离满足关系式.球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面的距离为.
(1)当球运行的水平距离为多少时达到最大高度?最大高度为多少?
(2)若该运动员身高,这次跳投时,球在他头顶上方处出手,则球出手时,他跳离地面多高?
23.如图①是边长为的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得四个点重合于图②中的点处,正好得到一个长方体形状的包装盒.图①中,点在边上,且是被切去的一个等腰直角三角形斜边的两个端点,设.
(1)若要求包装盒的高是(以图中所示位置为参照),则的值应是多少?
(2)某广告商要求包装盒的侧面积最大,则应取何值?
24.如图(示意图),已知排球场的长度为米,位于球场中线处球网的高度为米,一队员站在点处发球,排球从点的正上方米的点向正前方飞出,当排球运行至离点的水平距离为米时,到达最高点建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为米时,求排球飞行的高度(单位:米)与水平距离(单位:米)之间的函数关系式(不要求写自变量的取值范围);
(2)在的条件下,对方距球网米的点处有一队员,她起跳后的最大高度为米,则这次她是否可以拦网成功?请通过计算说明;
(3)若队员发球既要过球网,又不出边界,则排球飞行的最大高度(单位:米)的取值范围是多少(排球压线不算出界)?
25.小哲的姑妈经营一家花店,随着越来越多的人喜爱多肉植物,姑妈也打算销售多肉植物.小哲帮助姑妈针对某种多肉植物做了市场调查后,绘制了以下两幅图,如图(单株成本
月份最低,图①中的图象是直线,图②中的图象是抛物线).
(1)如果在月份出售这种植物,那么单株获利 元;
(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大.(提示:单株获利=单株售价-单株成本)
26.如图所示,施工队要修建一个横断面为抛物线的公路隧道的宽度为米,其顶点到的距离为米.
(1)请建立适当的平面直角坐标系,并求出这条抛物线所对应的函数表达式;
(2)隧道下的公路是双向行车道(正中间是一条宽米的隔离带),其中的一条行车道能否行驶宽米、高米的特种车辆?请通过计算说明.
27.如图,在中,动点从点开始沿边向点以的速度运动(不与点重合),动点从点开始沿边向点以的速度运动(不与点重合).如果点分别从点同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动的时间为四边形的面积为.
(1)求与之间的函数关系式,并写出自变量的取值范围.
(2)四边形的面积能否等于?若能,请求出运动的时间;若不能,请说明理由.
28.红星公司销售一种成本为元/件的产品,若月销售单价不高于元/件,一个月可售出万件;月销售单价每涨价元/件,月销售量就减少万件.其中月销售单价不低于成本.设月销售单价为(单位:元/件),月销售量为(单位:万件).
(1)直接写出与之间的函数关系式,并写出自变量的取值范围;
(2)当月销售单价是多少元/件时,月销售利润最大,最大月销售利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售件产品便向大别山区捐款元.已知该公司捐款当月的月销售单价不高于元/件,最大月销售利润是万元,求的值.
同课章节目录
