2023年中考数学三轮冲刺复习——二次函数应用01(无答案)
文档属性
| 名称 | 2023年中考数学三轮冲刺复习——二次函数应用01(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:50:28 | ||
图片预览


文档简介
2023中考数学三轮冲刺复习——二次函数应用01
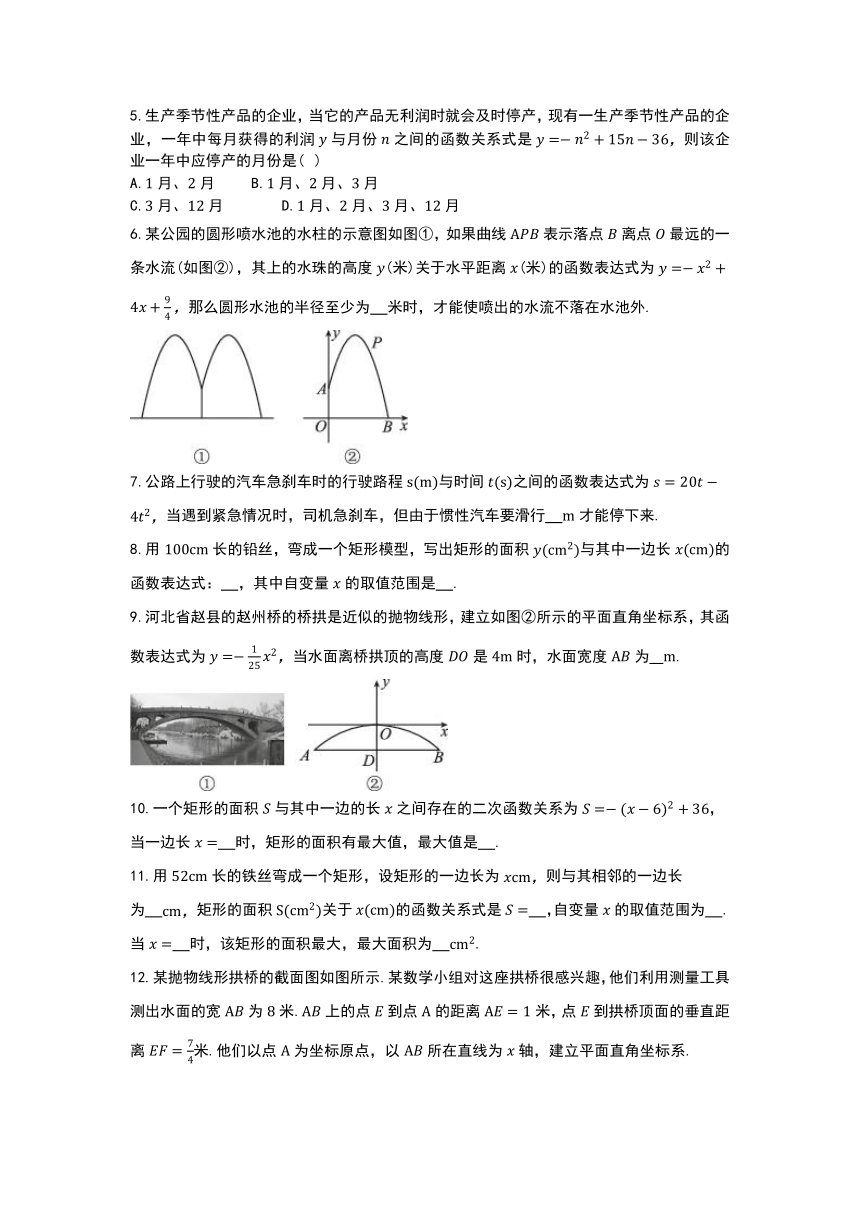
1.如图,在长为30米、宽为20米的矩形花坛中横向修建1条、纵向修建2条宽都为x米的小路(阴影部分),空白处为绿地,面积为y平方米,则绿地面积y与x之间的函数表达式为( )
A. B.
C. D.
2.矩形的长为5,宽为3,如果长和宽都增加x,那么面积增加y,则y与x之间的函数表达式是( )
A. B.
C. D.
3.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放辆单车,设该公司第二、三两个月投放单车数量的月平均增长率为,那么与之间的函数表达式为( )
A. B.
C. D.
4.用总长为的材料做成如图①所示的矩形窗框,设窗框的宽为窗框的面积为关于的函数图象如图②所示,则的值是( )
A. B. C. D.
5.生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,一年中每月获得的利润与月份之间的函数关系式是则该企业一年中应停产的月份是( )
A.月、月 B.月、月、月
C.月、月 D.月、月、月、月
6.某公园的圆形喷水池的水柱的示意图如图①,如果曲线表示落点离点最远的一条水流(如图②),其上的水珠的高度(米)关于水平距离(米)的函数表达式为那么圆形水池的半径至少为 米时,才能使喷出的水流不落在水池外.
7.公路上行驶的汽车急刹车时的行驶路程与时间之间的函数表达式为当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 才能停下来.
8.用长的铅丝,弯成一个矩形模型,写出矩形的面积与其中一边长的函数表达式: ,其中自变量的取值范围是 .
9.河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图②所示的平面直角坐标系,其函数表达式为当水面离桥拱顶的高度是时,水面宽度为 .
10.一个矩形的面积与其中一边的长之间存在的二次函数关系为,当一边长 时,矩形的面积有最大值,最大值是 .
11.用长的铁丝弯成一个矩形,设矩形的一边长为则与其相邻的一边长为 矩形的面积关于的函数关系式是 ,自变量的取值范围为 .当 时,该矩形的面积最大,最大面积为 .
12.某抛物线形拱桥的截面图如图所示.某数学小组对这座拱桥很感兴趣,他们利用测量工具测出水面的宽为米.上的点到点的距离米,点到拱桥顶面的垂直距离米.他们以点为坐标原点,以所在直线为轴,建立平面直角坐标系.
(1)求该抛物线所对应的函数解析式;
(2)求拱桥顶面离水面的最大高度;
(3)现有一游船(截面为矩形)宽度为米,船顶到水面的高度为米.要求游船从拱桥下面正中间通过时,船顶到拱桥顶面的距离应大于米.请通过计算说明该游船是否能安全通过.
13.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫降价元,商场平均每天可多售出件.
(1)若商场平均每天销售这种衬衫的盈利要达到元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天的盈利最多?最多为多少元?
14.一种进价为每件元的上衣,若销售单价为元时,则每周可卖出件.为提高利润,对该种上衣进行涨价销售,经过调查发现,每涨价元,每周要少卖出件,请确定该种上衣涨价后每周销售利润(元)与销售单价(元)之间的函数关系式,并求出当销售单价定为多少元时,每周的销售利润最大,最大值为多少.
15.某货车销售公司,分别试销售两种型号的货车各一个月,并从中选择一种长期销售,设每月销售量为台.若销售甲型货车,每月的销售利润为(万元).已知每台货车的利润为
万元是常数,每月还需支出杂费及其他费用万元,受条件限制每月最多能销售甲型货车辆;若销售乙型货车,每月的销售利润(万元)与之间的函数解析式为且当时当时受条件限制每月最多能销售乙型货车辆.
(1)分别求出与之间的函数解析式;
(2)若求的值;
(3)分别求出销售这两种货车的最大月利润;
(4)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
16.如图,抛物线过点交轴于点是该抛物线上一动点,点从点沿抛物线向点运动(点不与点重合),过点作轴交直线于点.
(1)求抛物线的解析式.
(2)当点在线段上运动时,求点在运动的过程中线段长度的最大值.
(3)在抛物线的对称轴上是否存在点使的值最大?若存在,请求出点的坐标;若不存在,请说明理由.
17.如图,在平面直角坐标系中,已知抛物线经过两点,与轴交于点.
(1)求抛物线的解析式;
(2)若为第三象限内抛物线上一动点,点的横坐标为的面积为求关于的函数解析式,并求出的最大值.
18.如图,以的速度将小球沿与地面成角的方向击出时,球的飞行路线将是一条抛物线.球的飞行高度关于飞行时间的函数表达式为.
(1)小球的飞行高度能否达到?如果能,请求出飞行时间;
(2)小球从飞出到落地要用多少时间?
19.安徽亳州是全球最大的中药材集散中心和价格形成中心,经销商老板按照现在的市场价格购进黄连存放在通风、阴凉、干燥的仓库中,下面是该老板和他的助手小度的对话:
老板:“这些黄连存放在仓库中,每天需要支出各种费用共计元,而且平均每天将会有的损耗”
小度:“黄连现在的市场价格为元经调查,黄连市场价格每天每千克将上涨元”.
若存放天后,将这些黄连一次性售出,设这些黄连的销售总金额为元,获得的利润为元(利润=销售总金额-收购成本-各种费用).经测算,当时.
(1)求的值及与之间的函数表达式;
(2)这些黄连存放多少天出售,获得的利润最大?最大利润是多少?
20.某房地产开发公司于年月份完工一商品房小区月初开始销售,其中月的销售单价为万元月的销售单价为万元且每月的销售单价(单位:万元与月份为整数)之间满足一次函数关系,每月的销售面积为(单位:其中为整数).
(1)求与月份之间的函数解析式;
(2)~月中,哪个月的销售额最高?最高销售额为多少万元?
(3)年月时,因政策的影响,该公司销售部预计月份的销售面积会在月销售面积的基础上减少于是决定将月的销售单价在月的基础上增加该计划顺利完成.为了尽快收回资金年月公司进行降价促销,该月销售额为万元.这样月、月的销售额共有万元,请根据以上条件判断的值是否存在,若存在,请求出的值
21.如图,抛物线与直线相交于点且这条抛物线的对称轴为直线.
(1)若将该抛物线平移使得其经过原点,且对称轴不变,求平移后的抛物线的解析式及的值;
(2)设为直线下方的抛物线上一点,连接求面积的最大值及此时点的坐标.
1.如图,在长为30米、宽为20米的矩形花坛中横向修建1条、纵向修建2条宽都为x米的小路(阴影部分),空白处为绿地,面积为y平方米,则绿地面积y与x之间的函数表达式为( )
A. B.
C. D.
2.矩形的长为5,宽为3,如果长和宽都增加x,那么面积增加y,则y与x之间的函数表达式是( )
A. B.
C. D.
3.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放辆单车,设该公司第二、三两个月投放单车数量的月平均增长率为,那么与之间的函数表达式为( )
A. B.
C. D.
4.用总长为的材料做成如图①所示的矩形窗框,设窗框的宽为窗框的面积为关于的函数图象如图②所示,则的值是( )
A. B. C. D.
5.生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,一年中每月获得的利润与月份之间的函数关系式是则该企业一年中应停产的月份是( )
A.月、月 B.月、月、月
C.月、月 D.月、月、月、月
6.某公园的圆形喷水池的水柱的示意图如图①,如果曲线表示落点离点最远的一条水流(如图②),其上的水珠的高度(米)关于水平距离(米)的函数表达式为那么圆形水池的半径至少为 米时,才能使喷出的水流不落在水池外.
7.公路上行驶的汽车急刹车时的行驶路程与时间之间的函数表达式为当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 才能停下来.
8.用长的铅丝,弯成一个矩形模型,写出矩形的面积与其中一边长的函数表达式: ,其中自变量的取值范围是 .
9.河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图②所示的平面直角坐标系,其函数表达式为当水面离桥拱顶的高度是时,水面宽度为 .
10.一个矩形的面积与其中一边的长之间存在的二次函数关系为,当一边长 时,矩形的面积有最大值,最大值是 .
11.用长的铁丝弯成一个矩形,设矩形的一边长为则与其相邻的一边长为 矩形的面积关于的函数关系式是 ,自变量的取值范围为 .当 时,该矩形的面积最大,最大面积为 .
12.某抛物线形拱桥的截面图如图所示.某数学小组对这座拱桥很感兴趣,他们利用测量工具测出水面的宽为米.上的点到点的距离米,点到拱桥顶面的垂直距离米.他们以点为坐标原点,以所在直线为轴,建立平面直角坐标系.
(1)求该抛物线所对应的函数解析式;
(2)求拱桥顶面离水面的最大高度;
(3)现有一游船(截面为矩形)宽度为米,船顶到水面的高度为米.要求游船从拱桥下面正中间通过时,船顶到拱桥顶面的距离应大于米.请通过计算说明该游船是否能安全通过.
13.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫降价元,商场平均每天可多售出件.
(1)若商场平均每天销售这种衬衫的盈利要达到元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天的盈利最多?最多为多少元?
14.一种进价为每件元的上衣,若销售单价为元时,则每周可卖出件.为提高利润,对该种上衣进行涨价销售,经过调查发现,每涨价元,每周要少卖出件,请确定该种上衣涨价后每周销售利润(元)与销售单价(元)之间的函数关系式,并求出当销售单价定为多少元时,每周的销售利润最大,最大值为多少.
15.某货车销售公司,分别试销售两种型号的货车各一个月,并从中选择一种长期销售,设每月销售量为台.若销售甲型货车,每月的销售利润为(万元).已知每台货车的利润为
万元是常数,每月还需支出杂费及其他费用万元,受条件限制每月最多能销售甲型货车辆;若销售乙型货车,每月的销售利润(万元)与之间的函数解析式为且当时当时受条件限制每月最多能销售乙型货车辆.
(1)分别求出与之间的函数解析式;
(2)若求的值;
(3)分别求出销售这两种货车的最大月利润;
(4)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
16.如图,抛物线过点交轴于点是该抛物线上一动点,点从点沿抛物线向点运动(点不与点重合),过点作轴交直线于点.
(1)求抛物线的解析式.
(2)当点在线段上运动时,求点在运动的过程中线段长度的最大值.
(3)在抛物线的对称轴上是否存在点使的值最大?若存在,请求出点的坐标;若不存在,请说明理由.
17.如图,在平面直角坐标系中,已知抛物线经过两点,与轴交于点.
(1)求抛物线的解析式;
(2)若为第三象限内抛物线上一动点,点的横坐标为的面积为求关于的函数解析式,并求出的最大值.
18.如图,以的速度将小球沿与地面成角的方向击出时,球的飞行路线将是一条抛物线.球的飞行高度关于飞行时间的函数表达式为.
(1)小球的飞行高度能否达到?如果能,请求出飞行时间;
(2)小球从飞出到落地要用多少时间?
19.安徽亳州是全球最大的中药材集散中心和价格形成中心,经销商老板按照现在的市场价格购进黄连存放在通风、阴凉、干燥的仓库中,下面是该老板和他的助手小度的对话:
老板:“这些黄连存放在仓库中,每天需要支出各种费用共计元,而且平均每天将会有的损耗”
小度:“黄连现在的市场价格为元经调查,黄连市场价格每天每千克将上涨元”.
若存放天后,将这些黄连一次性售出,设这些黄连的销售总金额为元,获得的利润为元(利润=销售总金额-收购成本-各种费用).经测算,当时.
(1)求的值及与之间的函数表达式;
(2)这些黄连存放多少天出售,获得的利润最大?最大利润是多少?
20.某房地产开发公司于年月份完工一商品房小区月初开始销售,其中月的销售单价为万元月的销售单价为万元且每月的销售单价(单位:万元与月份为整数)之间满足一次函数关系,每月的销售面积为(单位:其中为整数).
(1)求与月份之间的函数解析式;
(2)~月中,哪个月的销售额最高?最高销售额为多少万元?
(3)年月时,因政策的影响,该公司销售部预计月份的销售面积会在月销售面积的基础上减少于是决定将月的销售单价在月的基础上增加该计划顺利完成.为了尽快收回资金年月公司进行降价促销,该月销售额为万元.这样月、月的销售额共有万元,请根据以上条件判断的值是否存在,若存在,请求出的值
21.如图,抛物线与直线相交于点且这条抛物线的对称轴为直线.
(1)若将该抛物线平移使得其经过原点,且对称轴不变,求平移后的抛物线的解析式及的值;
(2)设为直线下方的抛物线上一点,连接求面积的最大值及此时点的坐标.
同课章节目录
