2023年中考数学高频考点专题复习-销售问题(实际问题与二次函数)(含答案)
文档属性
| 名称 | 2023年中考数学高频考点专题复习-销售问题(实际问题与二次函数)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:50:49 | ||
图片预览



文档简介
2023年中考数学高频考点专题复习-销售问题(实际问题与二次函数)
1.某市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积(单位:百万平方米),与时间x的关系是,(单位:年, 且x为整数);后4年,每年竣工投入使用的公租房面积(单位:百万平方米),与时间x的关系是,(单位:年, 且x为整数)假设每年的公租房全部出租完另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金(单位:元)与时间(单位:年, 且x为整数)满足一次函数关系如下表:
(元) 50 52 54 56 58
(年) 1 2 3 4 5
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高,这样可解决住房的人数将比第6年减少,求a的值.(参考数据:)
2.某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
3.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x
(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
4.我市某乡镇在农业产业合作化销售中,其中一农产品经分析发现月销售量y(万件)与月份x(月)的关系为:,每件产品的利润z(元)与月份x(月)的关系如下表:
x 1 2 3 4 5 6 7 8 9 10 11 12
z 19 18 17 16 15 14 13 12 11 10 9 8
(1)请你根据表格求出每件产品利润(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
5.红灯笼,象征着国家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,若规定每对乙灯笼的利润不能高于30元,设乙灯笼每对售价为元,小明一天通过乙灯笼获得利润元.
①求出与之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
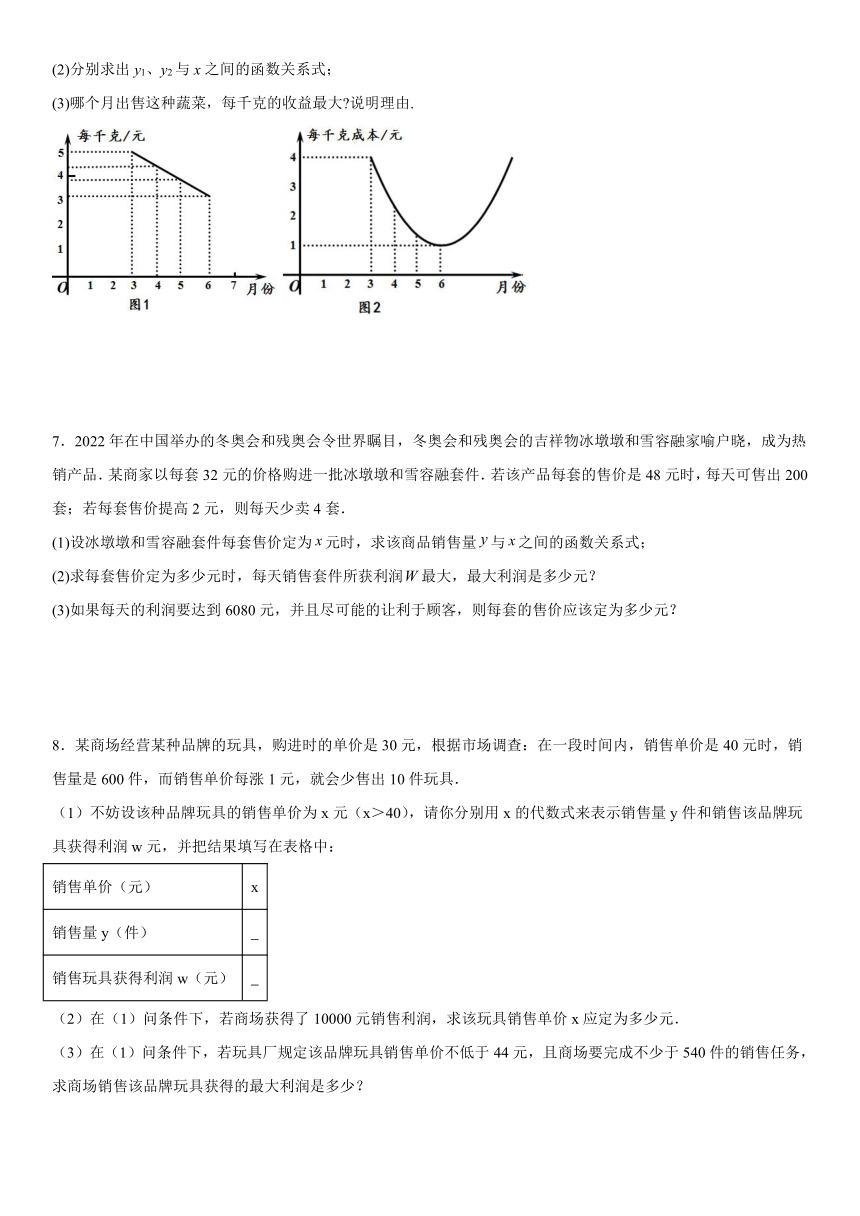
6.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元 (收益=售价-成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大 说明理由.
7.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套32元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为元时,求该商品销售量与之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润最大,最大利润是多少元?
(3)如果每天的利润要达到6080元,并且尽可能的让利于顾客,则每套的售价应该定为多少元?
8.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) x
销售量y(件)
销售玩具获得利润w(元)
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
9.某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) … 5 10 15 20 …
y(元/件) … 75 70 65 60 …
(1)由题意知商品的最低销售单价是 元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
10.某种植基地种植一种蔬菜,它的成本是每千克2元,售价是每千克3元,年销量为10(万千克).基地准备拿出一定的资金作绿色开发,若每年绿色开发投入的资金为(万元),该种蔬菜的年销量将是原年销量的倍,与的关系如下表:
(万元) 0 1 2 3 4 5 …
1 1.5 1.8 1.9 1.8 1.5 …
(1)猜想与之间的函数类型是_______函数,求出该函数的表达式为_______;
(2)求年利润(万元) 与绿色开发投入的资金(万元)之间的函数关系式;当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润(万元)的最大值;(注:年利润=销售总额-成本费-绿色开发投入的资金);
(3)若提高种植人员的奖金,发现又增加一部分年销量,经调查发现:再次增加的年销量(万千克)与每年提高种植人员的奖金(万元)之间满足,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(,结果精确到0.1万元).
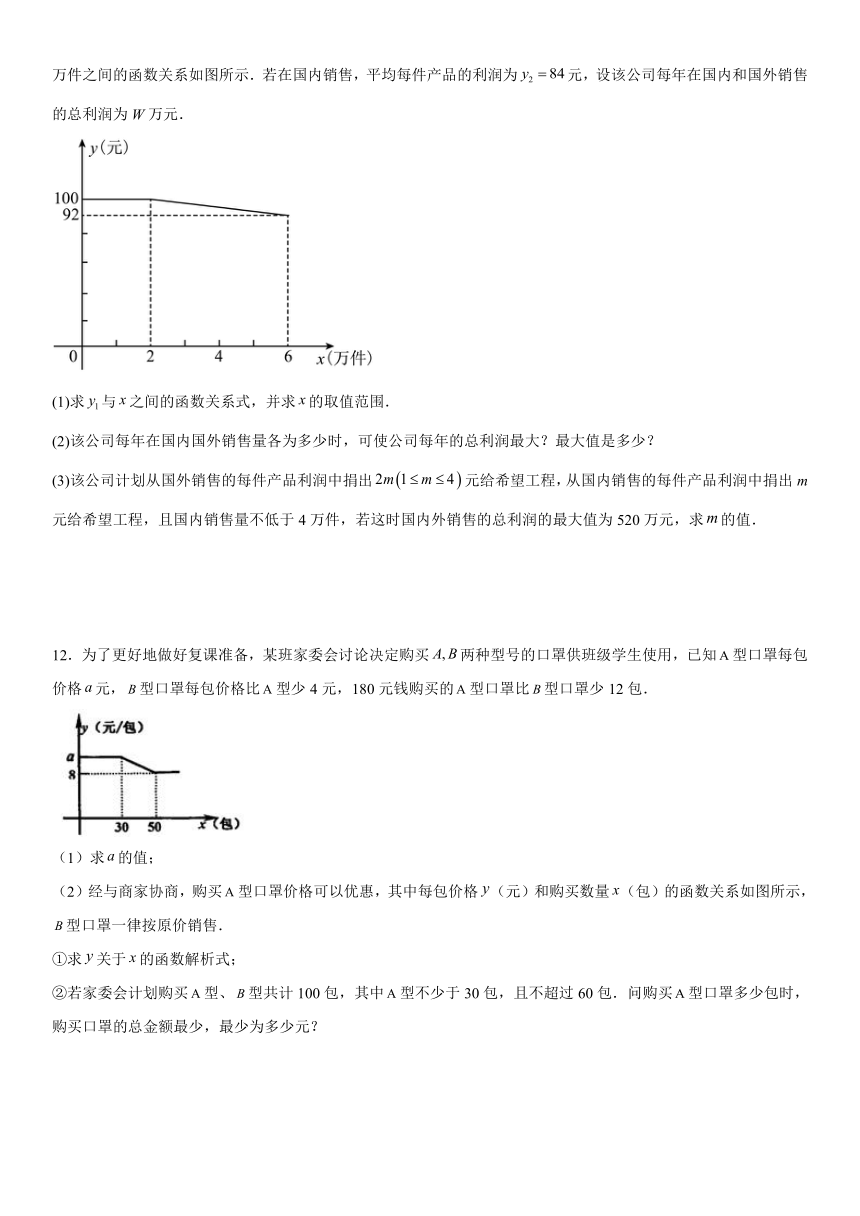
11.某公司生产的一种产品在市场上很受欢迎,该公司每年的产量为6万件,可在国内和国外两个市场全部销售.若在国外销售,平均每件产品的利润元与国外销售量x
万件之间的函数关系如图所示.若在国内销售,平均每件产品的利润为元,设该公司每年在国内和国外销售的总利润为W万元.
(1)求与之间的函数关系式,并求的取值范围.
(2)该公司每年在国内国外销售量各为多少时,可使公司每年的总利润最大?最大值是多少?
(3)该公司计划从国外销售的每件产品利润中捐出元给希望工程,从国内销售的每件产品利润中捐出m元给希望工程,且国内销售量不低于4万件,若这时国内外销售的总利润的最大值为520万元,求的值.
12.为了更好地做好复课准备,某班家委会讨论决定购买两种型号的口罩供班级学生使用,已知型口罩每包价格元,型口罩每包价格比型少4元,180元钱购买的型口罩比型口罩少12包.
(1)求的值;
(2)经与商家协商,购买型口罩价格可以优惠,其中每包价格(元)和购买数量(包)的函数关系如图所示,型口罩一律按原价销售.
①求关于的函数解析式;
②若家委会计划购买型、型共计100包,其中型不少于30包,且不超过60包.问购买型口罩多少包时,购买口罩的总金额最少,最少为多少元?
13.某塑料厂生产一种家用塑料制品,它的成本是元件,售价是元件,年销售量为
万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费万元,产品的年销售量将是原销售量的倍,且与之间满足,具体数量如下表:
(万元)
(1)求与的函数关系式(不要求写出自变量的取值范围);
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润(万元)与广告费用(万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(3)如果厂家希望年利润(万元)不低于万元,请你帮助厂家确定广告费的范围.
14.某经销商在市场价格为元/千克时收购了某种有机蔬菜千克存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨元,但冷库存放这批蔬菜时每天需要支出各种费用合计元,已知这种蔬菜在冷库中最多保存天,同时,平均每天将会有千克的蔬菜损坏不能出售.
(1)若存放天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为元,试写出与之间的函数关系式.
(2)经销商想获得利润元,设将这批蔬菜存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少?
15.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为元/件,每天销售(件)与销售单价(元)之间存在一次函数关系,如图所示.
(1)求与之间的函数关系;
(2)如果规定每天漆器笔筒的销售量不低于件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于元,试确定该漆器笔筒销售单价的范围.
16.为满足市场需求,新生活超市在端午节前夕购进价格为元/个的粽子,根据市场预测,该品牌粽子每个售价元时,每天能出售个,并且售价每上涨元,其销售量将减少个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的.
(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为元.
(2)定价为多少时每天的利润最大?最大利润是多少?
17.“水都数学建模”兴趣小组对某超市一种热卖的商品做了市场调查,发现该商品的进价为每件30元,开始到3月底的一段时间,超市以每件40元售出,每天可以卖出120件.从4月1日开始,该商品每天比前一天涨价1元,销售量每天比前一天减少2件;从5月1日起到5月30日当天,该商品价格一直稳定在每件70元,销售量一直持续每天比前一天减少2件,设从4月1日起的第x天的销售量为y元,销售该商品的每天利润为w元.
(1)第天的销售价为每件_______元,这段时间每天的销售量y(元)与x(天)的函数关系式为__________;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2000元?
参考答案:
1.(1)(2)第3年收取的租金最多,最多为243百万元;(3)a的值为20.
2.(1)y=50-,且0≤x≤160,且x为10的正整数倍.(2)w=-x2+34x+8000;(3)一天订住34个房间时,宾馆每天利润最大,最大利润为10880元.
3.(1)600元;(2)当销售单价定为30元时,每月可获得最大利润4000;(3)销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
4.(1) z=﹣x+20; (2) (x均为整数)(3)当x=8时,w取最大值,最大值为144万元
5.(1)甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对;
(2)①,②乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.
6.(1)6月份出售这种蔬菜每千克的收益是2元.(2)y1=﹣+7;y2=x2﹣4x+13.(3)5月份出售这种蔬菜,每千克的收益最大.
7.(1)
(2)当时,;
(3)每套的售价应该定为72元.
8.(1) 1000﹣x,﹣10x2+1300x﹣30000;(2)50元或80元;(3)8640元.
9.(1)50,y=﹣x+80(0≤x≤30,且x为正整数);(2)当销售单价为60元时,所获利润最大,最大利润为400元.
10.(1)二次,;(2)年利润(万元)的最大值为16万元;(3)用于绿色开发的资金为3.7万元,奖金为1.3万元.
11.(1)
(2)当该公司每年的国外销售量为5万件,国内销售量为1万件时,可使公司每年的总利润最大,最大值是554万元
(3)2
12.(1);(2)①当时,;当时,;当时,;②当购买型口罩50包时,购买口罩的总金额最少,最少为700元
13.(1);(2)年利润(万元)与广告费用(万元)的函数关系式为,每年投入的广告费是万元时,所获得的利润最大,为万元;(3)当时,年利润(万元)不低于万元.
14.(1)
(2)天
(3)存放天后出售这批蔬菜可获得最大利润元
15.(1);(2)销售单价为44元时,每天获取的利润最大,元;(3).
16.(1)定价为元时,每天的利润为元;(2)当定价为元时,每天的利润最大,最大的利润是元.
17.(1)(x+40);
(2)销售该商品第25天时,当天销售利润最大,最大利润是240元;
(3)该商品在销售过程中,共有26天每天销售利润不低于2000元;
1.某市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积(单位:百万平方米),与时间x的关系是,(单位:年, 且x为整数);后4年,每年竣工投入使用的公租房面积(单位:百万平方米),与时间x的关系是,(单位:年, 且x为整数)假设每年的公租房全部出租完另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金(单位:元)与时间(单位:年, 且x为整数)满足一次函数关系如下表:
(元) 50 52 54 56 58
(年) 1 2 3 4 5
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高,这样可解决住房的人数将比第6年减少,求a的值.(参考数据:)
2.某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
3.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x
(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
4.我市某乡镇在农业产业合作化销售中,其中一农产品经分析发现月销售量y(万件)与月份x(月)的关系为:,每件产品的利润z(元)与月份x(月)的关系如下表:
x 1 2 3 4 5 6 7 8 9 10 11 12
z 19 18 17 16 15 14 13 12 11 10 9 8
(1)请你根据表格求出每件产品利润(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
5.红灯笼,象征着国家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,若规定每对乙灯笼的利润不能高于30元,设乙灯笼每对售价为元,小明一天通过乙灯笼获得利润元.
①求出与之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
6.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元 (收益=售价-成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大 说明理由.
7.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套32元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为元时,求该商品销售量与之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润最大,最大利润是多少元?
(3)如果每天的利润要达到6080元,并且尽可能的让利于顾客,则每套的售价应该定为多少元?
8.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) x
销售量y(件)
销售玩具获得利润w(元)
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
9.某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) … 5 10 15 20 …
y(元/件) … 75 70 65 60 …
(1)由题意知商品的最低销售单价是 元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
10.某种植基地种植一种蔬菜,它的成本是每千克2元,售价是每千克3元,年销量为10(万千克).基地准备拿出一定的资金作绿色开发,若每年绿色开发投入的资金为(万元),该种蔬菜的年销量将是原年销量的倍,与的关系如下表:
(万元) 0 1 2 3 4 5 …
1 1.5 1.8 1.9 1.8 1.5 …
(1)猜想与之间的函数类型是_______函数,求出该函数的表达式为_______;
(2)求年利润(万元) 与绿色开发投入的资金(万元)之间的函数关系式;当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润(万元)的最大值;(注:年利润=销售总额-成本费-绿色开发投入的资金);
(3)若提高种植人员的奖金,发现又增加一部分年销量,经调查发现:再次增加的年销量(万千克)与每年提高种植人员的奖金(万元)之间满足,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(,结果精确到0.1万元).
11.某公司生产的一种产品在市场上很受欢迎,该公司每年的产量为6万件,可在国内和国外两个市场全部销售.若在国外销售,平均每件产品的利润元与国外销售量x
万件之间的函数关系如图所示.若在国内销售,平均每件产品的利润为元,设该公司每年在国内和国外销售的总利润为W万元.
(1)求与之间的函数关系式,并求的取值范围.
(2)该公司每年在国内国外销售量各为多少时,可使公司每年的总利润最大?最大值是多少?
(3)该公司计划从国外销售的每件产品利润中捐出元给希望工程,从国内销售的每件产品利润中捐出m元给希望工程,且国内销售量不低于4万件,若这时国内外销售的总利润的最大值为520万元,求的值.
12.为了更好地做好复课准备,某班家委会讨论决定购买两种型号的口罩供班级学生使用,已知型口罩每包价格元,型口罩每包价格比型少4元,180元钱购买的型口罩比型口罩少12包.
(1)求的值;
(2)经与商家协商,购买型口罩价格可以优惠,其中每包价格(元)和购买数量(包)的函数关系如图所示,型口罩一律按原价销售.
①求关于的函数解析式;
②若家委会计划购买型、型共计100包,其中型不少于30包,且不超过60包.问购买型口罩多少包时,购买口罩的总金额最少,最少为多少元?
13.某塑料厂生产一种家用塑料制品,它的成本是元件,售价是元件,年销售量为
万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费万元,产品的年销售量将是原销售量的倍,且与之间满足,具体数量如下表:
(万元)
(1)求与的函数关系式(不要求写出自变量的取值范围);
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润(万元)与广告费用(万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(3)如果厂家希望年利润(万元)不低于万元,请你帮助厂家确定广告费的范围.
14.某经销商在市场价格为元/千克时收购了某种有机蔬菜千克存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨元,但冷库存放这批蔬菜时每天需要支出各种费用合计元,已知这种蔬菜在冷库中最多保存天,同时,平均每天将会有千克的蔬菜损坏不能出售.
(1)若存放天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为元,试写出与之间的函数关系式.
(2)经销商想获得利润元,设将这批蔬菜存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少?
15.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为元/件,每天销售(件)与销售单价(元)之间存在一次函数关系,如图所示.
(1)求与之间的函数关系;
(2)如果规定每天漆器笔筒的销售量不低于件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于元,试确定该漆器笔筒销售单价的范围.
16.为满足市场需求,新生活超市在端午节前夕购进价格为元/个的粽子,根据市场预测,该品牌粽子每个售价元时,每天能出售个,并且售价每上涨元,其销售量将减少个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的.
(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为元.
(2)定价为多少时每天的利润最大?最大利润是多少?
17.“水都数学建模”兴趣小组对某超市一种热卖的商品做了市场调查,发现该商品的进价为每件30元,开始到3月底的一段时间,超市以每件40元售出,每天可以卖出120件.从4月1日开始,该商品每天比前一天涨价1元,销售量每天比前一天减少2件;从5月1日起到5月30日当天,该商品价格一直稳定在每件70元,销售量一直持续每天比前一天减少2件,设从4月1日起的第x天的销售量为y元,销售该商品的每天利润为w元.
(1)第天的销售价为每件_______元,这段时间每天的销售量y(元)与x(天)的函数关系式为__________;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2000元?
参考答案:
1.(1)(2)第3年收取的租金最多,最多为243百万元;(3)a的值为20.
2.(1)y=50-,且0≤x≤160,且x为10的正整数倍.(2)w=-x2+34x+8000;(3)一天订住34个房间时,宾馆每天利润最大,最大利润为10880元.
3.(1)600元;(2)当销售单价定为30元时,每月可获得最大利润4000;(3)销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
4.(1) z=﹣x+20; (2) (x均为整数)(3)当x=8时,w取最大值,最大值为144万元
5.(1)甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对;
(2)①,②乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.
6.(1)6月份出售这种蔬菜每千克的收益是2元.(2)y1=﹣+7;y2=x2﹣4x+13.(3)5月份出售这种蔬菜,每千克的收益最大.
7.(1)
(2)当时,;
(3)每套的售价应该定为72元.
8.(1) 1000﹣x,﹣10x2+1300x﹣30000;(2)50元或80元;(3)8640元.
9.(1)50,y=﹣x+80(0≤x≤30,且x为正整数);(2)当销售单价为60元时,所获利润最大,最大利润为400元.
10.(1)二次,;(2)年利润(万元)的最大值为16万元;(3)用于绿色开发的资金为3.7万元,奖金为1.3万元.
11.(1)
(2)当该公司每年的国外销售量为5万件,国内销售量为1万件时,可使公司每年的总利润最大,最大值是554万元
(3)2
12.(1);(2)①当时,;当时,;当时,;②当购买型口罩50包时,购买口罩的总金额最少,最少为700元
13.(1);(2)年利润(万元)与广告费用(万元)的函数关系式为,每年投入的广告费是万元时,所获得的利润最大,为万元;(3)当时,年利润(万元)不低于万元.
14.(1)
(2)天
(3)存放天后出售这批蔬菜可获得最大利润元
15.(1);(2)销售单价为44元时,每天获取的利润最大,元;(3).
16.(1)定价为元时,每天的利润为元;(2)当定价为元时,每天的利润最大,最大的利润是元.
17.(1)(x+40);
(2)销售该商品第25天时,当天销售利润最大,最大利润是240元;
(3)该商品在销售过程中,共有26天每天销售利润不低于2000元;
同课章节目录
