2023年山东省济南市莱芜区初中数学中考模拟冲刺卷(二)(含答案)
文档属性
| 名称 | 2023年山东省济南市莱芜区初中数学中考模拟冲刺卷(二)(含答案) | 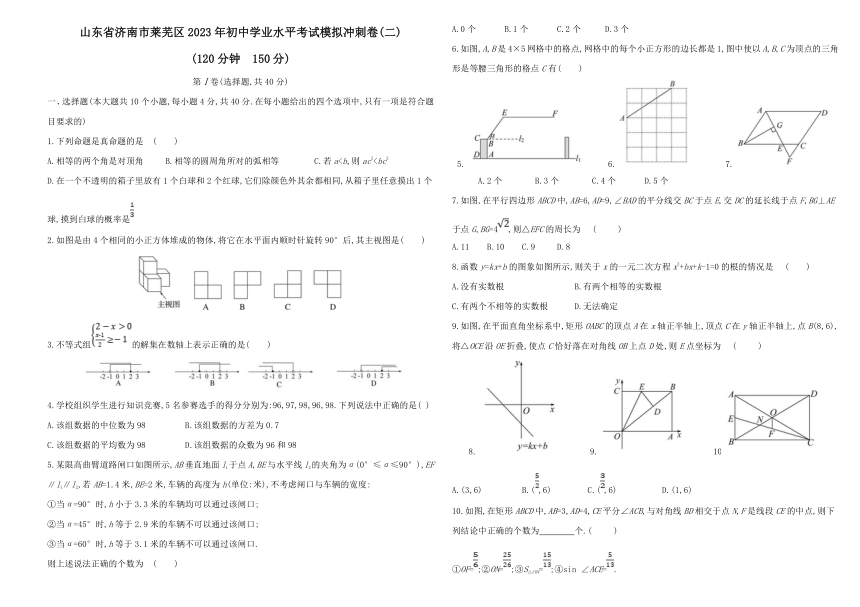 | |
| 格式 | docx | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 23:54:41 | ||
图片预览




文档简介
山东省济南市莱芜区2023年初中学业水平考试模拟冲刺卷(二)
(120分钟 150分)
第Ⅰ卷(选择题,共40分)
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列命题是真命题的是 ( )
A.相等的两个角是对顶角 B.相等的圆周角所对的弧相等 C.若aD.在一个不透明的箱子里放有1个白球和2个红球,它们除颜色外其余都相同,从箱子里任意摸出1个球,摸到白球的概率是
2.如图是由4个相同的小正方体堆成的物体,将它在水平面内顺时针旋转90°后,其主视图是( )
3.不等式组的解集在数轴上表示正确的是( )
4.学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是( )
A.该组数据的中位数为98 B.该组数据的方差为0.7
C.该组数据的平均数为98 D.该组数据的众数为96和98
5.某限高曲臂道路闸口如图所示,AB垂直地面l1于点A,BE与水平线l2的夹角为α(0°≤α≤90°),EF∥l1∥l2,若AB=1.4米,BE=2米,车辆的高度为h(单位:米),不考虑闸口与车辆的宽度:
①当α=90°时,h小于3.3米的车辆均可以通过该闸口;
②当α=45°时,h等于2.9米的车辆不可以通过该闸口;
③当α=60°时,h等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为 ( )
A.0个 B.1个 C.2个 D.3个
6.如图,A,B是4×5网格中的格点,网格中的每个小正方形的边长都是1,图中使以A,B,C为顶点的三角形是等腰三角形的格点C有( )
5. 6. 7.
A.2个 B.3个 C.4个 D.5个
7.如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4,则△EFC的周长为 ( )
A.11 B.10 C.9 D.8
8.函数y=kx+b的图象如图所示,则关于x的一元二次方程x2+bx+k-1=0的根的情况是 ( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.无法确定
9.如图,在平面直角坐标系中,矩形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,点B(8,6),将△OCE沿OE折叠,使点C恰好落在对角线OB上点D处,则E点坐标为 ( )
8. 9. 10
A.(3,6) B.(,6) C.(,6) D.(1,6)
10.如图,在矩形ABCD中,AB=3,AD=4,CE平分∠ACB,与对角线BD相交于点N,F是线段CE的中点,则下列结论中正确的个数为 个.( )
①OF=;②ON=;③S△CON=;④sin ∠ACE=.
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题,共110分)
二、填空题(本大题共6个小题,每小题4分,满分24分.直接填写最后结果)
11.因式分解:x3-2x2-3x= .
12.若(2x+y-5)2+=0,则x-y的值是 .
13.如图,扇形圆心角为60°,半径为4,点E,F分别为OA,OB的中点,连接BE与AF相交于点G,则阴影部分的面积为 .
14.已知正多边形的一个外角等于40°,则这个正多边形的内角和的度数为 .
15.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 (填序号).
13. 15. 16.
16.如图,抛物线y=-x2-6x-5交x轴于A,B两点,交y轴于点C,点D(m,m+1)是抛物线上的点,则点D关于直线AC的对称点的坐标为 .
三、解答题(本大题共10小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
17.(6分)计算:.
18.(6分)解不等式组,并将解集表示在所给的数轴上.
19.(6分)如图,已知平行四边形ABCD中,F,G是AB边上的两个点,且FC平分∠BCD,GD平分∠ADC,FC与GD相交于点E,求证:AF=GB.
20.(8分)2022年4月29日,湖北日报联合夏风教室发起“劳动最光荣,加油好少年”主题活动.某校学生积极参与本次主题活动,为了解该校学生参与本次主题活动的情况,随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图(如图).请结合图中信息解答下列问题:
(1)本次共调查了 名学生,并补全条形统计图;
(2)若该校共有1 200名学生参加本次主题活动,则本次活动中该校“洗衣服”的学生约有多少名
(3)现从参与本次主题活动的甲、乙、丙、丁4名学生中,随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法,求甲、乙两人同时被抽中的概率.
21.(8分)我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”(如图①).数学兴趣小组利用无人机测量古槐的高度,如图②所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米E点处时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B与树底D的水平距离为20米,求古槐的高度(结果精确到1米).
(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50,sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
22.(8分)如图,在矩形ABCD中,E是AB上一点,连接CE,以CE为直径的☉O与AD边交于点F,交CD于点G,连接OF,GF,EF,若∠BEC=∠CEF=60°,AF=2.
(1)试判断☉O与AD的位置关系,并说明理由;
(2)求矩形ABCD的周长;
(3)求阴影部分的面积.
23.(10分)为全面贯彻党的教育方针,严格落实教育部对中小学生“五项管理”的相关要求和《关于进一步加强中小学生体质健康管理工作的通知》精神,保障学生每天在校1小时体育活动时间,某班计划采购A,B两种类型的羽毛球拍.已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
(1)求A,B两种类型羽毛球拍的单价;
(2)该班准备采购A,B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.
24.(10分)如图,在平面直角坐标系中,四边形AOBC是矩形,OB=4,OA=3,F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=(k>0)的图象与边AC交于点E.
(1)当BF=BC时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)将△EFC沿EF折叠,得到△EFG,当点G恰好落在矩形AOBC的对角线上时,求k的值.
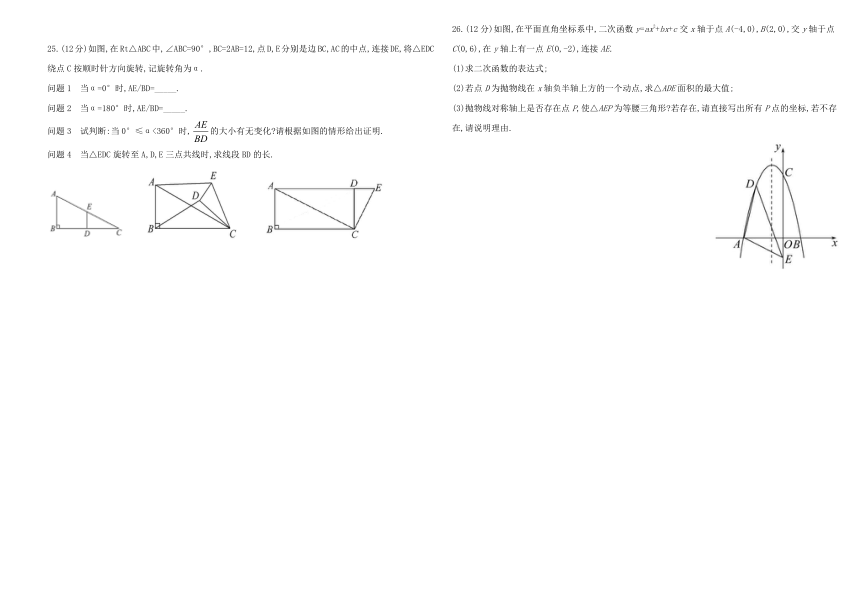
25.(12分)如图,在Rt△ABC中,∠ABC=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题1 当α=0°时,AE/BD=_____.
问题2 当α=180°时,AE/BD=_____.
问题3 试判断:当0°≤α<360°时,的大小有无变化 请根据如图的情形给出证明.
问题4 当△EDC旋转至A,D,E三点共线时,求线段BD的长.
26.(12分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形 若存在,请直接写出所有P点的坐标,若不存在,请说明理由.
山东省济南市莱芜区2023年初中学业水平考试模拟冲刺卷(二)
(120分钟 150分)
第Ⅰ卷(选择题,共40分)
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B D C B D C A C
第Ⅱ卷(非选择题,共110分)
二、填空题(本大题共6个小题,每小题4分,满分24分.直接填写最后结果)
11. x(x-3)(x+1) 12. 9 13. 14. 1 260° 15. ①②③ 16. (-5,-4)或(0,1)
三、解答题(本大题共10小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
17.(6分)计算:(-1)2 021+|-2|+4sin 30°-(√(3&8)-π)0.
【解析】原式=-1+2+4×-1=-1+2+2-1=2.
18.(6分)解不等式组,并将解集表示在所给的数轴上.
【解析】,
解①得:x>2,解②得:x≤4,
故不等式组的解集是:2解集在数轴上表示为
19.(6分)如图,已知平行四边形ABCD中,F,G是AB边上的两个点,且FC平分∠BCD,GD平分∠ADC,FC与GD相交于点E,求证:AF=GB.
【证明】在平行四边形ABCD中,∵DG,CF分别平分∠ADC,∠BCD,
∴∠ADG=∠CDG,∠DCF=∠BCF,
又∵∠CDG=∠AGD,∠DCF=∠BFC,
∴∠ADG=∠AGD,∠BCF=∠BFC,
∴AG=AD,BF=BC,又∵AD=BC,∴AG=BF,
∴AF=GB.
20.(8分)2022年4月29日,湖北日报联合夏风教室发起“劳动最光荣,加油好少年”主题活动.某校学生积极参与本次主题活动,为了解该校学生参与本次主题活动的情况,随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图(如图).请结合图中信息解答下列问题:
(1)本次共调查了 名学生,并补全条形统计图;
(2)若该校共有1 200名学生参加本次主题活动,则本次活动中该校“洗衣服”的学生约有多少名
(3)现从参与本次主题活动的甲、乙、丙、丁4名学生中,随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法,求甲、乙两人同时被抽中的概率.
【解析】(1)40÷20%=200(人),
200-40-50-30-20=60(人),补全条形统计图如图:
答案:200
(2)1 200×=300(人),
答:该校1 200名学生中参与“洗衣服”的学生约有300名;
(3)从甲、乙、丙、丁四个人中选择2个人所有等可能出现的结果情况如表:
第2人 第1人
甲 乙 丙 丁
甲 - 乙甲 丙甲 丁甲
乙 甲乙 - 丙乙 丁乙
丙 甲丙 乙丙 - 丁丙
丁 甲丁 乙丁 丙丁 -
共有12种等可能出现的结果,其中甲、乙同时被抽中的情况有2种,
所以甲、乙同时被抽中的概率为=.
21.(8分)我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”(如图①).数学兴趣小组利用无人机测量古槐的高度,如图②所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米E点处时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B与树底D的水平距离为20米,求古槐的高度(结果精确到1米).
(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50,sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
【解析】过点A作AM⊥EH于M,过点C作CN⊥EH于N,
由题意知,AM=BH,CN=DH,AB=MH,
在Rt△AME中,∠EAM=26.6°,
∴tan∠EAM=EM/AM,
∴AM=EM/tan∠EAM=EH MH/tan26.6°≈45 39/0.5=12(米),∴BH=AM=12米,
∵BD=20,∴DH=BD-BH=8(米),∴CN=8米,
在Rt△ENC中,∠ECN=76°,∴tan∠ECN=EN/CN,
∴EN=CN·tan∠ECN≈8×4.01=32.08(米),
∴CD=NH=EH-EN=12.92≈13(米),
答:古槐的高度约为13米.
22.(8分)如图,在矩形ABCD中,E是AB上一点,连接CE,以CE为直径的☉O与AD边交于点F,交CD于点G,连接OF,GF,EF,若∠BEC=∠CEF=60°,AF=2.
(1)试判断☉O与AD的位置关系,并说明理由;
(2)求矩形ABCD的周长;
(3)求阴影部分的面积.
【解析】(1)☉O与AD相切,
理由:∵四边形ABCD是矩形,∴∠A=90°,
∵∠BEC=∠CEF=60°,
∴∠AEF=180°-∠BEC-∠OEF=60°,∵OF=OE,
∴△OEF是等边三角形,∴∠OFE=60°,∴∠OFE=∠AEF,
∵OF∥AB,∴∠OFA+∠A=180°,∴∠OFA=90°,
∵OF是☉O的半径,∴☉O与AD边相切;
(2)∵四边形ABCD是矩形,∴∠A=∠D=90°,
∴CD⊥AD,BA⊥AD,∴CD∥OF∥AB,∴==1,
∴DF=AF=2,∴AD=4=BC,
∵∠CEB=60°,∠B=90°,∴∠BCE=30°,∴CE=2BE,
∵BC2+BE2=CE2,∴(4)2+BE2=(2BE)2,
∴BE=4,CE=8,
∴OF=OC=OE=4,∠AEF=60°,∠A=90°,AF=2,∴AE=2,
∴CD=AB=6,∴C矩形ABCD=2×(6+4)=12+8;
(3)如图,连接OG,∵CD∥OF∥AB,
∴∠OCG=∠BEC=60°,S△CFG=S△COG,∵OC=OG,
∴△OCG是等边三角形,∴∠COG=60°,
∴S阴影==π.
23.(10分)为全面贯彻党的教育方针,严格落实教育部对中小学生“五项管理”的相关要求和《关于进一步加强中小学生体质健康管理工作的通知》精神,保障学生每天在校1小时体育活动时间,某班计划采购A,B两种类型的羽毛球拍.已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
(1)求A,B两种类型羽毛球拍的单价;
(2)该班准备采购A,B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.
【解析】(1)设A种羽毛球拍每副x元,B种羽毛球拍每副y元,
,解得,
答:A种羽毛球拍每副40元,B种羽毛球拍每副32元.
(2)设购买B种羽毛球拍a副,总费用w元,
依题意得30-a≥2a,解得a≤10,
w=40(30-a)+32a=-8a+1 200,
∵-8<0,∴w随a的增大而减小,
∴当a=10时,w最小,w最小=-8×10+1 200=1 120(元),
此时30-10=20(副),
答:费用最少的方案是购买A种羽毛球拍20副,B种羽毛球拍10副,所需费用1 120元.
24.(10分)如图,在平面直角坐标系中,四边形AOBC是矩形,OB=4,OA=3,F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=(k>0)的图象与边AC交于点E.
(1)当BF=BC时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)将△EFC沿EF折叠,得到△EFG,当点G恰好落在矩形AOBC的对角线上时,求k的值.
【解析】(1)∵OB=4,OA=3,∴点A,B的坐标分别为(0,3),(4,0).∵四边形OACB为矩形,则点C(4,3),
当BF=BC时,点F(4,1),将点F的坐标代入y=,解得:k=4,故反比例函数的表达式为:y=,
当y=3时,x=,故E,3;
(2)∵F点的横坐标为4,点F在反比例函数上,
∴F4,,∴CF=BC-BF=3-=,
∵E的纵坐标为3,∴E,3,
∴CE=AC-AE=4-k=,
在Rt△CEF中,tan ∠EFC==;
(3)①当点G落在对角线AB上时,在Rt△ABC中,tan ∠ABC===tan ∠EFC,
故EF∥AB,
连接CG交EF于点M,则MG=MC,
即点M是CG的中点,而EF∥AB,
故MF是△CGB的中位线,则点F是BC的中点,
故点F的坐标为4,,将点F的坐标代入反比例函数表达式得:k=4×=6;
②当点G落在OC上时,由①知,CG⊥AB,如果G落在OC上,则OC⊥AB,由题意得AB和OC不垂直,
故点G不会落在OC上.综上,k=6.
25.(12分)如图,在Rt△ABC中,∠ABC=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题1 当α=0°时,AE/BD=_____.
问题2 当α=180°时,AE/BD=_____.
问题3 试判断:当0°≤α<360°时,的大小有无变化 请根据如图的情形给出证明.
【解析】当0°≤α<360°时,的大小没有变化.
∵∠ECD=∠ACB,∴∠ECA=∠DCB,
又∵==,∴△ECA∽△DCB,
∴==.
问题4 当△EDC旋转至A,D,E三点共线时,求线段BD的长.
【解析】如图①,当△EDC绕点C顺时针旋转90°时,直线DE经过点A,连接BD.
∵AC=,CD=6,CD⊥AD,
∴AD===12,
∵AD=BC,AB=DC,∴四边形ABCD是平行四边形,
∵∠ABC=90°,∴四边形ABCD是矩形,
∴BD=AC=.
如图②,当△EDC绕点C顺时针旋转至此位置时,直线DE经过点A.连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
∵AC=,CD=6,CD⊥AD,
∴AD==12,
∴AE=AD-DE=12-3=9,
由问题3可得,=,
∴BD==.
综上所述,BD的长为或.
26.(12分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形 若存在,请直接写出所有P点的坐标,若不存在,请说明理由.
【解析】(1)∵二次函数y=ax2+bx+c经过点A(-4,0),B(2,0),C(0,6),
∴解得
所以二次函数的表达式为y=-x2-x+6;
(2)由A(-4,0),E(0,-2),可求AE所在直线表达式为y=-x-2,
过点D作DG⊥x轴于G,交AE于点F,过点E作EH⊥DF,垂足为H,如图.
设Dm,-m2-m+6,则点Fm,-m-2,
∴DF=-m2-m+6--m-2
=-m2-m+8,
∴S△ADE=S△ADF+S△EDF=×DF×AG+DF×EH
=×DF×(AG+EH)=×4×DF
=2×-m2-m+8=-m+2+,
∴当m=-时,△ADE的面积取得最大值为;
(3)y=-x2-x+6的对称轴为x=-1,
设P(-1,n),又E(0,-2),A(-4,0),
可求PA2=9+n2,PE2=1+(n+2)2,AE2=16+4=20,
当PA2=PE2时,9+n2=1+(n+2)2,
解得,n=1,此时P(-1,1);
当PA2=AE2时,9+n2=20,
解得,n=±,此时点P坐标为(-1,±);
当PE2=AE2时,1+(n+2)2=20,
解得,n=-2±,此时点P坐标为:(-1,-2±).
综上所述,P点的坐标为:(-1,1),(-1,±),(-1,-2±).
(120分钟 150分)
第Ⅰ卷(选择题,共40分)
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列命题是真命题的是 ( )
A.相等的两个角是对顶角 B.相等的圆周角所对的弧相等 C.若a
2.如图是由4个相同的小正方体堆成的物体,将它在水平面内顺时针旋转90°后,其主视图是( )
3.不等式组的解集在数轴上表示正确的是( )
4.学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是( )
A.该组数据的中位数为98 B.该组数据的方差为0.7
C.该组数据的平均数为98 D.该组数据的众数为96和98
5.某限高曲臂道路闸口如图所示,AB垂直地面l1于点A,BE与水平线l2的夹角为α(0°≤α≤90°),EF∥l1∥l2,若AB=1.4米,BE=2米,车辆的高度为h(单位:米),不考虑闸口与车辆的宽度:
①当α=90°时,h小于3.3米的车辆均可以通过该闸口;
②当α=45°时,h等于2.9米的车辆不可以通过该闸口;
③当α=60°时,h等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为 ( )
A.0个 B.1个 C.2个 D.3个
6.如图,A,B是4×5网格中的格点,网格中的每个小正方形的边长都是1,图中使以A,B,C为顶点的三角形是等腰三角形的格点C有( )
5. 6. 7.
A.2个 B.3个 C.4个 D.5个
7.如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4,则△EFC的周长为 ( )
A.11 B.10 C.9 D.8
8.函数y=kx+b的图象如图所示,则关于x的一元二次方程x2+bx+k-1=0的根的情况是 ( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.无法确定
9.如图,在平面直角坐标系中,矩形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,点B(8,6),将△OCE沿OE折叠,使点C恰好落在对角线OB上点D处,则E点坐标为 ( )
8. 9. 10
A.(3,6) B.(,6) C.(,6) D.(1,6)
10.如图,在矩形ABCD中,AB=3,AD=4,CE平分∠ACB,与对角线BD相交于点N,F是线段CE的中点,则下列结论中正确的个数为 个.( )
①OF=;②ON=;③S△CON=;④sin ∠ACE=.
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题,共110分)
二、填空题(本大题共6个小题,每小题4分,满分24分.直接填写最后结果)
11.因式分解:x3-2x2-3x= .
12.若(2x+y-5)2+=0,则x-y的值是 .
13.如图,扇形圆心角为60°,半径为4,点E,F分别为OA,OB的中点,连接BE与AF相交于点G,则阴影部分的面积为 .
14.已知正多边形的一个外角等于40°,则这个正多边形的内角和的度数为 .
15.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 (填序号).
13. 15. 16.
16.如图,抛物线y=-x2-6x-5交x轴于A,B两点,交y轴于点C,点D(m,m+1)是抛物线上的点,则点D关于直线AC的对称点的坐标为 .
三、解答题(本大题共10小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
17.(6分)计算:.
18.(6分)解不等式组,并将解集表示在所给的数轴上.
19.(6分)如图,已知平行四边形ABCD中,F,G是AB边上的两个点,且FC平分∠BCD,GD平分∠ADC,FC与GD相交于点E,求证:AF=GB.
20.(8分)2022年4月29日,湖北日报联合夏风教室发起“劳动最光荣,加油好少年”主题活动.某校学生积极参与本次主题活动,为了解该校学生参与本次主题活动的情况,随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图(如图).请结合图中信息解答下列问题:
(1)本次共调查了 名学生,并补全条形统计图;
(2)若该校共有1 200名学生参加本次主题活动,则本次活动中该校“洗衣服”的学生约有多少名
(3)现从参与本次主题活动的甲、乙、丙、丁4名学生中,随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法,求甲、乙两人同时被抽中的概率.
21.(8分)我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”(如图①).数学兴趣小组利用无人机测量古槐的高度,如图②所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米E点处时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B与树底D的水平距离为20米,求古槐的高度(结果精确到1米).
(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50,sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
22.(8分)如图,在矩形ABCD中,E是AB上一点,连接CE,以CE为直径的☉O与AD边交于点F,交CD于点G,连接OF,GF,EF,若∠BEC=∠CEF=60°,AF=2.
(1)试判断☉O与AD的位置关系,并说明理由;
(2)求矩形ABCD的周长;
(3)求阴影部分的面积.
23.(10分)为全面贯彻党的教育方针,严格落实教育部对中小学生“五项管理”的相关要求和《关于进一步加强中小学生体质健康管理工作的通知》精神,保障学生每天在校1小时体育活动时间,某班计划采购A,B两种类型的羽毛球拍.已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
(1)求A,B两种类型羽毛球拍的单价;
(2)该班准备采购A,B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.
24.(10分)如图,在平面直角坐标系中,四边形AOBC是矩形,OB=4,OA=3,F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=(k>0)的图象与边AC交于点E.
(1)当BF=BC时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)将△EFC沿EF折叠,得到△EFG,当点G恰好落在矩形AOBC的对角线上时,求k的值.
25.(12分)如图,在Rt△ABC中,∠ABC=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题1 当α=0°时,AE/BD=_____.
问题2 当α=180°时,AE/BD=_____.
问题3 试判断:当0°≤α<360°时,的大小有无变化 请根据如图的情形给出证明.
问题4 当△EDC旋转至A,D,E三点共线时,求线段BD的长.
26.(12分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形 若存在,请直接写出所有P点的坐标,若不存在,请说明理由.
山东省济南市莱芜区2023年初中学业水平考试模拟冲刺卷(二)
(120分钟 150分)
第Ⅰ卷(选择题,共40分)
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B D C B D C A C
第Ⅱ卷(非选择题,共110分)
二、填空题(本大题共6个小题,每小题4分,满分24分.直接填写最后结果)
11. x(x-3)(x+1) 12. 9 13. 14. 1 260° 15. ①②③ 16. (-5,-4)或(0,1)
三、解答题(本大题共10小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
17.(6分)计算:(-1)2 021+|-2|+4sin 30°-(√(3&8)-π)0.
【解析】原式=-1+2+4×-1=-1+2+2-1=2.
18.(6分)解不等式组,并将解集表示在所给的数轴上.
【解析】,
解①得:x>2,解②得:x≤4,
故不等式组的解集是:2
19.(6分)如图,已知平行四边形ABCD中,F,G是AB边上的两个点,且FC平分∠BCD,GD平分∠ADC,FC与GD相交于点E,求证:AF=GB.
【证明】在平行四边形ABCD中,∵DG,CF分别平分∠ADC,∠BCD,
∴∠ADG=∠CDG,∠DCF=∠BCF,
又∵∠CDG=∠AGD,∠DCF=∠BFC,
∴∠ADG=∠AGD,∠BCF=∠BFC,
∴AG=AD,BF=BC,又∵AD=BC,∴AG=BF,
∴AF=GB.
20.(8分)2022年4月29日,湖北日报联合夏风教室发起“劳动最光荣,加油好少年”主题活动.某校学生积极参与本次主题活动,为了解该校学生参与本次主题活动的情况,随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图(如图).请结合图中信息解答下列问题:
(1)本次共调查了 名学生,并补全条形统计图;
(2)若该校共有1 200名学生参加本次主题活动,则本次活动中该校“洗衣服”的学生约有多少名
(3)现从参与本次主题活动的甲、乙、丙、丁4名学生中,随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法,求甲、乙两人同时被抽中的概率.
【解析】(1)40÷20%=200(人),
200-40-50-30-20=60(人),补全条形统计图如图:
答案:200
(2)1 200×=300(人),
答:该校1 200名学生中参与“洗衣服”的学生约有300名;
(3)从甲、乙、丙、丁四个人中选择2个人所有等可能出现的结果情况如表:
第2人 第1人
甲 乙 丙 丁
甲 - 乙甲 丙甲 丁甲
乙 甲乙 - 丙乙 丁乙
丙 甲丙 乙丙 - 丁丙
丁 甲丁 乙丁 丙丁 -
共有12种等可能出现的结果,其中甲、乙同时被抽中的情况有2种,
所以甲、乙同时被抽中的概率为=.
21.(8分)我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”(如图①).数学兴趣小组利用无人机测量古槐的高度,如图②所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米E点处时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B与树底D的水平距离为20米,求古槐的高度(结果精确到1米).
(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50,sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
【解析】过点A作AM⊥EH于M,过点C作CN⊥EH于N,
由题意知,AM=BH,CN=DH,AB=MH,
在Rt△AME中,∠EAM=26.6°,
∴tan∠EAM=EM/AM,
∴AM=EM/tan∠EAM=EH MH/tan26.6°≈45 39/0.5=12(米),∴BH=AM=12米,
∵BD=20,∴DH=BD-BH=8(米),∴CN=8米,
在Rt△ENC中,∠ECN=76°,∴tan∠ECN=EN/CN,
∴EN=CN·tan∠ECN≈8×4.01=32.08(米),
∴CD=NH=EH-EN=12.92≈13(米),
答:古槐的高度约为13米.
22.(8分)如图,在矩形ABCD中,E是AB上一点,连接CE,以CE为直径的☉O与AD边交于点F,交CD于点G,连接OF,GF,EF,若∠BEC=∠CEF=60°,AF=2.
(1)试判断☉O与AD的位置关系,并说明理由;
(2)求矩形ABCD的周长;
(3)求阴影部分的面积.
【解析】(1)☉O与AD相切,
理由:∵四边形ABCD是矩形,∴∠A=90°,
∵∠BEC=∠CEF=60°,
∴∠AEF=180°-∠BEC-∠OEF=60°,∵OF=OE,
∴△OEF是等边三角形,∴∠OFE=60°,∴∠OFE=∠AEF,
∵OF∥AB,∴∠OFA+∠A=180°,∴∠OFA=90°,
∵OF是☉O的半径,∴☉O与AD边相切;
(2)∵四边形ABCD是矩形,∴∠A=∠D=90°,
∴CD⊥AD,BA⊥AD,∴CD∥OF∥AB,∴==1,
∴DF=AF=2,∴AD=4=BC,
∵∠CEB=60°,∠B=90°,∴∠BCE=30°,∴CE=2BE,
∵BC2+BE2=CE2,∴(4)2+BE2=(2BE)2,
∴BE=4,CE=8,
∴OF=OC=OE=4,∠AEF=60°,∠A=90°,AF=2,∴AE=2,
∴CD=AB=6,∴C矩形ABCD=2×(6+4)=12+8;
(3)如图,连接OG,∵CD∥OF∥AB,
∴∠OCG=∠BEC=60°,S△CFG=S△COG,∵OC=OG,
∴△OCG是等边三角形,∴∠COG=60°,
∴S阴影==π.
23.(10分)为全面贯彻党的教育方针,严格落实教育部对中小学生“五项管理”的相关要求和《关于进一步加强中小学生体质健康管理工作的通知》精神,保障学生每天在校1小时体育活动时间,某班计划采购A,B两种类型的羽毛球拍.已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
(1)求A,B两种类型羽毛球拍的单价;
(2)该班准备采购A,B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.
【解析】(1)设A种羽毛球拍每副x元,B种羽毛球拍每副y元,
,解得,
答:A种羽毛球拍每副40元,B种羽毛球拍每副32元.
(2)设购买B种羽毛球拍a副,总费用w元,
依题意得30-a≥2a,解得a≤10,
w=40(30-a)+32a=-8a+1 200,
∵-8<0,∴w随a的增大而减小,
∴当a=10时,w最小,w最小=-8×10+1 200=1 120(元),
此时30-10=20(副),
答:费用最少的方案是购买A种羽毛球拍20副,B种羽毛球拍10副,所需费用1 120元.
24.(10分)如图,在平面直角坐标系中,四边形AOBC是矩形,OB=4,OA=3,F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=(k>0)的图象与边AC交于点E.
(1)当BF=BC时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)将△EFC沿EF折叠,得到△EFG,当点G恰好落在矩形AOBC的对角线上时,求k的值.
【解析】(1)∵OB=4,OA=3,∴点A,B的坐标分别为(0,3),(4,0).∵四边形OACB为矩形,则点C(4,3),
当BF=BC时,点F(4,1),将点F的坐标代入y=,解得:k=4,故反比例函数的表达式为:y=,
当y=3时,x=,故E,3;
(2)∵F点的横坐标为4,点F在反比例函数上,
∴F4,,∴CF=BC-BF=3-=,
∵E的纵坐标为3,∴E,3,
∴CE=AC-AE=4-k=,
在Rt△CEF中,tan ∠EFC==;
(3)①当点G落在对角线AB上时,在Rt△ABC中,tan ∠ABC===tan ∠EFC,
故EF∥AB,
连接CG交EF于点M,则MG=MC,
即点M是CG的中点,而EF∥AB,
故MF是△CGB的中位线,则点F是BC的中点,
故点F的坐标为4,,将点F的坐标代入反比例函数表达式得:k=4×=6;
②当点G落在OC上时,由①知,CG⊥AB,如果G落在OC上,则OC⊥AB,由题意得AB和OC不垂直,
故点G不会落在OC上.综上,k=6.
25.(12分)如图,在Rt△ABC中,∠ABC=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题1 当α=0°时,AE/BD=_____.
问题2 当α=180°时,AE/BD=_____.
问题3 试判断:当0°≤α<360°时,的大小有无变化 请根据如图的情形给出证明.
【解析】当0°≤α<360°时,的大小没有变化.
∵∠ECD=∠ACB,∴∠ECA=∠DCB,
又∵==,∴△ECA∽△DCB,
∴==.
问题4 当△EDC旋转至A,D,E三点共线时,求线段BD的长.
【解析】如图①,当△EDC绕点C顺时针旋转90°时,直线DE经过点A,连接BD.
∵AC=,CD=6,CD⊥AD,
∴AD===12,
∵AD=BC,AB=DC,∴四边形ABCD是平行四边形,
∵∠ABC=90°,∴四边形ABCD是矩形,
∴BD=AC=.
如图②,当△EDC绕点C顺时针旋转至此位置时,直线DE经过点A.连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
∵AC=,CD=6,CD⊥AD,
∴AD==12,
∴AE=AD-DE=12-3=9,
由问题3可得,=,
∴BD==.
综上所述,BD的长为或.
26.(12分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形 若存在,请直接写出所有P点的坐标,若不存在,请说明理由.
【解析】(1)∵二次函数y=ax2+bx+c经过点A(-4,0),B(2,0),C(0,6),
∴解得
所以二次函数的表达式为y=-x2-x+6;
(2)由A(-4,0),E(0,-2),可求AE所在直线表达式为y=-x-2,
过点D作DG⊥x轴于G,交AE于点F,过点E作EH⊥DF,垂足为H,如图.
设Dm,-m2-m+6,则点Fm,-m-2,
∴DF=-m2-m+6--m-2
=-m2-m+8,
∴S△ADE=S△ADF+S△EDF=×DF×AG+DF×EH
=×DF×(AG+EH)=×4×DF
=2×-m2-m+8=-m+2+,
∴当m=-时,△ADE的面积取得最大值为;
(3)y=-x2-x+6的对称轴为x=-1,
设P(-1,n),又E(0,-2),A(-4,0),
可求PA2=9+n2,PE2=1+(n+2)2,AE2=16+4=20,
当PA2=PE2时,9+n2=1+(n+2)2,
解得,n=1,此时P(-1,1);
当PA2=AE2时,9+n2=20,
解得,n=±,此时点P坐标为(-1,±);
当PE2=AE2时,1+(n+2)2=20,
解得,n=-2±,此时点P坐标为:(-1,-2±).
综上所述,P点的坐标为:(-1,1),(-1,±),(-1,-2±).
同课章节目录
