北京课改版初中数学九年级上册 第十九章 二次函数的图像与性质 复习教案(表格式,含练习)
文档属性
| 名称 | 北京课改版初中数学九年级上册 第十九章 二次函数的图像与性质 复习教案(表格式,含练习) |

|
|
| 格式 | docx | ||
| 文件大小 | 95.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 10:23:15 | ||
图片预览


文档简介
二次函数的图象与性质 复习课
一、教学目标
1.复习二次函数图象与性质的基础知识(解析式、顶点坐标、对称轴、增减性).
2. 让学生经历读图过程,学会多维度的识图读图,学习一般的提取图象信息的方法. 学会对获得的信息进行归类,并纳入知识体系.
3. 感受数形结合、转化思想在问题中的运用.
二、学情及重难点分析
本班学生数学基础较好,课堂活跃. 已基本掌握二次函数图象与性质的基础知识(解析式、顶点坐标、对称轴、增减性),从前测数据分析,学生对于二次函数的图象表面信息的获取,以及单一图象的读图和解析式的求法,问题都不大;本节课试图引导学生通过“形(图象特征)----数(数式表达 )”的转换过程,充分理解具体问题中数形结合的“结合点”(解析式、顶点坐标、对称轴、增减性).
重难点在二次函数图象与性质的多维度解读,并纳入知识体系.
三、前测(提前一天做线下练习,学生统一时间做,收集数据,对学生出错率高的问题重点讲解)
说明:前测题目共8题,考查内容包括:二次函数的定义,二次函数解析式,系数a,b,c在图象中的体现,抛物线的图象特征与表达(与两个坐标轴的交点,顶点,对称轴,增减性),图表信息的提取与转换,抛物线与一次函数的结合.
考查的数学思想方法包括:数形结合,转化思想,方程思想.
四、课堂教学过程:
环节1.前测问题反馈----对的错的都弄通
对得分率不理想的题目讲清楚(小组学习----集体汇报.特别体现学生的自主学习与合作交流,鼓励学生讲出来).老师归纳提升,重点内容板书.
解析式:(一般式、顶点式、交点式)
抛物线位置由a、b、c决定(各自管什么,怎么管)
环节2.开放性问题---基本图形我来读
二次函数的部分图象如图所示,当x取一切实数时,请将图象补充完整,写出3个以上的正确结论,并说明理由.
这是一个开放性问题。可以写出一系列的式子。给学生足够的时间,写出结论,并交流.
(1)看整体
图象特征(形) 数式表达(数) 数形结合的结合点
抛物线() 系数a,b,c待定 二次函数的图象是一条抛物线.
函数图象是抛物线,且开口向下 决定图象开口方向 a>0开口向上;a<0开口向下
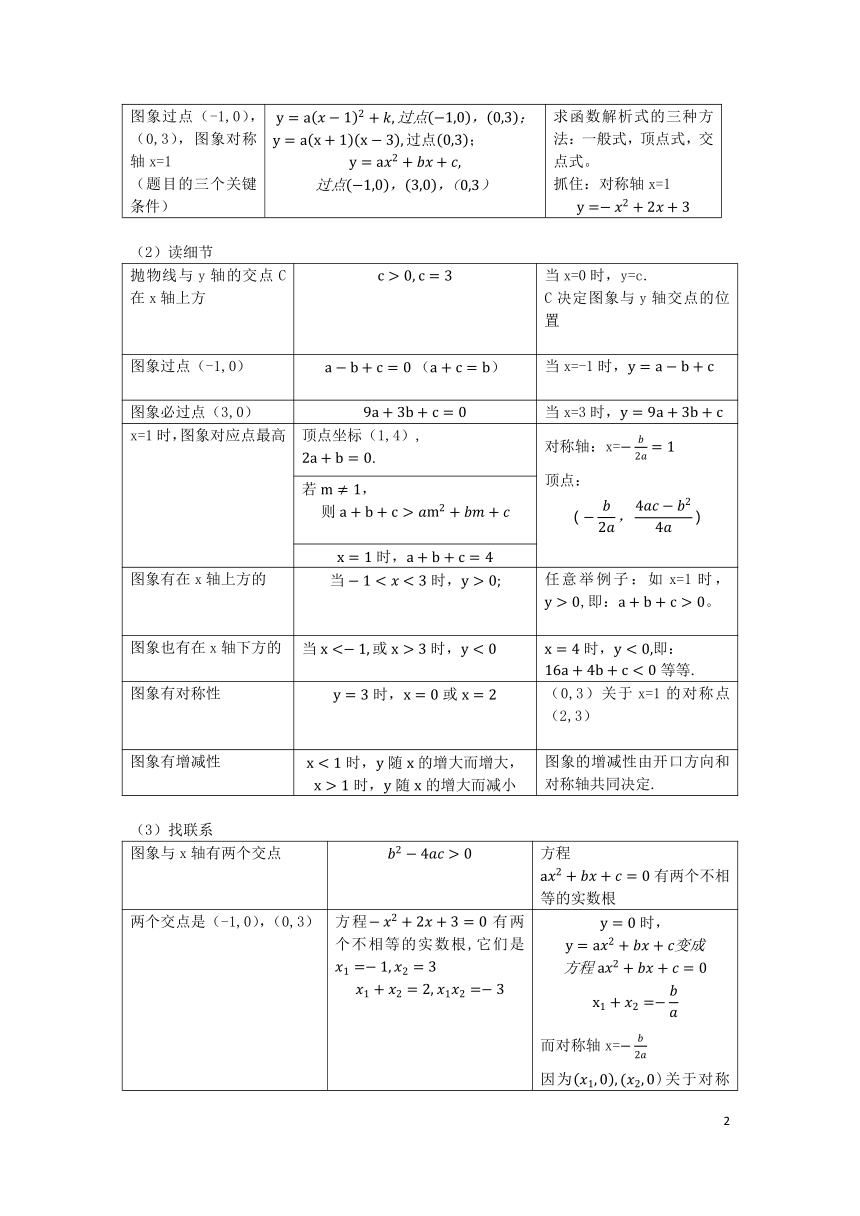
图象过点(-1,0),(0,3),图象对称轴x=1 (题目的三个关键条件) ; 求函数解析式的三种方法:一般式,顶点式,交点式。 抓住:对称轴x=1
(2)读细节
抛物线与y轴的交点C在x轴上方 当x=0时,y=c. C决定图象与y轴交点的位置
图象过点(-1,0) 当x=-1时,
图象必过点(3,0) 当x=3时,
x=1时,图象对应点最高 顶点坐标(1,4), . 对称轴:x= 顶点:
若
图象有在x轴上方的 任意举例子:如x=1时,,即:。
图象也有在x轴下方的 当 即: 等等.
图象有对称性 (0,3)关于x=1的对称点(2,3)
图象有增减性 图象的增减性由开口方向和对称轴共同决定.
(3)找联系
图象与x轴有两个交点 方程
a有两个不相等的实数根
两个交点是(-1,0),(0,3) 方程有两个不相等的实数根,它们是 而对称轴x= 因为)关于对称轴对称, 所以
对称轴x=
顶点纵坐标 方程有唯一解x=1 方程无解 当m取何值,方程有解.
设计意图:通过相关结论的挖掘,旨在帮助学生对二次函数核心知识进行重点回顾。内容上试图将二次函数,一元二次方程、不等式、轴对称等相关知识以适当的载体进行融合,以达到知识间的融会贯通,提升复习实效.
学生活动:每个同学尽可能的写出自己的结论,小组交流,集体汇总,及点出相应的知识点,并对该知识点进行描述.
环节3.问题回想---数学味道我来品
1.方法解读---如何识图(脚手架)
如何识图 心中有个脚手架
1.这是一个什么函数的图象 二次函数(自变量的取值范围,函数值的范围,对应关系)
2.二次函数解析式 三种解析式表达方法,选哪一种?
3.图象特征 开口(方向,大小)?对称轴? 顶点坐标?-----该记的要记清楚.
4.关键点 与坐标轴的交点.图象中出现的所有点
5.增减性 图象的变化趋势----对称轴起着关键作用
2.欣赏你的结论----由小见大,建构我的数学王国
形(一个小小的图象)----数(一串长长的结论).
表面的----深层的(多看多想).
环节4. 问题延伸----题目我来编
在写结论过程中,你认为哪个条件最重要,想不想改变一下?编个题目来试试.
老师的思考:1.对称轴变为x=n,其他条件不变,我们来研究研究.
举个例子:从形上解释----由图象的对称性:
从数上解释----用数式的方式,你怎么做?
过点(-1,0),(0,3)
解出,可得 是不是跟用图象做的判断一致呢?
从a的表达式,你得到什么?何时开口向上?向下?
2.若对称轴,其他条件不变,你能分析的取值范围吗?
同学们继续研究,做为我们本周的探索性训练问题,加油!
设计意图:编题过程是课堂学习的延续,题目3个关键条件只要有一个变动,问题就动起来了,这是我们所做的探索性训练的问题源泉.(探索性训练的模式,是我们备组三年来坚持的做法,每周根据所学知识,都有2-4道的探索性问题,学生通过自己学习,同伴交流,课堂分析,到课后做到数学笔记一系列的过程,体会数学思考、同伴交流的乐趣.)
附件1:前测
一、选择题(共5小题 , 共61分)
1. 函数y=(m-n)x2+mx+n是二次函数的条件是( )
A.m、n是常数,且 m≠0 B. m、n是常数,且m≠ n
C.m、n是常数,且n≠0 D.m、n可以为任何常数
2. 已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
A. B. C. D.
3. 在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
A. B. C. D.
4. 小军从所给的二次函数图象中观察得出了下面的信息:①a<0;②c=0;③函数的最小值是-3;④当x<0时y>0;⑤当0<x1<x2<2时y1>y2.你认为其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
5. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … -2 -1 0 1 2 …
y … -11 -2 1 -2 -5 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.-11 B.-2 C.1 D.-5
二、填空题 (共3小题 , 共39分)
6. 已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是_____.
7. 二次函数y=x2+x-6的图象与y轴的交点坐标是_____,与x轴交点的坐标是_____.
8. 如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是_____.
附件:后测
一、选择题(共6小题 , 共100分)
1. 对于二次函数y=+x-4, 下列说法正确的是( )
A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7) D.图象与x轴有两个交点
2. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.-3 B.3 C.-6 D.9
3. 如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
4. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2-b的图象可能是( )
A. B. C. D.
5. 已知二次函数y=-x2+bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-2 B.b≤-2 C.b≥2 D.b≤2
2
一、教学目标
1.复习二次函数图象与性质的基础知识(解析式、顶点坐标、对称轴、增减性).
2. 让学生经历读图过程,学会多维度的识图读图,学习一般的提取图象信息的方法. 学会对获得的信息进行归类,并纳入知识体系.
3. 感受数形结合、转化思想在问题中的运用.
二、学情及重难点分析
本班学生数学基础较好,课堂活跃. 已基本掌握二次函数图象与性质的基础知识(解析式、顶点坐标、对称轴、增减性),从前测数据分析,学生对于二次函数的图象表面信息的获取,以及单一图象的读图和解析式的求法,问题都不大;本节课试图引导学生通过“形(图象特征)----数(数式表达 )”的转换过程,充分理解具体问题中数形结合的“结合点”(解析式、顶点坐标、对称轴、增减性).
重难点在二次函数图象与性质的多维度解读,并纳入知识体系.
三、前测(提前一天做线下练习,学生统一时间做,收集数据,对学生出错率高的问题重点讲解)
说明:前测题目共8题,考查内容包括:二次函数的定义,二次函数解析式,系数a,b,c在图象中的体现,抛物线的图象特征与表达(与两个坐标轴的交点,顶点,对称轴,增减性),图表信息的提取与转换,抛物线与一次函数的结合.
考查的数学思想方法包括:数形结合,转化思想,方程思想.
四、课堂教学过程:
环节1.前测问题反馈----对的错的都弄通
对得分率不理想的题目讲清楚(小组学习----集体汇报.特别体现学生的自主学习与合作交流,鼓励学生讲出来).老师归纳提升,重点内容板书.
解析式:(一般式、顶点式、交点式)
抛物线位置由a、b、c决定(各自管什么,怎么管)
环节2.开放性问题---基本图形我来读
二次函数的部分图象如图所示,当x取一切实数时,请将图象补充完整,写出3个以上的正确结论,并说明理由.
这是一个开放性问题。可以写出一系列的式子。给学生足够的时间,写出结论,并交流.
(1)看整体
图象特征(形) 数式表达(数) 数形结合的结合点
抛物线() 系数a,b,c待定 二次函数的图象是一条抛物线.
函数图象是抛物线,且开口向下 决定图象开口方向 a>0开口向上;a<0开口向下
图象过点(-1,0),(0,3),图象对称轴x=1 (题目的三个关键条件) ; 求函数解析式的三种方法:一般式,顶点式,交点式。 抓住:对称轴x=1
(2)读细节
抛物线与y轴的交点C在x轴上方 当x=0时,y=c. C决定图象与y轴交点的位置
图象过点(-1,0) 当x=-1时,
图象必过点(3,0) 当x=3时,
x=1时,图象对应点最高 顶点坐标(1,4), . 对称轴:x= 顶点:
若
图象有在x轴上方的 任意举例子:如x=1时,,即:。
图象也有在x轴下方的 当 即: 等等.
图象有对称性 (0,3)关于x=1的对称点(2,3)
图象有增减性 图象的增减性由开口方向和对称轴共同决定.
(3)找联系
图象与x轴有两个交点 方程
a有两个不相等的实数根
两个交点是(-1,0),(0,3) 方程有两个不相等的实数根,它们是 而对称轴x= 因为)关于对称轴对称, 所以
对称轴x=
顶点纵坐标 方程有唯一解x=1 方程无解 当m取何值,方程有解.
设计意图:通过相关结论的挖掘,旨在帮助学生对二次函数核心知识进行重点回顾。内容上试图将二次函数,一元二次方程、不等式、轴对称等相关知识以适当的载体进行融合,以达到知识间的融会贯通,提升复习实效.
学生活动:每个同学尽可能的写出自己的结论,小组交流,集体汇总,及点出相应的知识点,并对该知识点进行描述.
环节3.问题回想---数学味道我来品
1.方法解读---如何识图(脚手架)
如何识图 心中有个脚手架
1.这是一个什么函数的图象 二次函数(自变量的取值范围,函数值的范围,对应关系)
2.二次函数解析式 三种解析式表达方法,选哪一种?
3.图象特征 开口(方向,大小)?对称轴? 顶点坐标?-----该记的要记清楚.
4.关键点 与坐标轴的交点.图象中出现的所有点
5.增减性 图象的变化趋势----对称轴起着关键作用
2.欣赏你的结论----由小见大,建构我的数学王国
形(一个小小的图象)----数(一串长长的结论).
表面的----深层的(多看多想).
环节4. 问题延伸----题目我来编
在写结论过程中,你认为哪个条件最重要,想不想改变一下?编个题目来试试.
老师的思考:1.对称轴变为x=n,其他条件不变,我们来研究研究.
举个例子:从形上解释----由图象的对称性:
从数上解释----用数式的方式,你怎么做?
过点(-1,0),(0,3)
解出,可得 是不是跟用图象做的判断一致呢?
从a的表达式,你得到什么?何时开口向上?向下?
2.若对称轴,其他条件不变,你能分析的取值范围吗?
同学们继续研究,做为我们本周的探索性训练问题,加油!
设计意图:编题过程是课堂学习的延续,题目3个关键条件只要有一个变动,问题就动起来了,这是我们所做的探索性训练的问题源泉.(探索性训练的模式,是我们备组三年来坚持的做法,每周根据所学知识,都有2-4道的探索性问题,学生通过自己学习,同伴交流,课堂分析,到课后做到数学笔记一系列的过程,体会数学思考、同伴交流的乐趣.)
附件1:前测
一、选择题(共5小题 , 共61分)
1. 函数y=(m-n)x2+mx+n是二次函数的条件是( )
A.m、n是常数,且 m≠0 B. m、n是常数,且m≠ n
C.m、n是常数,且n≠0 D.m、n可以为任何常数
2. 已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
A. B. C. D.
3. 在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
A. B. C. D.
4. 小军从所给的二次函数图象中观察得出了下面的信息:①a<0;②c=0;③函数的最小值是-3;④当x<0时y>0;⑤当0<x1<x2<2时y1>y2.你认为其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
5. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … -2 -1 0 1 2 …
y … -11 -2 1 -2 -5 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.-11 B.-2 C.1 D.-5
二、填空题 (共3小题 , 共39分)
6. 已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是_____.
7. 二次函数y=x2+x-6的图象与y轴的交点坐标是_____,与x轴交点的坐标是_____.
8. 如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是_____.
附件:后测
一、选择题(共6小题 , 共100分)
1. 对于二次函数y=+x-4, 下列说法正确的是( )
A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7) D.图象与x轴有两个交点
2. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.-3 B.3 C.-6 D.9
3. 如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
4. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2-b的图象可能是( )
A. B. C. D.
5. 已知二次函数y=-x2+bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-2 B.b≤-2 C.b≥2 D.b≤2
2
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
