第七章随机变量及其分布“四步复习法”单元复习讲义(有答案)
文档属性
| 名称 | 第七章随机变量及其分布“四步复习法”单元复习讲义(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 20:39:42 | ||
图片预览




文档简介
第七章 随机变量及其分布
——2022-2023学年高二数学人教A版(2019)选择性必修第三册
大单元“四步复习法”
第一步:单元学习目标整合
1.条件概率与全概率公式 (1)了解条件概率,能计算简单随机事件的条件概率. (2)了解条件概率与独立性的关系,会利用乘法公式计算概率. (3)会利用全概率公式计算概率.
2.离散型随机变量及其分布列 (1)理解离散型随机变量的含义,会用离散型随机变量描述随机现象. (2)掌握离散型随机变量分布列的表示方法及性质,了解两点分布.
3.离散型随机变量的数字特征 (1)理解离散型随机变量的均值、方差的概念,能计算简单离散型随机变量的均值、方差. (2)理解离散型随机变量的均值、方差的性质. (3)会利用离散型随机变量的均值、方差解决简单的实际问题.
4.二项分布与超几何分布 (1)掌握二项分布及其数字特征,并能解决简单的实际问题. (2)了解超几何分布及其均值,并能解决简单的实际问题.
5.正态分布 (1)了解服从正态分布的随机变量,了解正态分布的特征. (2)了解正态分布的均值、方差及其含义.
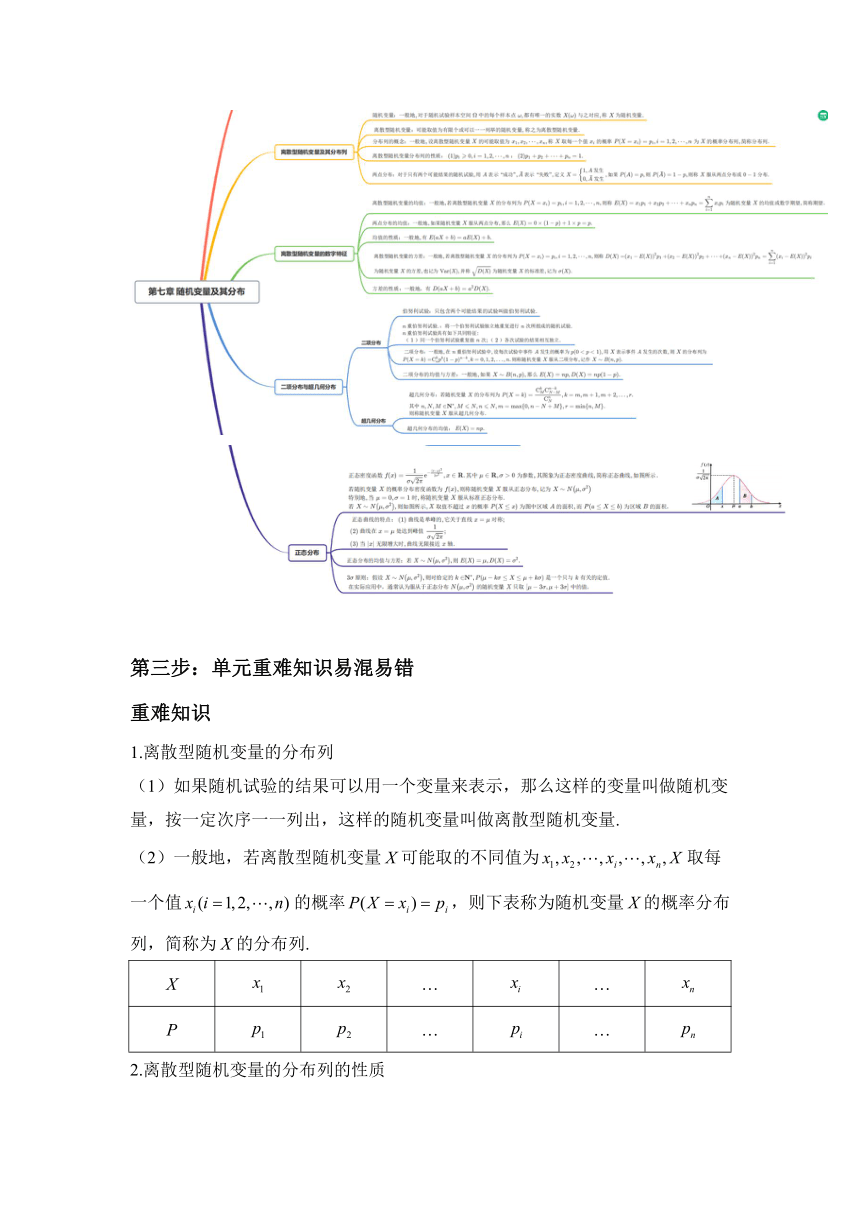
第二步:单元思维导图回顾知识
第三步:单元重难知识易混易错
重难知识
1.离散型随机变量的分布列
(1)如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量,按一定次序一一列出,这样的随机变量叫做离散型随机变量.
(2)一般地,若离散型随机变量X可能取的不同值为取每一个值的概率,则下表称为随机变量X的概率分布列,简称为X的分布列.
X … …
P … …
2.离散型随机变量的分布列的性质
根据概率的性质,离散型随机变量的分布列具有如下性质:
(1);
(2);
(3).
3.常见的离散型随机变量的概率分布模型
(1)两点分布
若随机变量X的分布列为
X 0 1
P p
则称X服从两点分布.
(2)超几何分布
一般地,在含有M件次品的N件产品中任取n件,其中恰有X件次品,则
,其中,且,称分布列
X 0 1 … m
P …
为超几何分布.
4.离散型随机变量的均值与方差
若离散型随机变量X的分布列为
X … …
P … …
(1)均值:称为随机变量X的均值或数学期望,它反映了离散型随机变量取值的平均水平.
(2)方差:称为随机变量X的方差,它刻画了随机变量X与其均值的平均偏离程度,并称为随机变量X的标准差,记为.
5.均值与方差的性质
(1).
(2).
6.两点分布的均值、方差
若X服从两点分布,则.
7.条件概率及其性质
(1)一般地,设A,B为两个事件,且,称为在事件A发生的条件下,事件B发生的概率.
(2)条件概率的性质:
(i);
(ii)如果B和C是两个互斥事件,则.
8.全概率公式
一般地,设是一组两两互斥的事件,,且,则对任意的事件,有,称此公式为全概率公式.
9.二项分布的均值与方差:若,则,.
10.正态曲线的定义:
函数(其中实数和为参数)的图象为正态分布密度曲线,简称正态曲线.
11.正态分布的定义及表示:
如果对于任何实数,随机变量X满足,则称X的分布为正态分布,记作.
典型例题
1.环境空气质量监测资料表明,某地一天的空气质量为轻度污染的概率是0.25,连续两天为轻度污染的概率是0.1,则此地在某天的空气质量为轻度污染的条件下,随后一天的空气质量也为轻度污染的概率是( )
A.0.4 B.0.25 C.0.1 D.0.05
2.通讯中常采取重复发送信号的办法来减少在接收中可能发生的错误,假定接收一个信号时发生错误的概率是,为减少错误,采取每一个信号连发3次,接收时以“少数服从多数”的原则判断,则判错一个信号的概率为( )
A. B. C. D.
3.若随机变量X的分布列为
X 0 1
P 0.2 m
已知随机变量,且,则a与b的值为( )
A. B. C. D.
4.一批产品分为一,二,三3个等级,其中一级品的个数是二级品的两倍,三级品的个数是二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量,则__________.
5.已知服从正态分布的随机变量在区间内取值的概率分别为0.683,0.954,0.997.若某种袋装大米的质量X(单位:)服从正态分布,任意选一袋这种大米,质量在的概率为_________________.
6.为进一步激发青少年学习中华优秀传统文化的热情,某校举办了“我爱古诗词”对抗赛,在每轮对抗赛中,高二年级胜高三年级的概率为,高一年级胜高三年级的概率为,且每轮对抗赛的成绩互不影响.
(1)若高二年级与高三年级进行4轮对抗赛,求高三年级在对抗赛中至少有3轮胜出的概率;
(2)若高一年级与高三年级进行对抗,高一年级胜2轮就停止,否则开始新一轮对抗,但对抗不超过5轮,求对抗赛轮数X的分布列与数学期望.
答案以及解析
1.答案:A
解析:设事件A:一天的空气质量为轻度污染,事件B:随后一天的空气质量也为轻度污染,由题知,所以.故选A.
2.答案:B
解析:得到正确信号的概率有两种情形,一种情形是三次接收正确,概率为,另一种情形是两次接收正确,一次接收不正确,概率为,所以判错一个信号的概率为,故选B.
3.答案:C
解析:由随机变量X的分布列可知,,
,,
,,
,,,故选C.
4.答案:
解析:设二级品有k个,则一级品有个,三级品有个,总数为个,则级别的分布列为
1 2 3
P
.
5.答案:0.818 5
解析:根据题意得到质量在到之间的大米概率为0.954,则小于的大米的概率为;质量在到之间的大米的概率为0.683,故质量大于的大米的概率为.故质量在的大米的概率为.
6.答案:(1)
(2)分布列见解析,
解析:(1)由题意知,高三年级胜高二年级的概率为.
设高三年级在4轮对抗赛中有x轮胜出,“至少有3轮胜出”的概率为P,
则.
(2)由题意知,对抗赛轮数X的所有可能取值为2,3,4,5,
则,
,
,
,
故X的分布列为
X 2 3 4 5
P
.
第四步:单元核心素养对接高考
核心素养
离散型随机变量及其分布列、均值与方差是高考的热点,常以实际问题为背景,与计数原理、古典概型等知识相结合,考查离散型随机变量的分布列、均值和方差,要特别注意二项分布与超几何分布问题及利用期望与方差决策的问题,主要以解答题的形式呈现,难度中等,近两年难度有加大的趋势,更加重视对考生的实际应用能力的考查,要重视对实际问题背景的分析与了解,要在审题、转化、建模等问题上下功夫,重视与其他知识的综合应用.
二项分布及其应用、正态分布是高考的热点,主要考查:①条件概率、相互独立事件的概率的求法,一般以选择题、填空题的形式出现,有时也会渗透在解答题中;②独立重复试验、二项分布、正态分布的应用,结合实际问题以解答题的形式出现.解题时注意对相关概念的理解及相关公式的应用.主要考查考生的数据分析能力.
真题对接
1.【2021年 新高考ⅠⅠ卷,6】某物理量的测量结果服从正态分布,则下列结论中不正确的是( )
A.σ越小,该物理量一次测量结果落在内的概率越大
B.σ越小,该物理量一次测量结果大于10的概率为0.5
C.σ越小,该物理量一次测量结果大于10.01与小于9.99的概率相等
D.σ越小,该物理量一次测量结果落在内的概率与落在内的概率相等
2.【2022年 新高考ⅠⅠ卷,19】在某地区进行流行病调查,随机调查了100名某种疾病患者的年龄,得到如下的样本数据频率分布直方图.
(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值作代表);
(2)估计该地区一位这种疾病患者的年龄位于区间的概率;
(3)已知该地区这种疾病的患病率为0.1%,该地区年龄位于区间的人口占该地区总人口的16%,从该地区中任选一人,若此人的年龄位于区间,求此人患这种疾病的概率(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001).
3.【2021年 新高考Ⅰ卷,18】某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题 并说明理由.
答案以及解析
1.答案:D
解析:本题考查正态曲线的特点.根据正态曲线可直接得出B项, C项正确;越小,则正态曲线越“瘦高”,该物理量一次测量结果落在内的概率越大,A项正确;同理,落在内的概率大于落在内的概率,D项错误.
2.解析:(1)估计该地区这种疾病患者的平均年龄.
(2)解法一由于患者的年龄位于区间是由患者的年龄位于区间,,,,组成的,且相互独立,
所以所求概率.
解法二由于患者的年龄位于区间是由患者的年龄位于区间,,,,组成的,且相互独立,
所以所求概率.
(3)设从该地区任选一人,年龄位于区间为事件A,患这种疾病为事件B,
则,
由频率分布直方图知这种疾病患者年龄位于区间的概率为,
结合该地区这种疾病的患病率为0.1%,可得,
所以从该地区任选一人,若年龄位于区间,
则此人患这种疾病的概率为.
3.解析:(1)X的所有可能取值为0,20,100.
,
,
,
所以X的分布列为
X 0 20 100
P 0.2 0.32 0.48
(2)假设先答B类问题,记Y为小明的累计得分,
则Y的所有可能取值为0,80,100.
,
,
,
所以Y的分布列为
Y 0 80 100
P 0.4 0.12 0.48
所以,
由(1)可知.
因为,
所以为使累计得分的期望最大,小明应选择先回答B类问题.
——2022-2023学年高二数学人教A版(2019)选择性必修第三册
大单元“四步复习法”
第一步:单元学习目标整合
1.条件概率与全概率公式 (1)了解条件概率,能计算简单随机事件的条件概率. (2)了解条件概率与独立性的关系,会利用乘法公式计算概率. (3)会利用全概率公式计算概率.
2.离散型随机变量及其分布列 (1)理解离散型随机变量的含义,会用离散型随机变量描述随机现象. (2)掌握离散型随机变量分布列的表示方法及性质,了解两点分布.
3.离散型随机变量的数字特征 (1)理解离散型随机变量的均值、方差的概念,能计算简单离散型随机变量的均值、方差. (2)理解离散型随机变量的均值、方差的性质. (3)会利用离散型随机变量的均值、方差解决简单的实际问题.
4.二项分布与超几何分布 (1)掌握二项分布及其数字特征,并能解决简单的实际问题. (2)了解超几何分布及其均值,并能解决简单的实际问题.
5.正态分布 (1)了解服从正态分布的随机变量,了解正态分布的特征. (2)了解正态分布的均值、方差及其含义.
第二步:单元思维导图回顾知识
第三步:单元重难知识易混易错
重难知识
1.离散型随机变量的分布列
(1)如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量,按一定次序一一列出,这样的随机变量叫做离散型随机变量.
(2)一般地,若离散型随机变量X可能取的不同值为取每一个值的概率,则下表称为随机变量X的概率分布列,简称为X的分布列.
X … …
P … …
2.离散型随机变量的分布列的性质
根据概率的性质,离散型随机变量的分布列具有如下性质:
(1);
(2);
(3).
3.常见的离散型随机变量的概率分布模型
(1)两点分布
若随机变量X的分布列为
X 0 1
P p
则称X服从两点分布.
(2)超几何分布
一般地,在含有M件次品的N件产品中任取n件,其中恰有X件次品,则
,其中,且,称分布列
X 0 1 … m
P …
为超几何分布.
4.离散型随机变量的均值与方差
若离散型随机变量X的分布列为
X … …
P … …
(1)均值:称为随机变量X的均值或数学期望,它反映了离散型随机变量取值的平均水平.
(2)方差:称为随机变量X的方差,它刻画了随机变量X与其均值的平均偏离程度,并称为随机变量X的标准差,记为.
5.均值与方差的性质
(1).
(2).
6.两点分布的均值、方差
若X服从两点分布,则.
7.条件概率及其性质
(1)一般地,设A,B为两个事件,且,称为在事件A发生的条件下,事件B发生的概率.
(2)条件概率的性质:
(i);
(ii)如果B和C是两个互斥事件,则.
8.全概率公式
一般地,设是一组两两互斥的事件,,且,则对任意的事件,有,称此公式为全概率公式.
9.二项分布的均值与方差:若,则,.
10.正态曲线的定义:
函数(其中实数和为参数)的图象为正态分布密度曲线,简称正态曲线.
11.正态分布的定义及表示:
如果对于任何实数,随机变量X满足,则称X的分布为正态分布,记作.
典型例题
1.环境空气质量监测资料表明,某地一天的空气质量为轻度污染的概率是0.25,连续两天为轻度污染的概率是0.1,则此地在某天的空气质量为轻度污染的条件下,随后一天的空气质量也为轻度污染的概率是( )
A.0.4 B.0.25 C.0.1 D.0.05
2.通讯中常采取重复发送信号的办法来减少在接收中可能发生的错误,假定接收一个信号时发生错误的概率是,为减少错误,采取每一个信号连发3次,接收时以“少数服从多数”的原则判断,则判错一个信号的概率为( )
A. B. C. D.
3.若随机变量X的分布列为
X 0 1
P 0.2 m
已知随机变量,且,则a与b的值为( )
A. B. C. D.
4.一批产品分为一,二,三3个等级,其中一级品的个数是二级品的两倍,三级品的个数是二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量,则__________.
5.已知服从正态分布的随机变量在区间内取值的概率分别为0.683,0.954,0.997.若某种袋装大米的质量X(单位:)服从正态分布,任意选一袋这种大米,质量在的概率为_________________.
6.为进一步激发青少年学习中华优秀传统文化的热情,某校举办了“我爱古诗词”对抗赛,在每轮对抗赛中,高二年级胜高三年级的概率为,高一年级胜高三年级的概率为,且每轮对抗赛的成绩互不影响.
(1)若高二年级与高三年级进行4轮对抗赛,求高三年级在对抗赛中至少有3轮胜出的概率;
(2)若高一年级与高三年级进行对抗,高一年级胜2轮就停止,否则开始新一轮对抗,但对抗不超过5轮,求对抗赛轮数X的分布列与数学期望.
答案以及解析
1.答案:A
解析:设事件A:一天的空气质量为轻度污染,事件B:随后一天的空气质量也为轻度污染,由题知,所以.故选A.
2.答案:B
解析:得到正确信号的概率有两种情形,一种情形是三次接收正确,概率为,另一种情形是两次接收正确,一次接收不正确,概率为,所以判错一个信号的概率为,故选B.
3.答案:C
解析:由随机变量X的分布列可知,,
,,
,,
,,,故选C.
4.答案:
解析:设二级品有k个,则一级品有个,三级品有个,总数为个,则级别的分布列为
1 2 3
P
.
5.答案:0.818 5
解析:根据题意得到质量在到之间的大米概率为0.954,则小于的大米的概率为;质量在到之间的大米的概率为0.683,故质量大于的大米的概率为.故质量在的大米的概率为.
6.答案:(1)
(2)分布列见解析,
解析:(1)由题意知,高三年级胜高二年级的概率为.
设高三年级在4轮对抗赛中有x轮胜出,“至少有3轮胜出”的概率为P,
则.
(2)由题意知,对抗赛轮数X的所有可能取值为2,3,4,5,
则,
,
,
,
故X的分布列为
X 2 3 4 5
P
.
第四步:单元核心素养对接高考
核心素养
离散型随机变量及其分布列、均值与方差是高考的热点,常以实际问题为背景,与计数原理、古典概型等知识相结合,考查离散型随机变量的分布列、均值和方差,要特别注意二项分布与超几何分布问题及利用期望与方差决策的问题,主要以解答题的形式呈现,难度中等,近两年难度有加大的趋势,更加重视对考生的实际应用能力的考查,要重视对实际问题背景的分析与了解,要在审题、转化、建模等问题上下功夫,重视与其他知识的综合应用.
二项分布及其应用、正态分布是高考的热点,主要考查:①条件概率、相互独立事件的概率的求法,一般以选择题、填空题的形式出现,有时也会渗透在解答题中;②独立重复试验、二项分布、正态分布的应用,结合实际问题以解答题的形式出现.解题时注意对相关概念的理解及相关公式的应用.主要考查考生的数据分析能力.
真题对接
1.【2021年 新高考ⅠⅠ卷,6】某物理量的测量结果服从正态分布,则下列结论中不正确的是( )
A.σ越小,该物理量一次测量结果落在内的概率越大
B.σ越小,该物理量一次测量结果大于10的概率为0.5
C.σ越小,该物理量一次测量结果大于10.01与小于9.99的概率相等
D.σ越小,该物理量一次测量结果落在内的概率与落在内的概率相等
2.【2022年 新高考ⅠⅠ卷,19】在某地区进行流行病调查,随机调查了100名某种疾病患者的年龄,得到如下的样本数据频率分布直方图.
(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值作代表);
(2)估计该地区一位这种疾病患者的年龄位于区间的概率;
(3)已知该地区这种疾病的患病率为0.1%,该地区年龄位于区间的人口占该地区总人口的16%,从该地区中任选一人,若此人的年龄位于区间,求此人患这种疾病的概率(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001).
3.【2021年 新高考Ⅰ卷,18】某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题 并说明理由.
答案以及解析
1.答案:D
解析:本题考查正态曲线的特点.根据正态曲线可直接得出B项, C项正确;越小,则正态曲线越“瘦高”,该物理量一次测量结果落在内的概率越大,A项正确;同理,落在内的概率大于落在内的概率,D项错误.
2.解析:(1)估计该地区这种疾病患者的平均年龄.
(2)解法一由于患者的年龄位于区间是由患者的年龄位于区间,,,,组成的,且相互独立,
所以所求概率.
解法二由于患者的年龄位于区间是由患者的年龄位于区间,,,,组成的,且相互独立,
所以所求概率.
(3)设从该地区任选一人,年龄位于区间为事件A,患这种疾病为事件B,
则,
由频率分布直方图知这种疾病患者年龄位于区间的概率为,
结合该地区这种疾病的患病率为0.1%,可得,
所以从该地区任选一人,若年龄位于区间,
则此人患这种疾病的概率为.
3.解析:(1)X的所有可能取值为0,20,100.
,
,
,
所以X的分布列为
X 0 20 100
P 0.2 0.32 0.48
(2)假设先答B类问题,记Y为小明的累计得分,
则Y的所有可能取值为0,80,100.
,
,
,
所以Y的分布列为
Y 0 80 100
P 0.4 0.12 0.48
所以,
由(1)可知.
因为,
所以为使累计得分的期望最大,小明应选择先回答B类问题.
