2.4.2圆的一般方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共23张PPT)
文档属性
| 名称 | 2.4.2圆的一般方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 20:47:34 | ||
图片预览








文档简介
(共23张PPT)
2.4.2 圆的一般方程
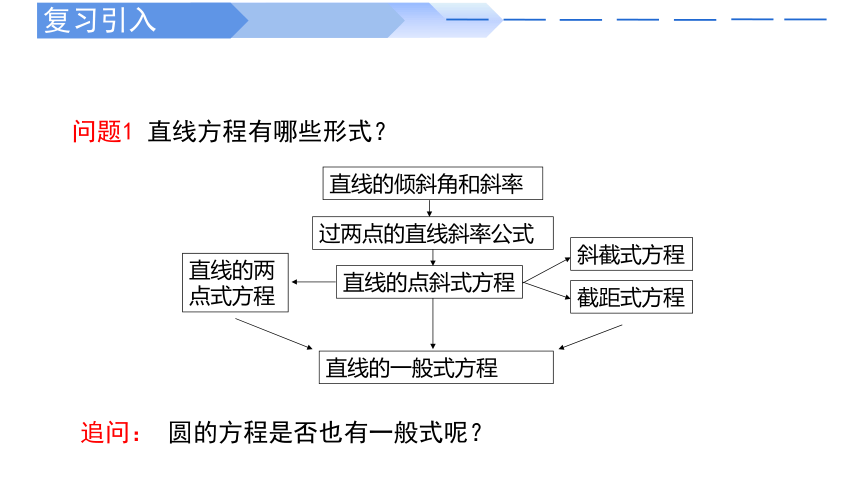
问题1 直线方程有哪些形式?
直线的一般式方程
直线的倾斜角和斜率
直线的两
点式方程
直线的点斜式方程
过两点的直线斜率公式
斜截式方程
截距式方程
复习引入
l
追问: 圆的方程是否也有一般式呢?
前面我们已讨论了圆的标准方程为(x-a)2+(y-b)2=r2,现将其展开
可得:x2+y2-2ax-2bx+a2+b2-r2=0.可见,任何一个圆的方程都可以变形x2+y2+Dx+Ey+F=0的形式.
请大家思考一下,形如x2+y2+Dx+Ey+F=0的方程表示的曲线是不是圆 下面我们来探讨这一方面的问题.
问题导学
新知探究
例如,对于方程对其进行配方,得,因为任意一点的坐标 都不满足这个方程,所以这个方程不表示任何图形,所以形如x2+y2+Dx+Ey+F=0的方程不一定能通过恒等变换为圆的标准方程,这表明形如x2+y2+Dx+Ey+F=0的方程不一定是圆的方程.
问题思考
新知探究
探究新知
将方程x2+y2+Dx+Ey+F=0,配方可得
一、圆的一般方程
新知探究
3.二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆需要满足哪些条件
小试牛刀
1.圆x2+y2-6x=0的圆心坐标是 .
答案:(3,0)
2. 若方程x2+y2+Dx+Ey+F=0表示以(2,-4)为圆心,以4为半径的圆,
则F= .
答案:4
答案:(1)A=C,且均不为0; (2)B=0;(3)D2+E2-4AF>0.
小练
二元二次方程表示圆的判断方法
任何一个圆的方程都可化为x2+y2+Dx+Ey+F=0的形式,但形如x2+y2+Dx+Ey+F=0的方程不一定表示圆.判断它是否表示圆可以有以下两种方法:
(1)计算D2+E2-4F,若其值为正,则表示圆;若其值为0,则表示一个点;若其值为负,则不表示任何图形.
归纳总结
新知探究
问题 圆的标准方程与圆的一般方程各有什么特点呢?
标准方程 一般方程
方程
代数特征 平方和 特殊的二元二次方程
系数
圆心 (a,b)
半径 r
新知探究
l
新知探索
答案:√,×,√.
辨析1.判断正误.
(1)圆的一般方程可以化为圆的标准方程.( )
(2)二元二次方程一定是某个圆的方程.( )
(3)方程表示圆.( )
答案:D.
辨析2.圆的圆心坐标是( ).
A. B. C. D.
例析
例4.求过三点,的圆的方程,并求出这个圆的圆心坐标和半径.
解:设圆的方程是.①
∵,,三点都在圆上,所以它们的坐标都是方程①的解.把它们的坐标依次代入方程①,得到关于的一个三元一次方程组
解这个方程组,得
所以,所求圆的方程是.
由前面的讨论可知,所求圆的圆心坐标是,
半径.
问题 什么是待定系数法?如何运用待定系数法求圆的方程呢?
一般先写出含有未知系数的解的形式(如一种类型的方程、算式或表达式),然后再根据问题所给的条件解得所设的未知系数.由于其中的系数是未知和待定的,这类方法就被称为待定系数法.
新知探究
l
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于 或 的方程组;
(3)解出 或 ,得到标准方程或一般方程.
例析
例5.已知线段的端点的坐标是,端点在圆上运动,求线段的中点的轨迹方程.
解:设点的坐标是,点的坐标是.由于点的坐标
是,且是线段的中点,所以
于是有,. ①
因为点在圆上运动,所以点的坐标满足圆的
方程,即. ② 把①代入②,
得,整理,得.
这就是点的轨迹方程,它表示以为圆心,半径为的圆.
练习
题型一:对圆一般方程的理解
例1.若方程表示圆,求:
(1)实数的取值范围;
(2)圆心坐标和半径.
解:(1)据题意知,
即,解得,
故的取值范围为.
(2)将方程写成标准方程为,
故圆心坐标为,半径.
练习
方法技巧:
方程表示圆的判断方法
(1)配方法.对形如的一元二次方程可以通过配方变形成“标准”形式后,观察是否表示圆.
(2)运用圆的一般方程的判断方法求解.即通过判断是否为正,确定它是否表示圆.
练习
变1.已知,方程表示圆,则圆心坐标为________,半径为________.
答案:,.
解:由圆的一般方程的形式知,解得或.
当时,该方程可化为,
∵,∴不符合题意.
当时,方程可化为,即,
∴圆心坐标为,半径为.
练习
题型二:求圆的一般方程
例2.已知一圆过,两点,且在轴上截得的线段长为,求圆的方程.
解:设圆的方程为,将的坐标分别代入上式,
得令,得,③
由已知,其中,是方程③的两根.
∴.④
联立解得,或
故所求圆的方程为或.
练习
方法技巧:
待定系数法求圆的一般方程的步骤
(1)根据题意设所求的圆的一般方程为;
(2)根据已知条件,建立关于的方程组;
(3)解此方程组,求出的值;
(4)将所得的值代回所设的圆的方程中,就得到所求的圆的一般方程.
练习
变2.求圆心在直线上,且过点和的圆的一般方程.
解:设所求圆的一般方程为,则圆心为.
∵圆心在直线上,∴.
又∵点和在圆上,
∴.
.③
解③组成的方程组,得.
∴所求圆的一般方程为.
练习
题型三:与圆有关的轨迹方程问题
例3.已知圆心为的圆经过点和,且圆心在直线上.
(1)求圆的方程;
解:(1)设点为线段的中点,直线为线段的垂直平分线,则.
又,所以,
所以直线的方程为,即.
由得圆心,
则半径,
所以圆的方程为.
练习
例3.已知圆心为的圆经过点和,且圆心在直线上.
(2)线段的端点的坐标是,端点在圆上运动,求线段的中点的轨迹方程.
解:(2)设
∵点的坐标为,∴即
又点在圆上运动,
∴,即.
整理得.
即所求线段的中点的轨迹方程为.
练习
方法技巧:
求轨迹方程的三种常用方法
(1)直接法:根据题目条件,建立坐标系,设出动点坐标,找出动点满足的条件,然后化简、证明.
(2)定义法:当动点的运动轨迹符合圆的定义时,可利用定义写出动点的轨迹方程.
(3)代入法:若动点依赖于某圆上的一个动点而运动,把用表示,再将点的坐标代入到已知圆的方程中,得点的轨迹方程.
练习
变3.点是圆上的定点,点是圆内一点,为圆上的动点.
(1)求线段的中点的轨迹方程;
(2)若,求线段的中点的轨迹方程.
解:(1)设线段的中点为,由中点公式得点坐标为.
∵点在圆上,∴,
故线段的中点的轨迹方程为.
(2)设线段的中点为,在中,.
设为坐标原点,连接,则,
∴,
∴,
故线段的中点的轨迹方程为.
课堂小结
1.圆的一般方程的概念:
当时,二次方程叫做圆的一般方程.
.圆的一般方程对应的圆心和半径
圆的一般方程表示的圆以为圆心,以为半径长.
2.4.2 圆的一般方程
问题1 直线方程有哪些形式?
直线的一般式方程
直线的倾斜角和斜率
直线的两
点式方程
直线的点斜式方程
过两点的直线斜率公式
斜截式方程
截距式方程
复习引入
l
追问: 圆的方程是否也有一般式呢?
前面我们已讨论了圆的标准方程为(x-a)2+(y-b)2=r2,现将其展开
可得:x2+y2-2ax-2bx+a2+b2-r2=0.可见,任何一个圆的方程都可以变形x2+y2+Dx+Ey+F=0的形式.
请大家思考一下,形如x2+y2+Dx+Ey+F=0的方程表示的曲线是不是圆 下面我们来探讨这一方面的问题.
问题导学
新知探究
例如,对于方程对其进行配方,得,因为任意一点的坐标 都不满足这个方程,所以这个方程不表示任何图形,所以形如x2+y2+Dx+Ey+F=0的方程不一定能通过恒等变换为圆的标准方程,这表明形如x2+y2+Dx+Ey+F=0的方程不一定是圆的方程.
问题思考
新知探究
探究新知
将方程x2+y2+Dx+Ey+F=0,配方可得
一、圆的一般方程
新知探究
3.二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆需要满足哪些条件
小试牛刀
1.圆x2+y2-6x=0的圆心坐标是 .
答案:(3,0)
2. 若方程x2+y2+Dx+Ey+F=0表示以(2,-4)为圆心,以4为半径的圆,
则F= .
答案:4
答案:(1)A=C,且均不为0; (2)B=0;(3)D2+E2-4AF>0.
小练
二元二次方程表示圆的判断方法
任何一个圆的方程都可化为x2+y2+Dx+Ey+F=0的形式,但形如x2+y2+Dx+Ey+F=0的方程不一定表示圆.判断它是否表示圆可以有以下两种方法:
(1)计算D2+E2-4F,若其值为正,则表示圆;若其值为0,则表示一个点;若其值为负,则不表示任何图形.
归纳总结
新知探究
问题 圆的标准方程与圆的一般方程各有什么特点呢?
标准方程 一般方程
方程
代数特征 平方和 特殊的二元二次方程
系数
圆心 (a,b)
半径 r
新知探究
l
新知探索
答案:√,×,√.
辨析1.判断正误.
(1)圆的一般方程可以化为圆的标准方程.( )
(2)二元二次方程一定是某个圆的方程.( )
(3)方程表示圆.( )
答案:D.
辨析2.圆的圆心坐标是( ).
A. B. C. D.
例析
例4.求过三点,的圆的方程,并求出这个圆的圆心坐标和半径.
解:设圆的方程是.①
∵,,三点都在圆上,所以它们的坐标都是方程①的解.把它们的坐标依次代入方程①,得到关于的一个三元一次方程组
解这个方程组,得
所以,所求圆的方程是.
由前面的讨论可知,所求圆的圆心坐标是,
半径.
问题 什么是待定系数法?如何运用待定系数法求圆的方程呢?
一般先写出含有未知系数的解的形式(如一种类型的方程、算式或表达式),然后再根据问题所给的条件解得所设的未知系数.由于其中的系数是未知和待定的,这类方法就被称为待定系数法.
新知探究
l
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于 或 的方程组;
(3)解出 或 ,得到标准方程或一般方程.
例析
例5.已知线段的端点的坐标是,端点在圆上运动,求线段的中点的轨迹方程.
解:设点的坐标是,点的坐标是.由于点的坐标
是,且是线段的中点,所以
于是有,. ①
因为点在圆上运动,所以点的坐标满足圆的
方程,即. ② 把①代入②,
得,整理,得.
这就是点的轨迹方程,它表示以为圆心,半径为的圆.
练习
题型一:对圆一般方程的理解
例1.若方程表示圆,求:
(1)实数的取值范围;
(2)圆心坐标和半径.
解:(1)据题意知,
即,解得,
故的取值范围为.
(2)将方程写成标准方程为,
故圆心坐标为,半径.
练习
方法技巧:
方程表示圆的判断方法
(1)配方法.对形如的一元二次方程可以通过配方变形成“标准”形式后,观察是否表示圆.
(2)运用圆的一般方程的判断方法求解.即通过判断是否为正,确定它是否表示圆.
练习
变1.已知,方程表示圆,则圆心坐标为________,半径为________.
答案:,.
解:由圆的一般方程的形式知,解得或.
当时,该方程可化为,
∵,∴不符合题意.
当时,方程可化为,即,
∴圆心坐标为,半径为.
练习
题型二:求圆的一般方程
例2.已知一圆过,两点,且在轴上截得的线段长为,求圆的方程.
解:设圆的方程为,将的坐标分别代入上式,
得令,得,③
由已知,其中,是方程③的两根.
∴.④
联立解得,或
故所求圆的方程为或.
练习
方法技巧:
待定系数法求圆的一般方程的步骤
(1)根据题意设所求的圆的一般方程为;
(2)根据已知条件,建立关于的方程组;
(3)解此方程组,求出的值;
(4)将所得的值代回所设的圆的方程中,就得到所求的圆的一般方程.
练习
变2.求圆心在直线上,且过点和的圆的一般方程.
解:设所求圆的一般方程为,则圆心为.
∵圆心在直线上,∴.
又∵点和在圆上,
∴.
.③
解③组成的方程组,得.
∴所求圆的一般方程为.
练习
题型三:与圆有关的轨迹方程问题
例3.已知圆心为的圆经过点和,且圆心在直线上.
(1)求圆的方程;
解:(1)设点为线段的中点,直线为线段的垂直平分线,则.
又,所以,
所以直线的方程为,即.
由得圆心,
则半径,
所以圆的方程为.
练习
例3.已知圆心为的圆经过点和,且圆心在直线上.
(2)线段的端点的坐标是,端点在圆上运动,求线段的中点的轨迹方程.
解:(2)设
∵点的坐标为,∴即
又点在圆上运动,
∴,即.
整理得.
即所求线段的中点的轨迹方程为.
练习
方法技巧:
求轨迹方程的三种常用方法
(1)直接法:根据题目条件,建立坐标系,设出动点坐标,找出动点满足的条件,然后化简、证明.
(2)定义法:当动点的运动轨迹符合圆的定义时,可利用定义写出动点的轨迹方程.
(3)代入法:若动点依赖于某圆上的一个动点而运动,把用表示,再将点的坐标代入到已知圆的方程中,得点的轨迹方程.
练习
变3.点是圆上的定点,点是圆内一点,为圆上的动点.
(1)求线段的中点的轨迹方程;
(2)若,求线段的中点的轨迹方程.
解:(1)设线段的中点为,由中点公式得点坐标为.
∵点在圆上,∴,
故线段的中点的轨迹方程为.
(2)设线段的中点为,在中,.
设为坐标原点,连接,则,
∴,
∴,
故线段的中点的轨迹方程为.
课堂小结
1.圆的一般方程的概念:
当时,二次方程叫做圆的一般方程.
.圆的一般方程对应的圆心和半径
圆的一般方程表示的圆以为圆心,以为半径长.
