2.2.3直线的一般式方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共26张PPT)
文档属性
| 名称 | 2.2.3直线的一般式方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 20:48:34 | ||
图片预览







文档简介
(共26张PPT)
2.2.3 直线的一般式方程
问题1 四种表示直线的方程
区别:应用条件不同;表达形式不同;
联系:
点斜式方程 斜截式方程 两点式方程 截距式方程
,它们有怎样的区别与联系?
直线上任意点的几何特征
直线的代数表示:直线上点的横纵坐标x,y的关系
复习回顾
l
追问1:以上四种方程在表示直线时有怎样的局限性?
×
×
×
×
×
×
×
√
√
√
√
√
复习回顾
l
问题: 由下列各条件,写出直线的方程,并画出图形.
(1)斜率是1,经过点A(1,8);
(2)在x轴和y轴上的截距分别是-7,7;
(3)经过两点P1(-1,6),P2(2,9);
(4)在y轴上的截距是7,倾斜角是45°.
问题导学
同学们,请根据前面我们学习的直线方程形式,分别利用点斜式、截距式、两点式和斜截式,求出对应的4个直线方程;
新知探究
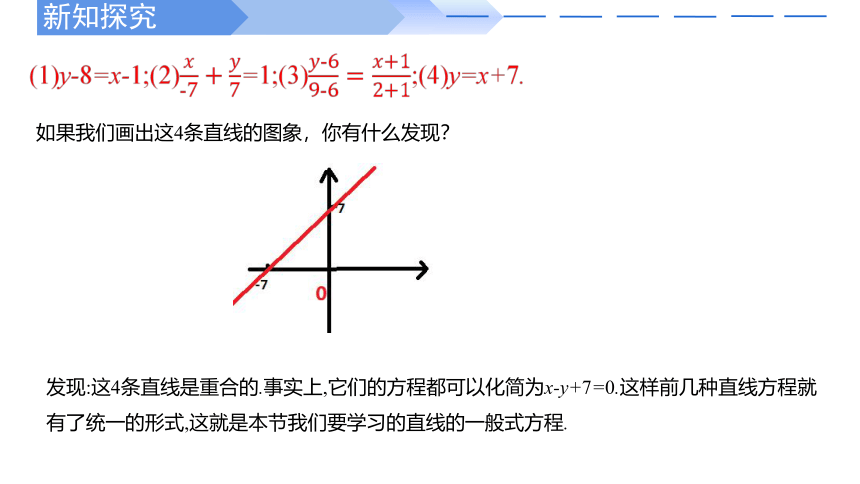
发现:这4条直线是重合的.事实上,它们的方程都可以化简为x-y+7=0.这样前几种直线方程就有了统一的形式,这就是本节我们要学习的直线的一般式方程.
如果我们画出这4条直线的图象,你有什么发现?
新知探究
二元一次方程
一条直线
探究新知
新知探究
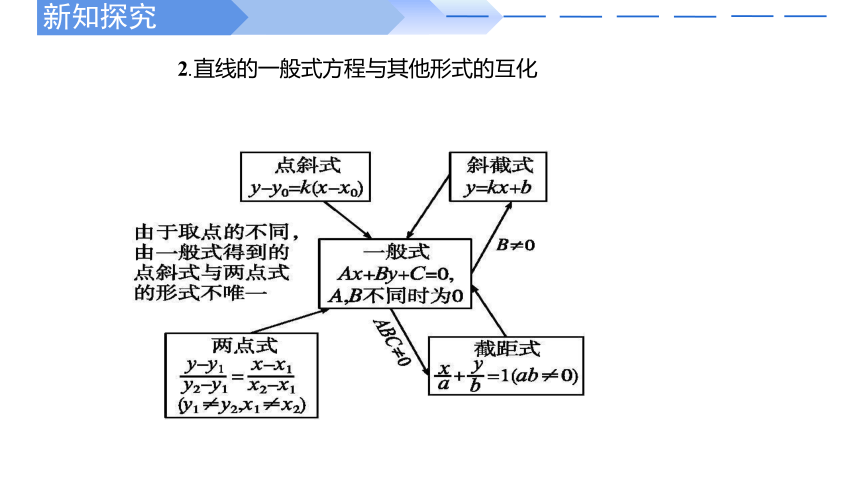
2.直线的一般式方程与其他形式的互化
新知探究
1.在方程Ax+By+C=0(A,B不同时为零)中,A,B,C为何值时,方程表示的直线
(1)平行于x轴;(2)平行于y轴;(3)与x轴重合;(4)与y轴重合.
小试牛刀
新知探究
2.直线方程2x+3y+1=0化为斜截式为 ;
化为截距式为 .
新知探究
3.两条直线的位置关系
新知探究
新知探究
l
例析
例5.已知直线过点,斜率为,求直线的点斜式和一般式方程.
解:经过点,斜率为的直线的
点斜式方程是,
化为一般式,得.
例析
例6.把直线的一般式方程化为斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.
解:把直线的一般式方程化为斜截式.
因此,直线的斜率,它在轴上的截距是.
在直线的方程中,令,得,
即直线在轴上的截距是.
由上面可得直线与轴、轴的交点分别为,,
过,两点作直线,就得直线(如图).
练习
题型一:直线的一般式方程
例1.根据下列条件分别写出直线的方程,并化为一般式方程:
(1)斜率是,且经过点;
(2)斜率是,在轴上的截距为;
解:(1)由点斜式,得直线方程为,
即.
(2)由斜截式,得直线方程为,
即.
练习
例1.根据下列条件分别写出直线的方程,并化为一般式方程:
(3)经过点两,点;
(4)在轴,轴上的截距分别为,;
(5)经过点,且平行于轴.
解:(3)由两点式,得直线方程为,
即.
(4)由截距式,得直线方程为,
即.
(5).
练习
方法技巧:
求直线一般式方程的策略
(1)当时,方程可化为,只需求的值;若,则方程可化为,只需确定,的值.因此,只要给出两个条件,就可以求出直线方程.
(2)在求直线方程时,设一般式方程有时并不简单,常用的还是根据给定条件选用四种特殊形式之一求方程,然后可以转化为一般式.
练习
变1.已知直线经过点,,求直线的点斜式、斜截式和一般式方程,并根据方程指出直线在轴、轴上的截距.
解:∵,所以点斜式方程为,
斜截式方程为,
一般式方程为,
直线在轴上的截距为,在轴上的截距为.
练习
题型二:一般式下的平行与垂直问题
例2.(1)已知直线与直线平行,求的值;
解:(1)由,知:
①当时,显然与不平行;
②当时,,需.
解得或,
∴的值为或.
练习
例2.(2)当为何值时,直线与直线互相垂直?
解:(2)由题意知,直线.
①若1,即时,直线与直线显然垂直.
②若1即时,直线与直线不垂直.
③若1且,则直线,的斜率都存在,
,.当时,即解得综上可知,当或时,直线.
练习
方法技巧:
(1)直线:,直线:,
①若且(或).
②若.
(2)与直线平行的直线方程可设为,与直线垂直的直线方程可设为.
练习
变2.已知直线的方程为求满足下列条件的直线的方程.
(1)过点,且与平行;
(2)过点,且与垂直.
解:(1)由与平行,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
(2)由与垂直,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
练习
题型三:含参数的一般式方程问题
例3.已知直线.
(1)求证:不论为何值,直线总经过第一象限;
(1)证明:将直线的方程整理为,
∴直线的斜率为,且过定点,
而点在第一象限内,故不论为何值,恒过第一象限.
练习
例3.已知直线.
(2)为使直线不经过第二象限,求的取值范围.
(2)解:直线的斜率为.
如图所示,要使不经过第二象限,需斜率,
∴,即的取值范围为.
练习
方法技巧:
直线恒过定点的求解策略
(1)将方程化为点斜式,求得定点的坐标;
(2)将方程变形,把,看作参数的系数,因为此式子对于任意的参数的值都成立,故需系数为零,解方程组可得,的值,即为直线过的定点.
练习
变3.已知直线.若直线不经过第二象限,求的取值范围.
解:①当,即时,直线方程为,该直线不经过第二象限,满足要求.
②当,即时,直线化为截距式方程,
因为直线不过第二象限,故该直线的斜率大于等于零,且在轴的截距小于等于零,即解得所以.
由①②可得,的取值范围为.
课堂小结
直线的一般式方程
(1)定义:关于的二元一次方程(其中不同时为0)叫做直线的一般式方程,简称一般式.
(2)适用范围:平面直角坐标系中,任何一条直线都可用一般式表示.
【注】系数的几何意义:
(1)当时,则(斜率),(轴上的截距);
(2)当,时,则(轴上的截距),此时斜率不存在.
2.2.3 直线的一般式方程
问题1 四种表示直线的方程
区别:应用条件不同;表达形式不同;
联系:
点斜式方程 斜截式方程 两点式方程 截距式方程
,它们有怎样的区别与联系?
直线上任意点的几何特征
直线的代数表示:直线上点的横纵坐标x,y的关系
复习回顾
l
追问1:以上四种方程在表示直线时有怎样的局限性?
×
×
×
×
×
×
×
√
√
√
√
√
复习回顾
l
问题: 由下列各条件,写出直线的方程,并画出图形.
(1)斜率是1,经过点A(1,8);
(2)在x轴和y轴上的截距分别是-7,7;
(3)经过两点P1(-1,6),P2(2,9);
(4)在y轴上的截距是7,倾斜角是45°.
问题导学
同学们,请根据前面我们学习的直线方程形式,分别利用点斜式、截距式、两点式和斜截式,求出对应的4个直线方程;
新知探究
发现:这4条直线是重合的.事实上,它们的方程都可以化简为x-y+7=0.这样前几种直线方程就有了统一的形式,这就是本节我们要学习的直线的一般式方程.
如果我们画出这4条直线的图象,你有什么发现?
新知探究
二元一次方程
一条直线
探究新知
新知探究
2.直线的一般式方程与其他形式的互化
新知探究
1.在方程Ax+By+C=0(A,B不同时为零)中,A,B,C为何值时,方程表示的直线
(1)平行于x轴;(2)平行于y轴;(3)与x轴重合;(4)与y轴重合.
小试牛刀
新知探究
2.直线方程2x+3y+1=0化为斜截式为 ;
化为截距式为 .
新知探究
3.两条直线的位置关系
新知探究
新知探究
l
例析
例5.已知直线过点,斜率为,求直线的点斜式和一般式方程.
解:经过点,斜率为的直线的
点斜式方程是,
化为一般式,得.
例析
例6.把直线的一般式方程化为斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.
解:把直线的一般式方程化为斜截式.
因此,直线的斜率,它在轴上的截距是.
在直线的方程中,令,得,
即直线在轴上的截距是.
由上面可得直线与轴、轴的交点分别为,,
过,两点作直线,就得直线(如图).
练习
题型一:直线的一般式方程
例1.根据下列条件分别写出直线的方程,并化为一般式方程:
(1)斜率是,且经过点;
(2)斜率是,在轴上的截距为;
解:(1)由点斜式,得直线方程为,
即.
(2)由斜截式,得直线方程为,
即.
练习
例1.根据下列条件分别写出直线的方程,并化为一般式方程:
(3)经过点两,点;
(4)在轴,轴上的截距分别为,;
(5)经过点,且平行于轴.
解:(3)由两点式,得直线方程为,
即.
(4)由截距式,得直线方程为,
即.
(5).
练习
方法技巧:
求直线一般式方程的策略
(1)当时,方程可化为,只需求的值;若,则方程可化为,只需确定,的值.因此,只要给出两个条件,就可以求出直线方程.
(2)在求直线方程时,设一般式方程有时并不简单,常用的还是根据给定条件选用四种特殊形式之一求方程,然后可以转化为一般式.
练习
变1.已知直线经过点,,求直线的点斜式、斜截式和一般式方程,并根据方程指出直线在轴、轴上的截距.
解:∵,所以点斜式方程为,
斜截式方程为,
一般式方程为,
直线在轴上的截距为,在轴上的截距为.
练习
题型二:一般式下的平行与垂直问题
例2.(1)已知直线与直线平行,求的值;
解:(1)由,知:
①当时,显然与不平行;
②当时,,需.
解得或,
∴的值为或.
练习
例2.(2)当为何值时,直线与直线互相垂直?
解:(2)由题意知,直线.
①若1,即时,直线与直线显然垂直.
②若1即时,直线与直线不垂直.
③若1且,则直线,的斜率都存在,
,.当时,即解得综上可知,当或时,直线.
练习
方法技巧:
(1)直线:,直线:,
①若且(或).
②若.
(2)与直线平行的直线方程可设为,与直线垂直的直线方程可设为.
练习
变2.已知直线的方程为求满足下列条件的直线的方程.
(1)过点,且与平行;
(2)过点,且与垂直.
解:(1)由与平行,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
(2)由与垂直,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
练习
题型三:含参数的一般式方程问题
例3.已知直线.
(1)求证:不论为何值,直线总经过第一象限;
(1)证明:将直线的方程整理为,
∴直线的斜率为,且过定点,
而点在第一象限内,故不论为何值,恒过第一象限.
练习
例3.已知直线.
(2)为使直线不经过第二象限,求的取值范围.
(2)解:直线的斜率为.
如图所示,要使不经过第二象限,需斜率,
∴,即的取值范围为.
练习
方法技巧:
直线恒过定点的求解策略
(1)将方程化为点斜式,求得定点的坐标;
(2)将方程变形,把,看作参数的系数,因为此式子对于任意的参数的值都成立,故需系数为零,解方程组可得,的值,即为直线过的定点.
练习
变3.已知直线.若直线不经过第二象限,求的取值范围.
解:①当,即时,直线方程为,该直线不经过第二象限,满足要求.
②当,即时,直线化为截距式方程,
因为直线不过第二象限,故该直线的斜率大于等于零,且在轴的截距小于等于零,即解得所以.
由①②可得,的取值范围为.
课堂小结
直线的一般式方程
(1)定义:关于的二元一次方程(其中不同时为0)叫做直线的一般式方程,简称一般式.
(2)适用范围:平面直角坐标系中,任何一条直线都可用一般式表示.
【注】系数的几何意义:
(1)当时,则(斜率),(轴上的截距);
(2)当,时,则(轴上的截距),此时斜率不存在.
