10.1.3古典概型课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册(共17张PPT)
文档属性
| 名称 | 10.1.3古典概型课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 20:49:39 | ||
图片预览






文档简介
(共17张PPT)
10.1.3 古典概型
学习目标
1. 理解古典概型概念及其概率计算公式.
2.会用列举法、树状图法和表格法计算随机事件所含的基本事件数及事件发生的概率.
情境引入
我们讨论过彩票摇号试验、抛掷一枚均匀硬币的试验及掷一枚质地均匀骰子的试验。它们的共同特征有哪些?
有限性:样本空间的样本点只有有限个;
等可能性:每个样本点发生的可能性相等.
新知探究
随机试验E的样本点和样本空间具有如下特征:
(1)等可能性:每个样本点发生的可能性相同.
(2)有限性:样本空间的样本点只有有限个.
则将该随机试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.
古典概型
特点:有限+等可能
新知探究
例1
下列试验中是古典概型的是( )
A.在适宜的条件下,种下一粒种子,观察它是否发芽
B.口袋里有2个白球和2个黑球,这4个球除颜色外其他完全相同,从中任取一球
C.向一个圆面内随机地投一个点,该点落在圆内任意一点都是等可能的
D.射击运动员向一靶心进行射击,试验结果为命中10环,命中9环,…,命中0环
新知探究
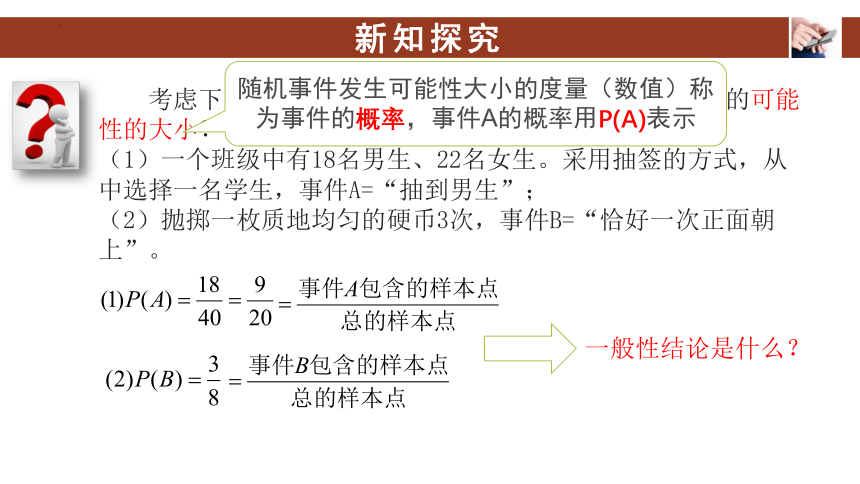
考虑下面两个随机试验,如何度量事件A和事件B发生的可能性的大小?
(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中选择一名学生,事件A=“抽到男生”;
(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”。
一般性结论是什么?
随机事件发生可能性大小的度量(数值)称为事件的概率,事件A的概率用P(A)表示
新知探究
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,
事件A包含其中k个样本点,则定义事件A的概率P(A)=,
其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
古典概型的概率计算公式
新知探究
例2 单选题是标准化考试中常用的题型,一般是从A、B、C、D四个选项中选择一个正确答案.如果考生掌握了考察的内容,它可以选择唯一正确的答案.假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
变式:不定项选择题从A、B、C、D四个选项中选出所有正确答案,同学们可能有一种感觉,如果不知道正确答案,更难猜对,试求不定项选择题猜对的概率.
新知探究
例3 掷两颗质地均匀的骰子(标记为1号和2号),求观察两枚骰子分别可能出现的基本结果.
(1)写出这个试验的样本空间,并判断这个试验是否为古典概型;
(2)求下列事件的概率:A=“两个点数之和为5”;
B=“两个点数相等”; C=“1号骰子的点数大于2号骰子的点数”
解 (1) 抛掷一枚骰子有6种等可能的结果,I号骰子的每一个结果都可以与号骰子的任意一个结果配对, 组成掷两枚骰子试验的一个结果. 所有结果如下表所示:
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
(4,1)
(3,2)
(2,3)
(1,4)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
新知探究
(2) 求出下列事件的概率:A =“两点之和是5”;
B =“两个点数相等”; C =“Ⅰ号骰子的点数大于Ⅱ号骰子的点数.
解
思考:在例3中,为什么要把两枚骰子标上记号?如果不给两枚骰子标记号,会出现什么情况?你能解释其中的原因吗?
新知探究
如果不标上记号,类似于(3,6)和(6,3)的结果将没有区别.
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
(4,1)
(3,2)
为什么结果不一样了?
新知探究
例4 袋子中有5个大小质地完全相同的球,其中2个红球,3个黄球,从中不放回地依次随机摸出2个球,求下列事件的概率:
(1)A=“第一次摸到红球”
(2)B=“第二次摸到红球”
(3)AB=“两次都摸到红球”
解:将2个红球编号为1, 2,三个黄球编号为3, 4, 5. 第一次摸球时有5种等可能的结果, 对应第一次摸球的每一个结果, 第二次摸球时都有4种等可能的结果, 将两次摸球的结果配对, 组成20种等可能的结果, 如下表所示.
新知探究
第一次 第二次
1 2 3 4 5
1 × (1,2) (1,3) (1,4) (1,5)
2 (2,1) × (2,3) (2,4) (2,5)
3 (3,1) (3,2) × (3,4) (3,5)
4 (4,1) (4,2) (4,3) × (4,5)
5 (5,1) (5,2) (5,3) (5,4) ×
(1) 第一次摸到红球的可能结果有8种(表中第1, 2行),
(2) 第二次摸到红球的可能结果有8种(表中第1,2列),
(3) 事件AB包含2个可能结果, 即AB={(1,2), (2, 1)},
新知探究
例10 从两名男生(记为B1和B2)、两名女生(记为G1和G2)中任意抽取两人.
(1) 分别写出有放回简单随机抽样、不放回简单随机抽样和按性别等比例分层抽样的样本空间.
(2) 在三种抽样方式下,分别计算抽到的两人都是男生的概率.
解: (1) 设第一次抽取的人记为x1, 第二次抽取的人记为x2, 则可用数组(x1, x2)表示样本点.
根据相应的抽样方法可知: 有放回简单随机抽样的样本空间为
Ω1={(B1,B1),(B1,B2),(B1,G1),(B1,G2),(B2,B1),(B2,B2),(B2,G1),(B2,G2),(G1,B1),(G1,B2),(G1,G1),(G1,G2),(G2,B1),(G2,B2),(G2,G1),(G2,G2)}. 共16个样本点.
不放回简单随机抽样的样本空间为
Ω2={(B1,B2),(B1,G1),(B1,G2),(B2,B1),(B2,G1),(B2,G2),(G1,B1),(G1,B2),(G1,G2),(G2,B1),(G2,B2),(G2,G1)}. 共12个样本点.
按性别等比例分层抽样,其样本空间为Ω3={(B1,G1),(B1,G2),(B2,G1),(B2,G2)}.
新知探究
解(2):设事件“抽到两名男生”,则对于有放回简单随机抽样
.
因为抽中样本空间中每一个样本点的可能性都相等,所以这是一个古典概型.因此
对于不放回简单抽样,.因为抽中样本空间中每一个样本点
的可能性都相等,所以这是一个古典概型.
因此
因为按性别等比例分层抽样,不可能抽到两名男生,所以,因此0.
梳理总结
再 见
10.1.3 古典概型
学习目标
1. 理解古典概型概念及其概率计算公式.
2.会用列举法、树状图法和表格法计算随机事件所含的基本事件数及事件发生的概率.
情境引入
我们讨论过彩票摇号试验、抛掷一枚均匀硬币的试验及掷一枚质地均匀骰子的试验。它们的共同特征有哪些?
有限性:样本空间的样本点只有有限个;
等可能性:每个样本点发生的可能性相等.
新知探究
随机试验E的样本点和样本空间具有如下特征:
(1)等可能性:每个样本点发生的可能性相同.
(2)有限性:样本空间的样本点只有有限个.
则将该随机试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.
古典概型
特点:有限+等可能
新知探究
例1
下列试验中是古典概型的是( )
A.在适宜的条件下,种下一粒种子,观察它是否发芽
B.口袋里有2个白球和2个黑球,这4个球除颜色外其他完全相同,从中任取一球
C.向一个圆面内随机地投一个点,该点落在圆内任意一点都是等可能的
D.射击运动员向一靶心进行射击,试验结果为命中10环,命中9环,…,命中0环
新知探究
考虑下面两个随机试验,如何度量事件A和事件B发生的可能性的大小?
(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中选择一名学生,事件A=“抽到男生”;
(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”。
一般性结论是什么?
随机事件发生可能性大小的度量(数值)称为事件的概率,事件A的概率用P(A)表示
新知探究
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,
事件A包含其中k个样本点,则定义事件A的概率P(A)=,
其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
古典概型的概率计算公式
新知探究
例2 单选题是标准化考试中常用的题型,一般是从A、B、C、D四个选项中选择一个正确答案.如果考生掌握了考察的内容,它可以选择唯一正确的答案.假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
变式:不定项选择题从A、B、C、D四个选项中选出所有正确答案,同学们可能有一种感觉,如果不知道正确答案,更难猜对,试求不定项选择题猜对的概率.
新知探究
例3 掷两颗质地均匀的骰子(标记为1号和2号),求观察两枚骰子分别可能出现的基本结果.
(1)写出这个试验的样本空间,并判断这个试验是否为古典概型;
(2)求下列事件的概率:A=“两个点数之和为5”;
B=“两个点数相等”; C=“1号骰子的点数大于2号骰子的点数”
解 (1) 抛掷一枚骰子有6种等可能的结果,I号骰子的每一个结果都可以与号骰子的任意一个结果配对, 组成掷两枚骰子试验的一个结果. 所有结果如下表所示:
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
(4,1)
(3,2)
(2,3)
(1,4)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
新知探究
(2) 求出下列事件的概率:A =“两点之和是5”;
B =“两个点数相等”; C =“Ⅰ号骰子的点数大于Ⅱ号骰子的点数.
解
思考:在例3中,为什么要把两枚骰子标上记号?如果不给两枚骰子标记号,会出现什么情况?你能解释其中的原因吗?
新知探究
如果不标上记号,类似于(3,6)和(6,3)的结果将没有区别.
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
(4,1)
(3,2)
为什么结果不一样了?
新知探究
例4 袋子中有5个大小质地完全相同的球,其中2个红球,3个黄球,从中不放回地依次随机摸出2个球,求下列事件的概率:
(1)A=“第一次摸到红球”
(2)B=“第二次摸到红球”
(3)AB=“两次都摸到红球”
解:将2个红球编号为1, 2,三个黄球编号为3, 4, 5. 第一次摸球时有5种等可能的结果, 对应第一次摸球的每一个结果, 第二次摸球时都有4种等可能的结果, 将两次摸球的结果配对, 组成20种等可能的结果, 如下表所示.
新知探究
第一次 第二次
1 2 3 4 5
1 × (1,2) (1,3) (1,4) (1,5)
2 (2,1) × (2,3) (2,4) (2,5)
3 (3,1) (3,2) × (3,4) (3,5)
4 (4,1) (4,2) (4,3) × (4,5)
5 (5,1) (5,2) (5,3) (5,4) ×
(1) 第一次摸到红球的可能结果有8种(表中第1, 2行),
(2) 第二次摸到红球的可能结果有8种(表中第1,2列),
(3) 事件AB包含2个可能结果, 即AB={(1,2), (2, 1)},
新知探究
例10 从两名男生(记为B1和B2)、两名女生(记为G1和G2)中任意抽取两人.
(1) 分别写出有放回简单随机抽样、不放回简单随机抽样和按性别等比例分层抽样的样本空间.
(2) 在三种抽样方式下,分别计算抽到的两人都是男生的概率.
解: (1) 设第一次抽取的人记为x1, 第二次抽取的人记为x2, 则可用数组(x1, x2)表示样本点.
根据相应的抽样方法可知: 有放回简单随机抽样的样本空间为
Ω1={(B1,B1),(B1,B2),(B1,G1),(B1,G2),(B2,B1),(B2,B2),(B2,G1),(B2,G2),(G1,B1),(G1,B2),(G1,G1),(G1,G2),(G2,B1),(G2,B2),(G2,G1),(G2,G2)}. 共16个样本点.
不放回简单随机抽样的样本空间为
Ω2={(B1,B2),(B1,G1),(B1,G2),(B2,B1),(B2,G1),(B2,G2),(G1,B1),(G1,B2),(G1,G2),(G2,B1),(G2,B2),(G2,G1)}. 共12个样本点.
按性别等比例分层抽样,其样本空间为Ω3={(B1,G1),(B1,G2),(B2,G1),(B2,G2)}.
新知探究
解(2):设事件“抽到两名男生”,则对于有放回简单随机抽样
.
因为抽中样本空间中每一个样本点的可能性都相等,所以这是一个古典概型.因此
对于不放回简单抽样,.因为抽中样本空间中每一个样本点
的可能性都相等,所以这是一个古典概型.
因此
因为按性别等比例分层抽样,不可能抽到两名男生,所以,因此0.
梳理总结
再 见
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
