同构再解析几何中的运用课件-2023届高三数学二轮复习(共32张PPT)
文档属性
| 名称 | 同构再解析几何中的运用课件-2023届高三数学二轮复习(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-31 21:04:14 | ||
图片预览











文档简介
(共32张PPT)
2023届高三数学二轮复习
微专题:同构法在解析几何中的运用
课程标准 核心素养
了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用 数学抽象
直观想象
逻辑推理
数学运算
经历从具体情境中抽象出椭圆的过程,掌握椭圆的定义,标准方程及简单几何性质
了解抛物线与双曲线定义,几何图形和标准方程,以及它们的简单几何性质
通过圆锥曲线与方程的学习,进一步体会数形结合的思想
了解椭圆、抛物线的简单应用
(1)新课标(2017年版2020年修订)解读
新课标
考题 题号 分值 题型 难度 考点 考向
2022新高考I 11 5 多项选择题 中 直线与抛物线 定长、弦长
2022新高考I 14 5 填空题 易 圆 圆的切线方程
2022新高考I 16 5 填空题 难 椭圆 焦点三角形、离心率
2022新高考I 21 12 解答题 难 直线与双曲线 定值问题、面积问题
2021新高考Ⅰ 5 5 单项选择题 中 椭圆定义 与不等式结合考查最值问题
2021新高考Ⅰ 10 5 多项选择题 易 圆 直线与圆上一点的最值问题
2021新高考Ⅰ 14 5 填空题 易 抛物线 准线方程
2021新高考Ⅰ 21 12 解答题 难 直线与双曲线 轨迹方程、弦长、定值问题
2020新高考Ⅰ 9 5 多项选择题 易 曲线方程 圆、椭圆、双曲线、渐近线
2020新高考Ⅰ 13 5 填空题 易 抛物线 焦点弦长问题
2020新高考Ⅰ 15 5 填空题 中 圆 面积问题
2020新高考Ⅰ 22 12 解答题 难 直线与椭圆 标准方程,定值定点问题
三小一大命题规律
真题再现
考题明细
命题特点
命题趋向
考查知识:抛物线方程,准线方程,弦长公式
考查能力:逻辑思维能力、运算求解能力。
学科素养:数学运算、逻辑推理。
真题再现
命题特点
命题趋向
考题明细
考查知识:椭圆定义,结合不等式考最值问题
考查能力:逻辑思维能力、运算求解能力。
学科素养:数学运算、逻辑推理。
真题再现
命题特点
命题趋向
考题明细
考查椭圆、抛物线的定义,弦长。及准线方程
对解析几何基础知识、基本技能、基本思想方法等考查
考查考生逻辑思维能力和运算求解能力
01
02
03
真题再现
命题特点
命题趋向
考题明细
(1)将直线与圆锥曲线的位置关系、圆锥曲线的概念和
几何性质相结合考查;考查了过定点,定值问题;
考查考生逻辑思维能力和运算求解能力。
(2)22年和21年同时考查了双曲线,20年考查了椭圆,
它打破了传统解析几何解答题以椭圆为首,抛物线次之,双曲线再次之的认知。
真题再现
命题特点
命题趋向
考题明细
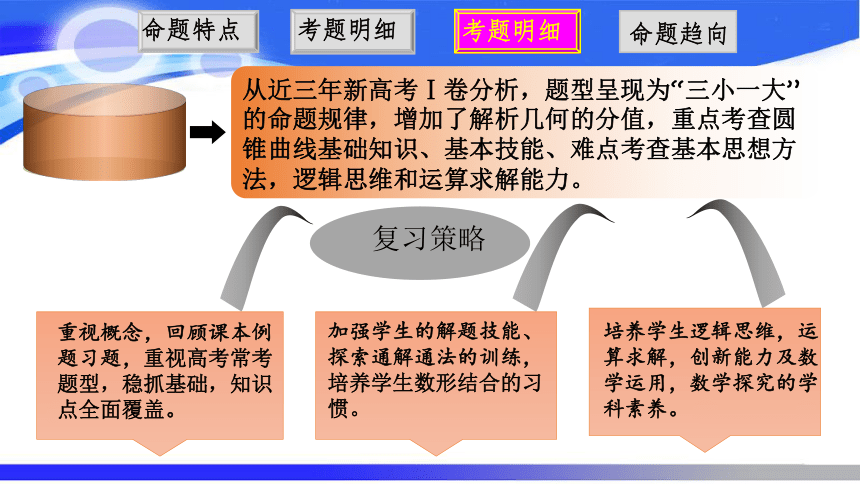
从近三年新高考Ⅰ卷分析,题型呈现为“三小一大”的命题规律,增加了解析几何的分值,重点考查圆锥曲线基础知识、基本技能、难点考查基本思想方法,逻辑思维和运算求解能力。
重视概念,回顾课本例题习题,重视高考常考题型,稳抓基础,知识点全面覆盖。
加强学生的解题技能、探索通解通法的训练,培养学生数形结合的习惯。
培养学生逻辑思维,运算求解,创新能力及数学运用,数学探究的学科素养。
复习策略
考题明细
考题明细
命题特点
命题趋向
1.题量:从近三年新高考Ⅰ卷分析来看,本单元的题量有所增加;大题的难度有所加强,这突出了数学作为基础学科的选拔功能。
2.重点考查内容:椭圆、抛物线、双曲线在20年、21年、22年的试题中均有体现,22年、21年连续两年大题均是考查双曲线,那为什么新高考Ⅰ卷连续两年都考了双曲线?是因为双曲线综合类问题一般都会涉及到双曲线标准方程的一支或两支、待定系数法、直线与双曲线的位置关系等知识,此类题型综合性强,计算量大。
考题明细
命题趋势
命题特点
命题特点
3.体现数学思想、考查核心素养.近三年全国Ⅰ卷圆锥曲线中的考题将数形结合思想,函数和方程思想体现的淋漓尽致,突出考查了逻辑推理、数学运算、数学抽象、数学建模等核心素养,23年高考可能还会突出这些思想和素养的考查;
4.知识交汇命制综合题.近三年试题与其它章节知识交汇考查,22年第21题第2问结合三角函数求面积,21年第5题结合基本不等式求最值,有些试题还融入了平面向量等知识点,因此解析几何结合其它章节知识点的这个趋势仍然需要关注
考题明细
命题趋势
命题特点
命题特点
真题再现
真题再现
试题再现
试题再现
复习引入
具有相同的结构。
同构后出现了D点坐标
总结:具有相同结构的式子或条件,可以运用同构思想解题。
(一)点击高考,发现问题
几何问题
代数问题
形助数、数助形
解读条件和结论,选择合理工具,几何特征代数化
(一)点击高考,发现问题
(一)点击高考,发现问题
(一)点击高考,发现问题
(一)点击高考,发现问题
解题思维导图
设
(一)点击高考,发现问题
(一)点击高考,发现问题
结构相同
总结:联立直线方程和同构法都可以解题,但同构思想能优化计算, 直接得出结果。
(二)小组讨论,分析问题
斜率同构
总结:根据题目结果来同构。
(二)小组讨论,分析问题
(二)实战演练,解决问题
思维导图
(二)类比探究,分析问题
方法一
(二)类比探究,分析问题
方法二
总结:巩固同构同构思想在解析几何中的运用。
(五)归纳总结
同构法是处理解析几何对称问题的有力武器.同构思想的介入,使得解析几何中对称问题、切线问题、平行线截线段成比例问题等,结构相同或相似问题的求解过程变得简单明了.
参数同构
斜率同构
切线同构
(六)教学反思
结合近几年高考试题和最近调考试题中同构思想解圆锥曲线问题,我发现对于圆锥曲线大题,学生立马想到联立直线与曲线方程,然而有些解析题采用联立直线会导致计算量大,甚至很难得结果。本节课开始,有些学生不接受同构法,例1,变式训练1,仍然有部分同学采用联立直线,为了让学生真正理解同构解题的本质,经过了细心指导——同构的条件、并在具有相同结构条件下,比较了同构法与传统法的解题过程,发现同构法能优化计算,能直接得出所求结果。引导和对比后,全班学生都接受了同构思想解题。
(五)课后训练
(五)课后训练
目的:巩固同构同构思想在解析几何中的运用。
2023届高三数学二轮复习
微专题:同构法在解析几何中的运用
课程标准 核心素养
了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用 数学抽象
直观想象
逻辑推理
数学运算
经历从具体情境中抽象出椭圆的过程,掌握椭圆的定义,标准方程及简单几何性质
了解抛物线与双曲线定义,几何图形和标准方程,以及它们的简单几何性质
通过圆锥曲线与方程的学习,进一步体会数形结合的思想
了解椭圆、抛物线的简单应用
(1)新课标(2017年版2020年修订)解读
新课标
考题 题号 分值 题型 难度 考点 考向
2022新高考I 11 5 多项选择题 中 直线与抛物线 定长、弦长
2022新高考I 14 5 填空题 易 圆 圆的切线方程
2022新高考I 16 5 填空题 难 椭圆 焦点三角形、离心率
2022新高考I 21 12 解答题 难 直线与双曲线 定值问题、面积问题
2021新高考Ⅰ 5 5 单项选择题 中 椭圆定义 与不等式结合考查最值问题
2021新高考Ⅰ 10 5 多项选择题 易 圆 直线与圆上一点的最值问题
2021新高考Ⅰ 14 5 填空题 易 抛物线 准线方程
2021新高考Ⅰ 21 12 解答题 难 直线与双曲线 轨迹方程、弦长、定值问题
2020新高考Ⅰ 9 5 多项选择题 易 曲线方程 圆、椭圆、双曲线、渐近线
2020新高考Ⅰ 13 5 填空题 易 抛物线 焦点弦长问题
2020新高考Ⅰ 15 5 填空题 中 圆 面积问题
2020新高考Ⅰ 22 12 解答题 难 直线与椭圆 标准方程,定值定点问题
三小一大命题规律
真题再现
考题明细
命题特点
命题趋向
考查知识:抛物线方程,准线方程,弦长公式
考查能力:逻辑思维能力、运算求解能力。
学科素养:数学运算、逻辑推理。
真题再现
命题特点
命题趋向
考题明细
考查知识:椭圆定义,结合不等式考最值问题
考查能力:逻辑思维能力、运算求解能力。
学科素养:数学运算、逻辑推理。
真题再现
命题特点
命题趋向
考题明细
考查椭圆、抛物线的定义,弦长。及准线方程
对解析几何基础知识、基本技能、基本思想方法等考查
考查考生逻辑思维能力和运算求解能力
01
02
03
真题再现
命题特点
命题趋向
考题明细
(1)将直线与圆锥曲线的位置关系、圆锥曲线的概念和
几何性质相结合考查;考查了过定点,定值问题;
考查考生逻辑思维能力和运算求解能力。
(2)22年和21年同时考查了双曲线,20年考查了椭圆,
它打破了传统解析几何解答题以椭圆为首,抛物线次之,双曲线再次之的认知。
真题再现
命题特点
命题趋向
考题明细
从近三年新高考Ⅰ卷分析,题型呈现为“三小一大”的命题规律,增加了解析几何的分值,重点考查圆锥曲线基础知识、基本技能、难点考查基本思想方法,逻辑思维和运算求解能力。
重视概念,回顾课本例题习题,重视高考常考题型,稳抓基础,知识点全面覆盖。
加强学生的解题技能、探索通解通法的训练,培养学生数形结合的习惯。
培养学生逻辑思维,运算求解,创新能力及数学运用,数学探究的学科素养。
复习策略
考题明细
考题明细
命题特点
命题趋向
1.题量:从近三年新高考Ⅰ卷分析来看,本单元的题量有所增加;大题的难度有所加强,这突出了数学作为基础学科的选拔功能。
2.重点考查内容:椭圆、抛物线、双曲线在20年、21年、22年的试题中均有体现,22年、21年连续两年大题均是考查双曲线,那为什么新高考Ⅰ卷连续两年都考了双曲线?是因为双曲线综合类问题一般都会涉及到双曲线标准方程的一支或两支、待定系数法、直线与双曲线的位置关系等知识,此类题型综合性强,计算量大。
考题明细
命题趋势
命题特点
命题特点
3.体现数学思想、考查核心素养.近三年全国Ⅰ卷圆锥曲线中的考题将数形结合思想,函数和方程思想体现的淋漓尽致,突出考查了逻辑推理、数学运算、数学抽象、数学建模等核心素养,23年高考可能还会突出这些思想和素养的考查;
4.知识交汇命制综合题.近三年试题与其它章节知识交汇考查,22年第21题第2问结合三角函数求面积,21年第5题结合基本不等式求最值,有些试题还融入了平面向量等知识点,因此解析几何结合其它章节知识点的这个趋势仍然需要关注
考题明细
命题趋势
命题特点
命题特点
真题再现
真题再现
试题再现
试题再现
复习引入
具有相同的结构。
同构后出现了D点坐标
总结:具有相同结构的式子或条件,可以运用同构思想解题。
(一)点击高考,发现问题
几何问题
代数问题
形助数、数助形
解读条件和结论,选择合理工具,几何特征代数化
(一)点击高考,发现问题
(一)点击高考,发现问题
(一)点击高考,发现问题
(一)点击高考,发现问题
解题思维导图
设
(一)点击高考,发现问题
(一)点击高考,发现问题
结构相同
总结:联立直线方程和同构法都可以解题,但同构思想能优化计算, 直接得出结果。
(二)小组讨论,分析问题
斜率同构
总结:根据题目结果来同构。
(二)小组讨论,分析问题
(二)实战演练,解决问题
思维导图
(二)类比探究,分析问题
方法一
(二)类比探究,分析问题
方法二
总结:巩固同构同构思想在解析几何中的运用。
(五)归纳总结
同构法是处理解析几何对称问题的有力武器.同构思想的介入,使得解析几何中对称问题、切线问题、平行线截线段成比例问题等,结构相同或相似问题的求解过程变得简单明了.
参数同构
斜率同构
切线同构
(六)教学反思
结合近几年高考试题和最近调考试题中同构思想解圆锥曲线问题,我发现对于圆锥曲线大题,学生立马想到联立直线与曲线方程,然而有些解析题采用联立直线会导致计算量大,甚至很难得结果。本节课开始,有些学生不接受同构法,例1,变式训练1,仍然有部分同学采用联立直线,为了让学生真正理解同构解题的本质,经过了细心指导——同构的条件、并在具有相同结构条件下,比较了同构法与传统法的解题过程,发现同构法能优化计算,能直接得出所求结果。引导和对比后,全班学生都接受了同构思想解题。
(五)课后训练
(五)课后训练
目的:巩固同构同构思想在解析几何中的运用。
同课章节目录
