北师大版八年级数学下册 1.1等腰三角形 试题(含答案)
文档属性
| 名称 | 北师大版八年级数学下册 1.1等腰三角形 试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 15:05:48 | ||
图片预览



文档简介
1.1等腰三角形
一、选择题
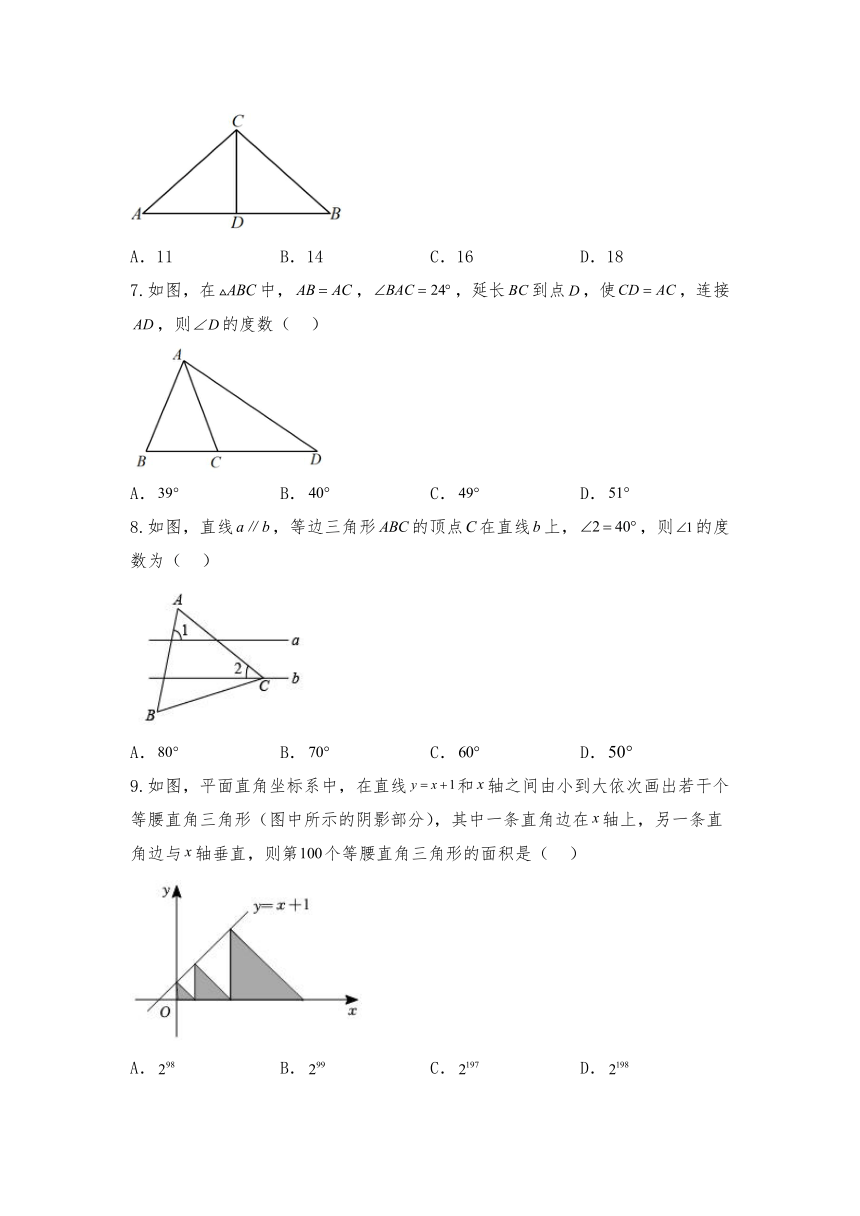
1.如图,,,添加下列一个条件后,不能使的是( )
A. B. C. D.
2.如图,,,,,,则的度数为( )
A. B. C. D.
3.如图,将一个等边三角形剪去一个角后,等于( )
A. B. C. D.
4.等腰三角形是轴对称图形,它的对称轴是( )
A.腰上的中线 B.腰上的高所在的直线
C.顶角的平分线所在的直线 D.过顶点的直线
5.如果等腰三角形的一个内角等于,则它的底角是( )
A. B. C.或 D.或
6.如图,在中,,平分.若,,则的周长为( )
A.11 B.14 C.16 D.18
7.如图,在中,,,延长到点,使,连接,则的度数( )
A. B. C. D.
8.如图,直线,等边三角形的顶点在直线上,,则的度数为( )
A. B. C. D.
9.如图,平面直角坐标系中,在直线和轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在轴上,另一条直角边与轴垂直,则第个等腰直角三角形的面积是( )
A. B. C. D.
二、填空题
1.若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为_____.
2.如图,已知,点D在上,且,则的度数为_____.
3.在中,,若使为正三角形,请你再添一个条件:___________.
4.如图,在等边三角形的边各取一点D,E,连接交于点F,使,若,则长度为_____.
5.如图,在中,,是角平分线,点E、F是上的两点,,,则图中阴影部分的面积之和为 _____.
6.如图,在中,,平分,交于D,,则是____________三角形.
7.如图,在等边三角形中,,是边上的高,延长至点E,使,则的长为______.
8.如图,中,,于点D,点E、F分别在上运动,若的面积为6,则的最小值为______.
9.如图,与是等边三角形,连接、,有以下结论
(1);(2);(3);(4);(5)无论如何改变的度数,与始终全等.其中正确结论的序号为_____
10.如图,是等边三角形,D,E分别是上的点,若,则_____.
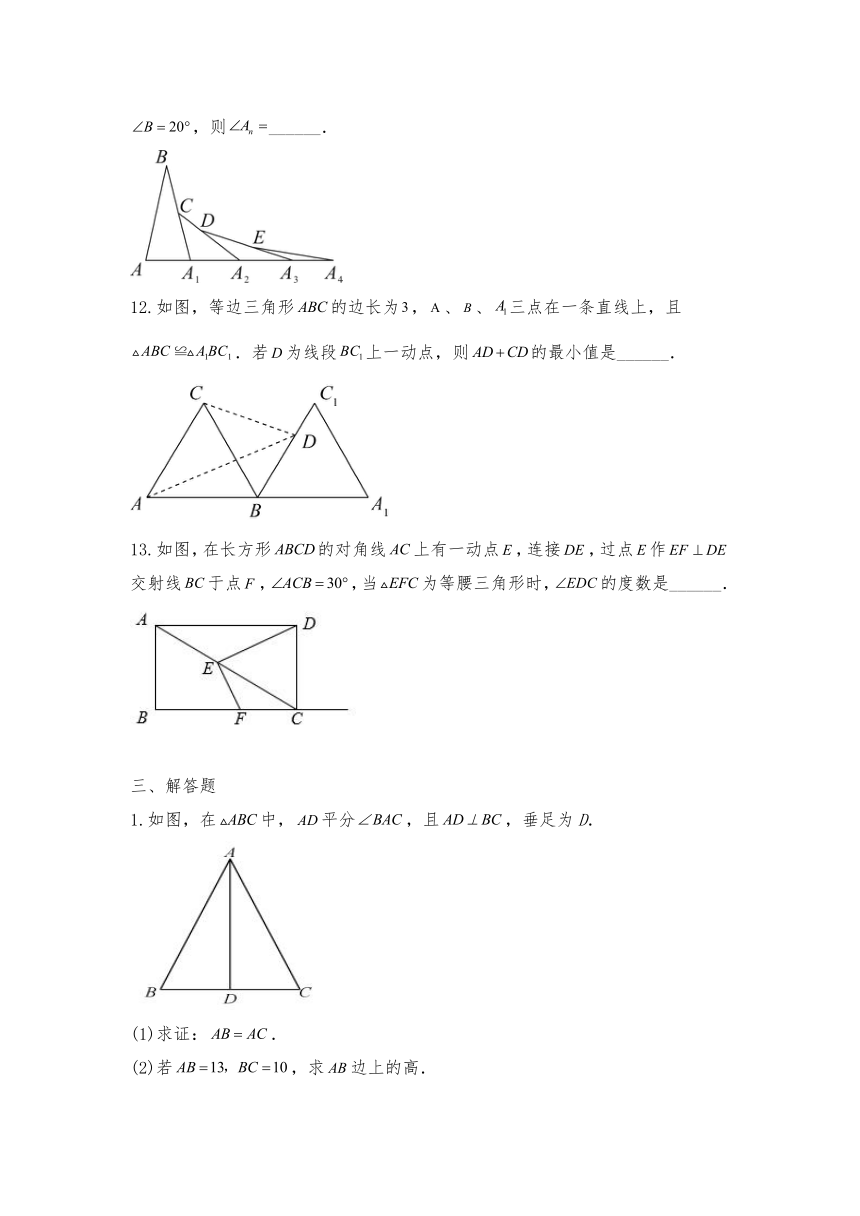
11.如图,已知, …,以此类推,若,则______.
12.如图,等边三角形的边长为,、、三点在一条直线上,且.若为线段上一动点,则的最小值是______.
13.如图,在长方形的对角线上有一动点,连接,过点作交射线于点,,当为等腰三角形时,的度数是______.
三、解答题
1.如图,在中,平分,且,垂足为D.
(1)求证:.
(2)若,求边上的高.
2.如图:在中,,D为边的中点,过点D作于点E,于点F.
(1)求证:;
(2)若,求的周长.
3.如图,在锐角中,点E是边上一点,,于点D,与交于点G.
求证:
(1);
(2)是等腰三角形.
4.如图,是等边三角形,点、、分别在、、上;若,,求证:
(1);
(2)是等边三角形.
5.如图,△ABC是等腰三角形,点D,E分别在腰AC,AB上,且BE=CD,连接BD,CE.求证:BD=CE.
6.如图,在和中,,,,且点D在线段上,连.
(1)求证:;
(2)若,求的度数.
7.如图,是等边三角形,是等腰三角形,且,,以D为顶点作一个60°角,角的两边分别交,边于M,N两点,连接,延长至E,使,连接.
(1)请在横线上写出角的度数,补充的证明过程.
证明:∵是等边三角形,∴_____.
∵,,∴_____.
∴,_____.
∵,∴_____.
即 ;
(2)求证:.
8.和都是等边三角形.
(1)如图①,连接,并延长相交于点,求证:;
(2)如图①,猜想线段之间有怎样的数量关系?并加以证明;
(3)将绕点旋转到图②的位置时,连接,相交于点,连接,猜想线段之间有怎样的数量关系?直接写出结论,不需要证明.
9.如图,在平面直角坐标系中,点,点B在y轴正半轴上,,.
(1)如图1,当时,连接交y轴于点D,写出点C的坐标;
(2)如图2,轴于B且,连接交y轴于一点E,在B点运动的过程中,的长度是否会发生变化?若不变,求出的长度;若变化,请说明理由;
(3)如图3,N在延长线上,过作轴于Q,探究线段、、之间的数量关系,并证明你的结论.
答案
一、选择题
B.B.C.C.D.D.A.A.C.
二、填空题
1.12. 2.. 3.答案不唯一. 4.3. 5.30.
6.等腰. 7.9. 8.3. 9.(1)(2)(4). 10.50.
11.. 12. 13.或.
三、解答题
1.(1)证明:∵平分,
∴,
∵,
∴,
在和中,
,
∴,
∴.
(2)过点C作,垂足为E,
∵,
∴,
在Rt中,,
∴,
∵,
∴,
∴,
∴,
∴边上的高为.
2.(1)证明:连接,
∵,为边的中点,
∴平分,
∴,
∵,,
∴,
又,
∴,
∴;
(2)解: ,,
∴为等边三角形,
∴,
,
∴,
∴,
,
∴,
∴,
∴的周长为.
3.(1)证明:如图,过点E作于点F,
∵,,
∴.
又∵,,
∴,
∴,
∴;
(2)证明:由(1)知:,
∵,
∴,即,
∴,
∴,
∴是等腰三角形.
4.(1)证明:∵是等边三角形,
∴
在和中
∴;
(2)∵,
∴,,
∵
∴
∴是等边三角形.
5.证明:是等腰三角形,
,
在与中,
,
,
.
6.(1)证明:∵,
∴,即.
在与中,
,
∴≌(SAS);
(2)解:由(1)得,
又∵和都是等腰直角三角形,
∴且,
在中∵且
∴,
∴
7.(1)证明:∵是等边三角形,∴.
∵,,∴.
∴,.
∵,∴.
即 ;
(2)∵,,,
∴,
∴,,
∵,
∴,
∵,
∴,
∵,,
∴,
∴,
∵,,
∴.
8.(1)证明:
、都是等边三角形,
,,,
,即,
,
,
,
.
(2)证明:在上截取,连接,
,
,
,,
,
,,
,
是等边三角形,
,
.
(3),理由如下:
如图③,在上截取,连接,
同理得:,
∴,
∵,,
∴,
∴,,
∴,
∴是等边三角形,
∴,
∴.
9.(1)解:如图1,过点C作轴于H.
∵,,
∴,,
∵,
∴,,
∴,
∵,
∴,
∴,,
∴,
∴.
(2)在B点运动过程中,长保持不变,的长为3,
理由:如图2,过C作轴于M.
由(1)可知:,
∴,,
∵是等腰直角三角形,
∴,,
∴,,
在与中,
,
∴,
∴,
∴.
(3).
理由:如图,延长交的延长线于M,过点N作于H,交于K.
∵,,,
∴,
∴,,
∵,,,
∴,
∴,
∴.
一、选择题
1.如图,,,添加下列一个条件后,不能使的是( )
A. B. C. D.
2.如图,,,,,,则的度数为( )
A. B. C. D.
3.如图,将一个等边三角形剪去一个角后,等于( )
A. B. C. D.
4.等腰三角形是轴对称图形,它的对称轴是( )
A.腰上的中线 B.腰上的高所在的直线
C.顶角的平分线所在的直线 D.过顶点的直线
5.如果等腰三角形的一个内角等于,则它的底角是( )
A. B. C.或 D.或
6.如图,在中,,平分.若,,则的周长为( )
A.11 B.14 C.16 D.18
7.如图,在中,,,延长到点,使,连接,则的度数( )
A. B. C. D.
8.如图,直线,等边三角形的顶点在直线上,,则的度数为( )
A. B. C. D.
9.如图,平面直角坐标系中,在直线和轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在轴上,另一条直角边与轴垂直,则第个等腰直角三角形的面积是( )
A. B. C. D.
二、填空题
1.若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为_____.
2.如图,已知,点D在上,且,则的度数为_____.
3.在中,,若使为正三角形,请你再添一个条件:___________.
4.如图,在等边三角形的边各取一点D,E,连接交于点F,使,若,则长度为_____.
5.如图,在中,,是角平分线,点E、F是上的两点,,,则图中阴影部分的面积之和为 _____.
6.如图,在中,,平分,交于D,,则是____________三角形.
7.如图,在等边三角形中,,是边上的高,延长至点E,使,则的长为______.
8.如图,中,,于点D,点E、F分别在上运动,若的面积为6,则的最小值为______.
9.如图,与是等边三角形,连接、,有以下结论
(1);(2);(3);(4);(5)无论如何改变的度数,与始终全等.其中正确结论的序号为_____
10.如图,是等边三角形,D,E分别是上的点,若,则_____.
11.如图,已知, …,以此类推,若,则______.
12.如图,等边三角形的边长为,、、三点在一条直线上,且.若为线段上一动点,则的最小值是______.
13.如图,在长方形的对角线上有一动点,连接,过点作交射线于点,,当为等腰三角形时,的度数是______.
三、解答题
1.如图,在中,平分,且,垂足为D.
(1)求证:.
(2)若,求边上的高.
2.如图:在中,,D为边的中点,过点D作于点E,于点F.
(1)求证:;
(2)若,求的周长.
3.如图,在锐角中,点E是边上一点,,于点D,与交于点G.
求证:
(1);
(2)是等腰三角形.
4.如图,是等边三角形,点、、分别在、、上;若,,求证:
(1);
(2)是等边三角形.
5.如图,△ABC是等腰三角形,点D,E分别在腰AC,AB上,且BE=CD,连接BD,CE.求证:BD=CE.
6.如图,在和中,,,,且点D在线段上,连.
(1)求证:;
(2)若,求的度数.
7.如图,是等边三角形,是等腰三角形,且,,以D为顶点作一个60°角,角的两边分别交,边于M,N两点,连接,延长至E,使,连接.
(1)请在横线上写出角的度数,补充的证明过程.
证明:∵是等边三角形,∴_____.
∵,,∴_____.
∴,_____.
∵,∴_____.
即 ;
(2)求证:.
8.和都是等边三角形.
(1)如图①,连接,并延长相交于点,求证:;
(2)如图①,猜想线段之间有怎样的数量关系?并加以证明;
(3)将绕点旋转到图②的位置时,连接,相交于点,连接,猜想线段之间有怎样的数量关系?直接写出结论,不需要证明.
9.如图,在平面直角坐标系中,点,点B在y轴正半轴上,,.
(1)如图1,当时,连接交y轴于点D,写出点C的坐标;
(2)如图2,轴于B且,连接交y轴于一点E,在B点运动的过程中,的长度是否会发生变化?若不变,求出的长度;若变化,请说明理由;
(3)如图3,N在延长线上,过作轴于Q,探究线段、、之间的数量关系,并证明你的结论.
答案
一、选择题
B.B.C.C.D.D.A.A.C.
二、填空题
1.12. 2.. 3.答案不唯一. 4.3. 5.30.
6.等腰. 7.9. 8.3. 9.(1)(2)(4). 10.50.
11.. 12. 13.或.
三、解答题
1.(1)证明:∵平分,
∴,
∵,
∴,
在和中,
,
∴,
∴.
(2)过点C作,垂足为E,
∵,
∴,
在Rt中,,
∴,
∵,
∴,
∴,
∴,
∴边上的高为.
2.(1)证明:连接,
∵,为边的中点,
∴平分,
∴,
∵,,
∴,
又,
∴,
∴;
(2)解: ,,
∴为等边三角形,
∴,
,
∴,
∴,
,
∴,
∴,
∴的周长为.
3.(1)证明:如图,过点E作于点F,
∵,,
∴.
又∵,,
∴,
∴,
∴;
(2)证明:由(1)知:,
∵,
∴,即,
∴,
∴,
∴是等腰三角形.
4.(1)证明:∵是等边三角形,
∴
在和中
∴;
(2)∵,
∴,,
∵
∴
∴是等边三角形.
5.证明:是等腰三角形,
,
在与中,
,
,
.
6.(1)证明:∵,
∴,即.
在与中,
,
∴≌(SAS);
(2)解:由(1)得,
又∵和都是等腰直角三角形,
∴且,
在中∵且
∴,
∴
7.(1)证明:∵是等边三角形,∴.
∵,,∴.
∴,.
∵,∴.
即 ;
(2)∵,,,
∴,
∴,,
∵,
∴,
∵,
∴,
∵,,
∴,
∴,
∵,,
∴.
8.(1)证明:
、都是等边三角形,
,,,
,即,
,
,
,
.
(2)证明:在上截取,连接,
,
,
,,
,
,,
,
是等边三角形,
,
.
(3),理由如下:
如图③,在上截取,连接,
同理得:,
∴,
∵,,
∴,
∴,,
∴,
∴是等边三角形,
∴,
∴.
9.(1)解:如图1,过点C作轴于H.
∵,,
∴,,
∵,
∴,,
∴,
∵,
∴,
∴,,
∴,
∴.
(2)在B点运动过程中,长保持不变,的长为3,
理由:如图2,过C作轴于M.
由(1)可知:,
∴,,
∵是等腰直角三角形,
∴,,
∴,,
在与中,
,
∴,
∴,
∴.
(3).
理由:如图,延长交的延长线于M,过点N作于H,交于K.
∵,,,
∴,
∴,,
∵,,,
∴,
∴,
∴.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
