八年级数学下册试题 1.4 角平分线-北师大版(含答案)
文档属性
| 名称 | 八年级数学下册试题 1.4 角平分线-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 456.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 15:19:20 | ||
图片预览



文档简介
1.4 角平分线
一、选择题
1.如图.点P是的角平分线上的一点,于点E,已知,则点P到的距离是( )
A.18 B.12 C.6 D.9
2.如图,在中,,根据尺规作图的痕迹,判断以下结论错误的是( )
A. B. C. D.
3.如图,在中,平分,平分,,,则( )
A. B. C. D.
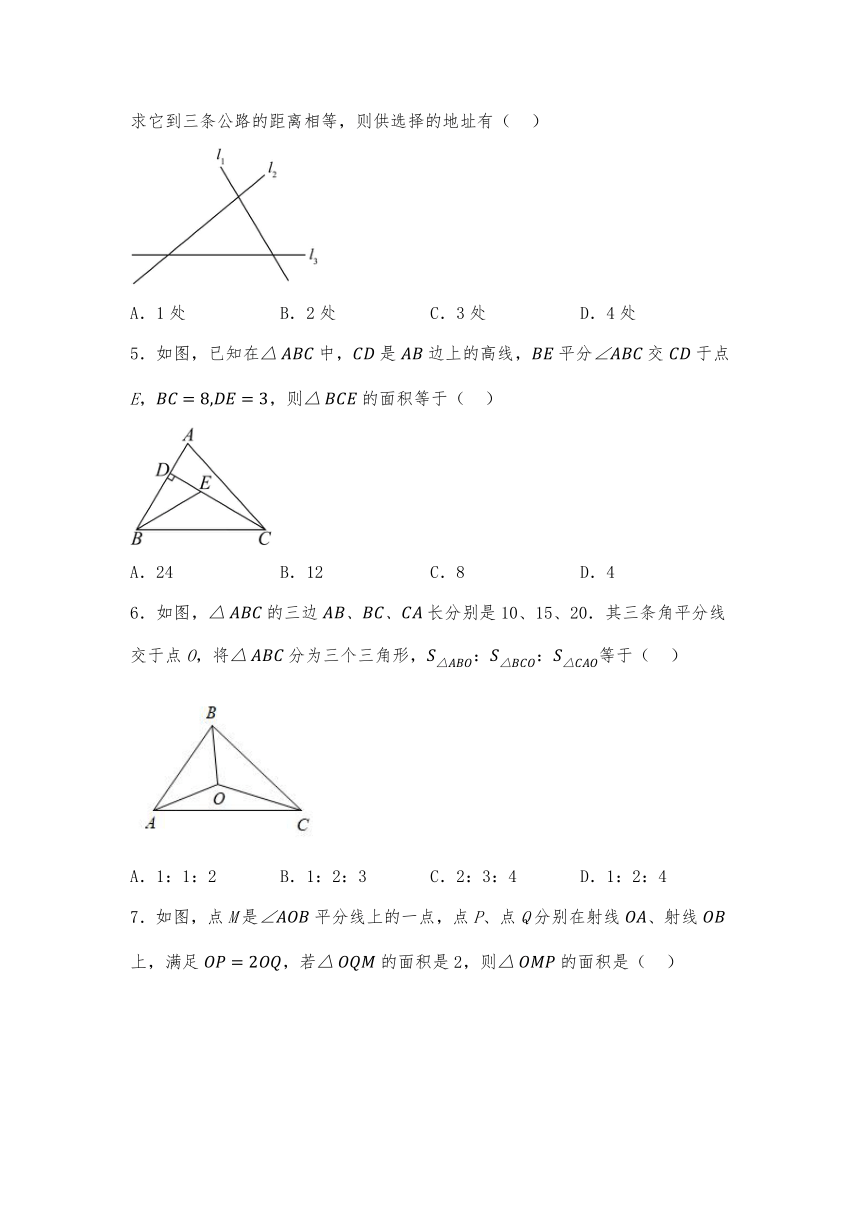
4.如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
5.如图,已知在中,是边上的高线,平分交于点E,,则的面积等于( )
A.24 B.12 C.8 D.4
6.如图,的三边长分别是10、15、20.其三条角平分线交于点O,将分为三个三角形,等于( )
A.1:1:2 B.1:2:3 C.2:3:4 D.1:2:4
7.如图,点M是平分线上的一点,点P、点Q分别在射线、射线上,满足,若的面积是2,则的面积是( )
A.1 B.2 C.3 D.4
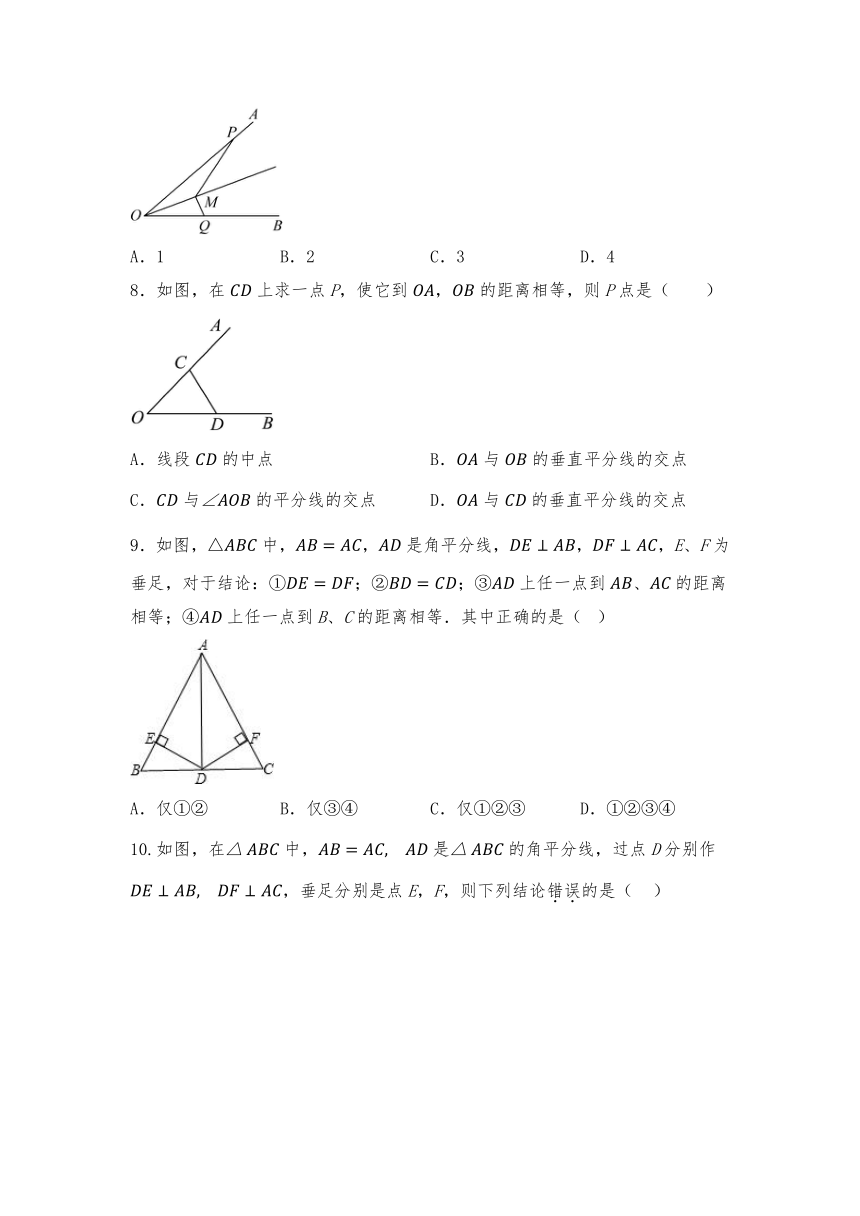
8.如图,在上求一点P,使它到,的距离相等,则P点是( )
A.线段的中点 B.与的垂直平分线的交点
C.与的平分线的交点 D.与的垂直平分线的交点
9.如图,中,,是角平分线,,,E、F为垂足,对于结论:①;②;③上任一点到、的距离相等;④上任一点到B、C的距离相等.其中正确的是( )
A.仅①② B.仅③④ C.仅①②③ D.①②③④
10.如图,在中,是的角平分线,过点D分别作,垂足分别是点E,F,则下列结论错误的是( )
A. B. C. D.
11.如图所示,在中,按下列步骤作图:
第一步:在上分别截取,使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
B.
C. D.
12.如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( )
A.2 B.2 C.4 D.4+2
13.如图,在中,,以B为圆心,适当长为半径画弧交于点M,交于点N,分别以M,N为圆心,大于MN的长为半径画弧,两弧相交于点D,射线交于点E,点F为的中点,连接,若,则的周长是( )
A.8 B. C. D.
二、填空题
1.如图,点是的平分线上的一点,过点作交于点,,若,,则___________
2.如图,在中,点O是内一点,且点O到三边的距离相等,,则的度数为_______°.
3.如图,已知, 平分,为上任意一点,∥,交OB于D,于E.如果,则PE的长为______cm.
4.如图,在中,,平分,交于点,若,则的面积_________.
5.如图,在中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交于点D、E.
②分别以点D、E为圆心,大于 的同样长为半径作弧,两弧交于点F.
③作射线交于点G.
如果,求=________.
6.如图,平分,若,则________.
7.如图,的角平分线与线段的垂直平分线交于点,,,垂足分别为点E、F.若,,则______.
8.如图,在中,,AD平分交BC于点D,在边AB上找一点E,连接DE,使,若,则DE的长为___________.
9.如图:在中,,,,是的角平分线.
(1)则______;
(2)若点是线段上的一个动点,从点以每秒的速度向运动______秒钟后是直角三角形.
三、解答题
1.如图,是的角平分线,分别是和的高,求证:垂直平分.
2.如图在中,,请利用尺规作图法在线段上作一点D,使点D到边的距离等于.(不写作法,保留作图痕迹)
3.如图,在中,,分交于点,过点作交于点,,垂足为点.
(1)求证:;
(2)若,,求的长.
4.如图,在中,,,是的垂直平分线,垂足为点E,交于点D,连接.
(1)求证:平分;
(2)若,求的长.
5.如图,中,是它的角平分线,是上的一点,交与,交与.求证:到的距离与到的距离相等.
6.如图,等腰中,,于点D,点E在线段的左侧且.
(1)求证:;
(2)若点F在的延长线上,求证:平分.
7.已知,如图,在中,的垂直平分线与的角平分线交于点D,
(1)如图1,判断和之间的数量关系,并说明理由;
(2)如图2,若时,探究线段,,之间的数量关系,并说明理由;
答案
一、选择题
D.C.A.D.B.C.D.C.D.C.C.C.D.
二、填空题
1.. 2.. 3. . 4.15. 5.. 6. .
7.1 8.6. 9. 6或
三、解答题
1.证明:∵是的角平分线,分别是和的高,
∴.
∵,
∴,
在和中,
,
∴,
∴.
∴是线段的垂直平分线.
2.解:如图,①以点A为圆心,任意长为半径画弧,交于两点;
②分别以这两点为圆心,大于这两点间的距离为半径画弧,两弧相交于一点;
③连接点A和两弧交点,并延长,延长线与相交于点D,点D即为所求.
3.(1)证明:∵分交于点,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,分交于点,,
∴,
∴,
在中,,
∵,
∴,
在中,.
4.(1)证明:∵是的垂直平分线,
∴,
∴,
∵,
∴,
∴,
∴,
∴平分;
(2)解:∵平分,,
∴,
又∵,
∴.
5.证明:过点D作,
∵是的角平分线,
∴,
∵,,
∴,
∴,即是的角平分线,
∵,
∴,即到的距离与到的距离相等.
6.(1)证明:设交于点I,
∵,,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
(2)证明:作于点G,于点H,则,
在和中,
,
∴,
∴,
∴点A在的平分线上,
∴平分.
7.(1)解:,理由如下:
过点D作于点G, 于点H,如图所示:
的垂直平分线与的角平分线交于点D,
,,
,
,
,
,
,
即,
(2)解:,理由如下:
在上截取,连接,如图所示:
由(1)可知,,
,
,
为等边三角形,
,
,
,
又,
为等边三角形,
,
又,
,
,
在和中,
,
,
,
.
一、选择题
1.如图.点P是的角平分线上的一点,于点E,已知,则点P到的距离是( )
A.18 B.12 C.6 D.9
2.如图,在中,,根据尺规作图的痕迹,判断以下结论错误的是( )
A. B. C. D.
3.如图,在中,平分,平分,,,则( )
A. B. C. D.
4.如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
5.如图,已知在中,是边上的高线,平分交于点E,,则的面积等于( )
A.24 B.12 C.8 D.4
6.如图,的三边长分别是10、15、20.其三条角平分线交于点O,将分为三个三角形,等于( )
A.1:1:2 B.1:2:3 C.2:3:4 D.1:2:4
7.如图,点M是平分线上的一点,点P、点Q分别在射线、射线上,满足,若的面积是2,则的面积是( )
A.1 B.2 C.3 D.4
8.如图,在上求一点P,使它到,的距离相等,则P点是( )
A.线段的中点 B.与的垂直平分线的交点
C.与的平分线的交点 D.与的垂直平分线的交点
9.如图,中,,是角平分线,,,E、F为垂足,对于结论:①;②;③上任一点到、的距离相等;④上任一点到B、C的距离相等.其中正确的是( )
A.仅①② B.仅③④ C.仅①②③ D.①②③④
10.如图,在中,是的角平分线,过点D分别作,垂足分别是点E,F,则下列结论错误的是( )
A. B. C. D.
11.如图所示,在中,按下列步骤作图:
第一步:在上分别截取,使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
B.
C. D.
12.如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( )
A.2 B.2 C.4 D.4+2
13.如图,在中,,以B为圆心,适当长为半径画弧交于点M,交于点N,分别以M,N为圆心,大于MN的长为半径画弧,两弧相交于点D,射线交于点E,点F为的中点,连接,若,则的周长是( )
A.8 B. C. D.
二、填空题
1.如图,点是的平分线上的一点,过点作交于点,,若,,则___________
2.如图,在中,点O是内一点,且点O到三边的距离相等,,则的度数为_______°.
3.如图,已知, 平分,为上任意一点,∥,交OB于D,于E.如果,则PE的长为______cm.
4.如图,在中,,平分,交于点,若,则的面积_________.
5.如图,在中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交于点D、E.
②分别以点D、E为圆心,大于 的同样长为半径作弧,两弧交于点F.
③作射线交于点G.
如果,求=________.
6.如图,平分,若,则________.
7.如图,的角平分线与线段的垂直平分线交于点,,,垂足分别为点E、F.若,,则______.
8.如图,在中,,AD平分交BC于点D,在边AB上找一点E,连接DE,使,若,则DE的长为___________.
9.如图:在中,,,,是的角平分线.
(1)则______;
(2)若点是线段上的一个动点,从点以每秒的速度向运动______秒钟后是直角三角形.
三、解答题
1.如图,是的角平分线,分别是和的高,求证:垂直平分.
2.如图在中,,请利用尺规作图法在线段上作一点D,使点D到边的距离等于.(不写作法,保留作图痕迹)
3.如图,在中,,分交于点,过点作交于点,,垂足为点.
(1)求证:;
(2)若,,求的长.
4.如图,在中,,,是的垂直平分线,垂足为点E,交于点D,连接.
(1)求证:平分;
(2)若,求的长.
5.如图,中,是它的角平分线,是上的一点,交与,交与.求证:到的距离与到的距离相等.
6.如图,等腰中,,于点D,点E在线段的左侧且.
(1)求证:;
(2)若点F在的延长线上,求证:平分.
7.已知,如图,在中,的垂直平分线与的角平分线交于点D,
(1)如图1,判断和之间的数量关系,并说明理由;
(2)如图2,若时,探究线段,,之间的数量关系,并说明理由;
答案
一、选择题
D.C.A.D.B.C.D.C.D.C.C.C.D.
二、填空题
1.. 2.. 3. . 4.15. 5.. 6. .
7.1 8.6. 9. 6或
三、解答题
1.证明:∵是的角平分线,分别是和的高,
∴.
∵,
∴,
在和中,
,
∴,
∴.
∴是线段的垂直平分线.
2.解:如图,①以点A为圆心,任意长为半径画弧,交于两点;
②分别以这两点为圆心,大于这两点间的距离为半径画弧,两弧相交于一点;
③连接点A和两弧交点,并延长,延长线与相交于点D,点D即为所求.
3.(1)证明:∵分交于点,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,分交于点,,
∴,
∴,
在中,,
∵,
∴,
在中,.
4.(1)证明:∵是的垂直平分线,
∴,
∴,
∵,
∴,
∴,
∴,
∴平分;
(2)解:∵平分,,
∴,
又∵,
∴.
5.证明:过点D作,
∵是的角平分线,
∴,
∵,,
∴,
∴,即是的角平分线,
∵,
∴,即到的距离与到的距离相等.
6.(1)证明:设交于点I,
∵,,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
(2)证明:作于点G,于点H,则,
在和中,
,
∴,
∴,
∴点A在的平分线上,
∴平分.
7.(1)解:,理由如下:
过点D作于点G, 于点H,如图所示:
的垂直平分线与的角平分线交于点D,
,,
,
,
,
,
,
即,
(2)解:,理由如下:
在上截取,连接,如图所示:
由(1)可知,,
,
,
为等边三角形,
,
,
,
又,
为等边三角形,
,
又,
,
,
在和中,
,
,
,
.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
