北师大版八年级数学下册试题 第三章 图形的平移与旋转测试卷(含答案)
文档属性
| 名称 | 北师大版八年级数学下册试题 第三章 图形的平移与旋转测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 803.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 15:33:29 | ||
图片预览




文档简介
第三章 图形的平移与旋转测试卷
一、选择题(本大题共14个小题,每题2分,共28分)
1. 2020年4月7日,中国邮政发行了《众志成城 抗击疫情》邮票一套两枚(图1),以此纪念在抗击新冠肺炎疫情的过程中,中国人民所展现出的“中国精神、中国力量、中国担当”.两枚邮票用一个“众”字型的背景图案巧妙相连,从几何的角度看,这个图案(图2)( )
A.是中心对称图形而不是轴对称图形
B.是轴对称图形而不是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
2.在平面直角坐标系中,把点向右平移1个单位后所得的点的坐标是( )
A. B. C. D.
3.在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移
C.平移和旋转 D.旋转和轴对称
4.点关于原点的对称点的坐标是( )
A.(﹣2,﹣3) B.(2,﹣3) C.(2,3) D.(3,﹣2)
5.如图,两个全等的直角三角形重叠在一起,将其中沿着点到的方向平移到的位置,,平移距离为,则的面积为( )
A.6 B.12 C.18 D.24
6.如图,经过平移后得到,下列说法:
①
②
③
④和的面积相等
⑤四边形和四边形的面积相等,其中正确的有( )
A.个 B.个 C.个 D.个
7.在平面直角坐标系中,将直线沿坐标轴方向平移后,得到直线与关于坐标原点中心对称,则下列平移作法正确的是( )
A.将向右平移4个单位长度 B.将向左平移6个单位长度
C.将向上平移6个单位长度 D.将向上平移4个单位长度
8.如图,在中,.将绕点按顺时针方向旋转 度后得到,此时点在边上,斜边交边于点,则图中阴影部分的面积为( )
A.27 B.9 C. D.
9.如图,已知OAB是正三角形,OP⊥OB,OP=OA,将OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
10.如图,在方格纸中,三角形ABC经过变换得到三角形DEF,正确变换的是( )
A.把三角形ABC向下平移4格,再绕着点C逆时针方向旋转
B.把三角形ABC向下平移5格,再绕着点C顺时针方向旋转
C.把三角形ABC绕着点C逆时针方向旋转,再向下平移2格
D.把三角形ABC绕着点C顺时针方向旋转,再向下平移5格
11.如图,点为角平分线交点,,,,将平移使其顶点与重合,则图中阴影部分的周长为( ).
A.4 B.6 C.8 D.10
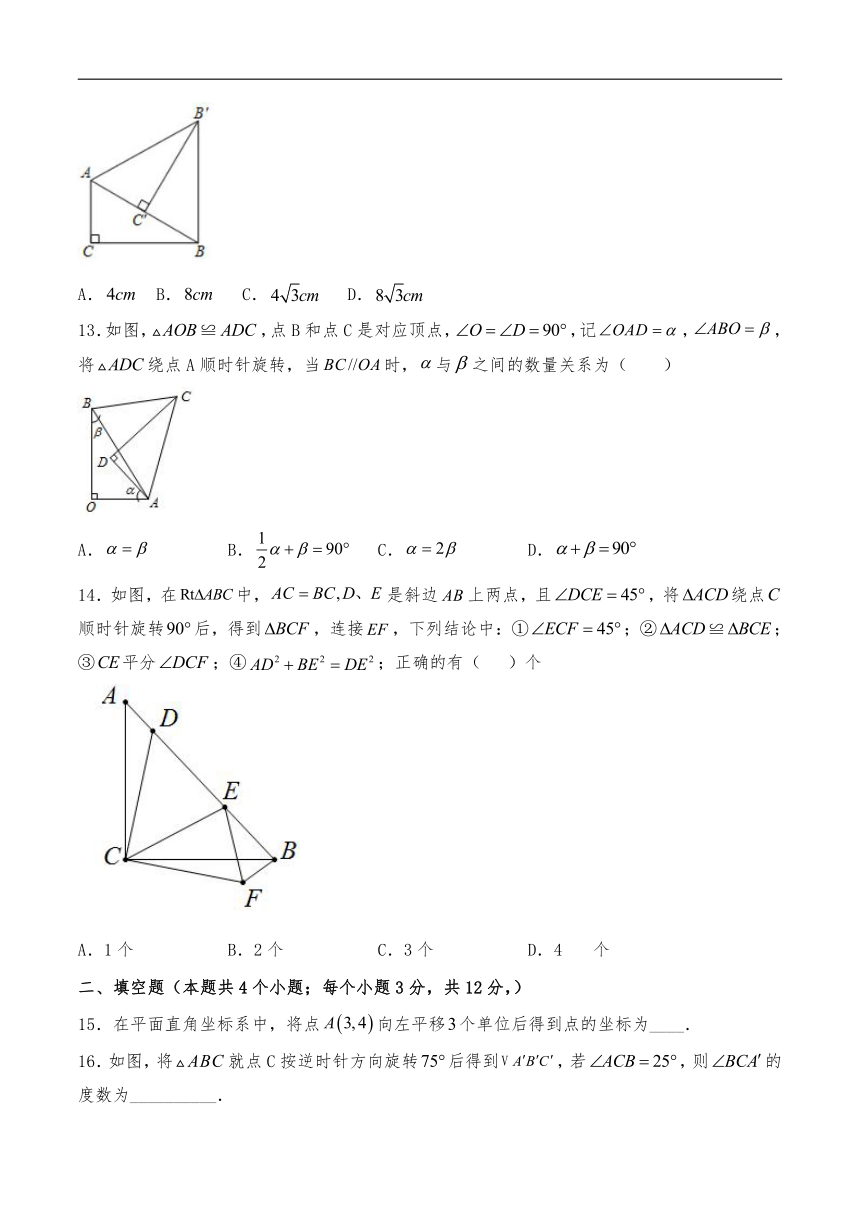
12.如图,在中,将绕点逆时针旋转得到使点落在边上,连接,则的长度是( )
A. B. C. D.
13.如图,,点B和点C是对应顶点,,记,,将绕点A顺时针旋转,当时,与之间的数量关系为( )
A. B. C. D.
14.如图,在中,是斜边上两点,且,将绕点顺时针旋转后,得到,连接,下列结论中:①;②≌;③平分;④;正确的有( )个
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4个小题;每个小题3分,共12分,)
15.在平面直角坐标系中,将点向左平移个单位后得到点的坐标为____.
16.如图,将就点C按逆时针方向旋转后得到,若,则的度数为__________.
17.如图,在平面直角坐标系中,点A,B,C的坐标分别为,,,一个电动玩具从坐标原点O出发,第一次跳跃到点,使得点与点O关于点A成中心对称;第二次跳跃到点,使得点与点关于点B成中心对称;第三次跳跃到点,使得点与点关于点C成中心对称,第四次跳跃到点,使得点与点关于点A成中心对称;第五次跳跃到点,使得点与点关于点B成中心对称……照此规律重复下去,则点的坐标为_________.
18.如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为_____.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在中,,,.将绕点逆时针旋转一个角,得到,点恰好在边上.
(1)求的度数;
(2)求的长.
20.如图①,将线段A1A2向右平移2个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图②中,将折线A1A2A3向右平移2个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移2个单位,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中阴影部分的面积(设长方形水平方向长均为a,竖直方向长均为b):S1=_______,S2=____________,S3=__________;
(3)如图④,一块长方形草地,长为20米,宽为10米,草地上有一条弯曲的小路(小路任何地方的宽度都是2米),请你写出小路部分所占的面积是多少米2;
(4)如图⑤,若在(3)中的草地又有一条横向的弯曲小路(小路任何地方的宽度都是1米),请你写出小路部分所占的面积是多少米2.
21.在平面直角坐标系中,的顶点坐标,.
(1)在图中作出关于轴对称的图形;
(2)在轴上找一点,使最短,在图中标出点的位置(请保留作图痕迹).
(3)将向下平移4个单位长度,得到,点的对应点为点,点的对应点为点,直接写出线段与轴交点的坐标.
22.将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
(1)如图①,当点E在BD上时,求证:FD=CD;
(2)当α为何值时,GC=GB?
23.如图,在平面直角坐标系中,点A,B的坐标分别为(,0),(3,0).现将线段AB向上平移2个单位,再向右平移1个单位,得到线段AB的对应线段CD,连接AC,BD.
(1)点C,D的坐标分别为_______, ________,并求出四边形ABDC的面积S四边形ABDC;
(2)在y轴上存在一点P,连接PA,PB,且S△PAB =S四边形ABDC,求出满足条件的所有点P的坐标.
(3)若点Q为线段BD上一点(不与B,D两点重合),则的值______(填“变”或“不变”).
24.如图所示,在平面直角坐标系中,的三个顶点分别是.
(1)作出与关于原点O成中心对称的;
(2)若点B关于x轴的对称点为点,将点向右平移a个单位长度后落在的内部(不包括顶点和边).
①写出点坐标_________;
②写出a的取值范围为___________.
25.(1)问题发现:
如图1,和均为等边三角形,当旋转至点A,D,E在同一直线上,连接.
①填空:的度数为______.
②线段、之间的数量关系是_______.
(2)拓展研究:
如图2,和均为等腰三角形,且,点A、D、E在同一直线上,若,,求的长度.
(3)探究发现:
图1中的和,在旋转过程中当点A,D,E不在同一直线上时,设直线与相交于点O,试在备用图中探索的度数,直接写出结果,并说明理由.
26.如图1,已知△ABC中,∠ACB=90°,AC=BC=6,点D在AB边的延长线上,且CD=AB.
(1)求BD的长度;
(2)如图2,将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A'CD'.
①若α=30°,A'D'与CD相交于点E,求DE的长度;
②连接A'D、BD',若旋转过程中A'D=BD'时,求满足条件的α的度数.
(3)如图3,将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A'CD',若点M为AC的中点,点N为线段A'D'上任意一点,直接写出旋转过程中线段MN长度的取值范围.
答案
一、选择题
B.D.D.B.A.A.D.D.D.D.C.B.C.C.
二、填空题
15.(0,4). 16.50°. 17.(-2,0). 18.20°或40°.
三、解答题
19.
解:(1)由旋转得到:
∴ ,,
∴
∴,即
(2)在中,
∴=
20.(1)如图.
(2)三个图形中阴影部分的面积都可看作是以b为长,2为宽的长方形的面积,故S1=2b,S2=2b,S3=2b;
(3)小路部分所占的面积是2×10=20米2;
(4)小路部分所占的面积是10×2+20×1-2×1=38米2.
21.
解(1)过点A、B、C作y轴的对称点A1、B1、C1,
顺次连结A1B1、B1C1、C1A1,
则△A1B1C1为所求;
(2)如图,连结AB1交y轴于点P,
则BP=B1P,AP+BP=AP+B1P=AB1,
由两点之间,线段最短,
则点即为所求;
(3) 将向下平移4个单位长度,得到,如图,
∵,
∴点D(-1,1)E(-3,-3)F(-4,-1).
设DF解析式为y=kx+b,
代入得:,
解得:,
DF解析式为,
当y=0时,x=,
Q(,0).
22.
(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,
又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,
又∵DE=ED,
∴△AED≌△FDE(SAS),
∴DF=AE,
又∵AE=AB=CD,
∴CD=DF;
(2)如图,当GB=GC时,点G在BC的垂直平分线上,
分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=AD=AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=60°;
②当点G在AD左侧时,同理可得△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=360°﹣60°=300°.
23.
解:(1)∵将线段AB向上平移2个单位,再向右平移1个单位得到点C、D
又∵点A,B的坐标分别为(,0),(3,0)
∴C(0,2),D(4,2).
由题意可知:四边形ABDC为平行四边形,
∴S四边形ABDC=OC×AB=2×4=8.
(2)当点P在y轴正半轴时,设点P的纵坐标为a,图形如下
根据题意,得×4=8.
解得:a=4
同理当点P在y轴负半轴时,a=-4
∴P(0,4)或P(0,-4).
(3)不变.
图形如下,过点Q作QM∥CD
∵CD是AB平移得到,∴AB∥CD
∵QM∥CD,∴QM∥AB
∴∠DCQ=∠CQM,∠MQO=∠QOB
∴∠DCQ+∠QOB=∠CQM+∠MQO=∠CQO
∴,比值始终不变
24.
解:(1)如图,△A′B′C′即为所求.
(2)①B1(﹣2,1).
②∵A′(3,﹣2),C′(4,2),
∴直线A′C′的解析式为y=4x﹣14,
当y=1时,x=,
,
∴a的取值范围为.
故答案为:.
25.
(1)①如图1,
∵和均为等边三角形,
∴,,,
∴,
在和中,
,
∴,
∴,
∵为等边三角形,
∴,
∵点A,D,E在同一直线上,
∴,
∴,
∴.
故答案为:60°.
②∵,
∴,
故答案为:.
(2)∵和均为等腰直角三角形,
∴,,,
∴,
在和中,
,
∴,
∴,,
∵为等腰直角三角形,
∴,
∵点A,D,E在同一直线上,
∴,
∴,
∴,
∴.
(3)如图3,由(1)知,
∴,
∵,
∴,
∴,
如图4,同理求得,
∴,
∵的度数是60°或120°.
26.解:(1)如图1,过点C作CH⊥AB于H,
∵∠ACB=90°,AC=BC=6,CH⊥AB,
∴AB=CD=6,CH=BH=AB=3,∠CAB=∠CBA=45°,
∴DH=,
∴BD=DH﹣BH=3﹣3;
(2)①如图2,过点E作EF⊥CD'于F,
∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A′CD′,
∴CD=CD'=6,
∵图1中CD=2CH,
∴∠DCD'=30°=∠CDA=∠CD'A',
∴CE=D'E,
又∵EF⊥CD',
∴CF=D'F=3,EF=,CE=2EF=2,
∴DE=DC﹣CE=6﹣2;
②如图2﹣1,
∵∠ABC=45°,∠ADC=30°,
∴∠BCD=15°,
∴∠ACD=105°,
∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A′CD′,
∴AC=A'C,CD=CD',∠ACA'=∠DCD'=α,
∴CB=CA',
又∵A′D=BD′,
∴△A'CD≌△BCD'(SSS),
∴∠A'CD=∠BCD',
∴105°﹣α=15°+α,
∴α=45°;
如图2﹣2,
同理可证:△A'CD≌△BCD',
∴∠A'CD=∠BCD',
∴α﹣105°=360°﹣α﹣15°,
∴α=225°,
综上所述:满足条件的α的度数为45°或225°;
(3)如图3,当A'D'⊥AC时,N是AC与A'D'的交点时,MN的长度最小,
∵∠A'=45°,A'D'⊥AC,
∴∠A'=∠NCA'=45°,
∴CN=A'N=3,
∵点M为AC的中点,
∴CM=AC=3,
∴MN的最小值=NC﹣CM=3﹣3;
如图4,当点A,点C,点D'共线,且点N与点D'重合时,MN有最大值,
此时MN=CM+CN=6+3,
∴线段MN的取值范围是3﹣3≤MN≤6+3.
一、选择题(本大题共14个小题,每题2分,共28分)
1. 2020年4月7日,中国邮政发行了《众志成城 抗击疫情》邮票一套两枚(图1),以此纪念在抗击新冠肺炎疫情的过程中,中国人民所展现出的“中国精神、中国力量、中国担当”.两枚邮票用一个“众”字型的背景图案巧妙相连,从几何的角度看,这个图案(图2)( )
A.是中心对称图形而不是轴对称图形
B.是轴对称图形而不是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
2.在平面直角坐标系中,把点向右平移1个单位后所得的点的坐标是( )
A. B. C. D.
3.在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移
C.平移和旋转 D.旋转和轴对称
4.点关于原点的对称点的坐标是( )
A.(﹣2,﹣3) B.(2,﹣3) C.(2,3) D.(3,﹣2)
5.如图,两个全等的直角三角形重叠在一起,将其中沿着点到的方向平移到的位置,,平移距离为,则的面积为( )
A.6 B.12 C.18 D.24
6.如图,经过平移后得到,下列说法:
①
②
③
④和的面积相等
⑤四边形和四边形的面积相等,其中正确的有( )
A.个 B.个 C.个 D.个
7.在平面直角坐标系中,将直线沿坐标轴方向平移后,得到直线与关于坐标原点中心对称,则下列平移作法正确的是( )
A.将向右平移4个单位长度 B.将向左平移6个单位长度
C.将向上平移6个单位长度 D.将向上平移4个单位长度
8.如图,在中,.将绕点按顺时针方向旋转 度后得到,此时点在边上,斜边交边于点,则图中阴影部分的面积为( )
A.27 B.9 C. D.
9.如图,已知OAB是正三角形,OP⊥OB,OP=OA,将OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
10.如图,在方格纸中,三角形ABC经过变换得到三角形DEF,正确变换的是( )
A.把三角形ABC向下平移4格,再绕着点C逆时针方向旋转
B.把三角形ABC向下平移5格,再绕着点C顺时针方向旋转
C.把三角形ABC绕着点C逆时针方向旋转,再向下平移2格
D.把三角形ABC绕着点C顺时针方向旋转,再向下平移5格
11.如图,点为角平分线交点,,,,将平移使其顶点与重合,则图中阴影部分的周长为( ).
A.4 B.6 C.8 D.10
12.如图,在中,将绕点逆时针旋转得到使点落在边上,连接,则的长度是( )
A. B. C. D.
13.如图,,点B和点C是对应顶点,,记,,将绕点A顺时针旋转,当时,与之间的数量关系为( )
A. B. C. D.
14.如图,在中,是斜边上两点,且,将绕点顺时针旋转后,得到,连接,下列结论中:①;②≌;③平分;④;正确的有( )个
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4个小题;每个小题3分,共12分,)
15.在平面直角坐标系中,将点向左平移个单位后得到点的坐标为____.
16.如图,将就点C按逆时针方向旋转后得到,若,则的度数为__________.
17.如图,在平面直角坐标系中,点A,B,C的坐标分别为,,,一个电动玩具从坐标原点O出发,第一次跳跃到点,使得点与点O关于点A成中心对称;第二次跳跃到点,使得点与点关于点B成中心对称;第三次跳跃到点,使得点与点关于点C成中心对称,第四次跳跃到点,使得点与点关于点A成中心对称;第五次跳跃到点,使得点与点关于点B成中心对称……照此规律重复下去,则点的坐标为_________.
18.如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为_____.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在中,,,.将绕点逆时针旋转一个角,得到,点恰好在边上.
(1)求的度数;
(2)求的长.
20.如图①,将线段A1A2向右平移2个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图②中,将折线A1A2A3向右平移2个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移2个单位,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中阴影部分的面积(设长方形水平方向长均为a,竖直方向长均为b):S1=_______,S2=____________,S3=__________;
(3)如图④,一块长方形草地,长为20米,宽为10米,草地上有一条弯曲的小路(小路任何地方的宽度都是2米),请你写出小路部分所占的面积是多少米2;
(4)如图⑤,若在(3)中的草地又有一条横向的弯曲小路(小路任何地方的宽度都是1米),请你写出小路部分所占的面积是多少米2.
21.在平面直角坐标系中,的顶点坐标,.
(1)在图中作出关于轴对称的图形;
(2)在轴上找一点,使最短,在图中标出点的位置(请保留作图痕迹).
(3)将向下平移4个单位长度,得到,点的对应点为点,点的对应点为点,直接写出线段与轴交点的坐标.
22.将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
(1)如图①,当点E在BD上时,求证:FD=CD;
(2)当α为何值时,GC=GB?
23.如图,在平面直角坐标系中,点A,B的坐标分别为(,0),(3,0).现将线段AB向上平移2个单位,再向右平移1个单位,得到线段AB的对应线段CD,连接AC,BD.
(1)点C,D的坐标分别为_______, ________,并求出四边形ABDC的面积S四边形ABDC;
(2)在y轴上存在一点P,连接PA,PB,且S△PAB =S四边形ABDC,求出满足条件的所有点P的坐标.
(3)若点Q为线段BD上一点(不与B,D两点重合),则的值______(填“变”或“不变”).
24.如图所示,在平面直角坐标系中,的三个顶点分别是.
(1)作出与关于原点O成中心对称的;
(2)若点B关于x轴的对称点为点,将点向右平移a个单位长度后落在的内部(不包括顶点和边).
①写出点坐标_________;
②写出a的取值范围为___________.
25.(1)问题发现:
如图1,和均为等边三角形,当旋转至点A,D,E在同一直线上,连接.
①填空:的度数为______.
②线段、之间的数量关系是_______.
(2)拓展研究:
如图2,和均为等腰三角形,且,点A、D、E在同一直线上,若,,求的长度.
(3)探究发现:
图1中的和,在旋转过程中当点A,D,E不在同一直线上时,设直线与相交于点O,试在备用图中探索的度数,直接写出结果,并说明理由.
26.如图1,已知△ABC中,∠ACB=90°,AC=BC=6,点D在AB边的延长线上,且CD=AB.
(1)求BD的长度;
(2)如图2,将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A'CD'.
①若α=30°,A'D'与CD相交于点E,求DE的长度;
②连接A'D、BD',若旋转过程中A'D=BD'时,求满足条件的α的度数.
(3)如图3,将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A'CD',若点M为AC的中点,点N为线段A'D'上任意一点,直接写出旋转过程中线段MN长度的取值范围.
答案
一、选择题
B.D.D.B.A.A.D.D.D.D.C.B.C.C.
二、填空题
15.(0,4). 16.50°. 17.(-2,0). 18.20°或40°.
三、解答题
19.
解:(1)由旋转得到:
∴ ,,
∴
∴,即
(2)在中,
∴=
20.(1)如图.
(2)三个图形中阴影部分的面积都可看作是以b为长,2为宽的长方形的面积,故S1=2b,S2=2b,S3=2b;
(3)小路部分所占的面积是2×10=20米2;
(4)小路部分所占的面积是10×2+20×1-2×1=38米2.
21.
解(1)过点A、B、C作y轴的对称点A1、B1、C1,
顺次连结A1B1、B1C1、C1A1,
则△A1B1C1为所求;
(2)如图,连结AB1交y轴于点P,
则BP=B1P,AP+BP=AP+B1P=AB1,
由两点之间,线段最短,
则点即为所求;
(3) 将向下平移4个单位长度,得到,如图,
∵,
∴点D(-1,1)E(-3,-3)F(-4,-1).
设DF解析式为y=kx+b,
代入得:,
解得:,
DF解析式为,
当y=0时,x=,
Q(,0).
22.
(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,
又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,
又∵DE=ED,
∴△AED≌△FDE(SAS),
∴DF=AE,
又∵AE=AB=CD,
∴CD=DF;
(2)如图,当GB=GC时,点G在BC的垂直平分线上,
分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=AD=AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=60°;
②当点G在AD左侧时,同理可得△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=360°﹣60°=300°.
23.
解:(1)∵将线段AB向上平移2个单位,再向右平移1个单位得到点C、D
又∵点A,B的坐标分别为(,0),(3,0)
∴C(0,2),D(4,2).
由题意可知:四边形ABDC为平行四边形,
∴S四边形ABDC=OC×AB=2×4=8.
(2)当点P在y轴正半轴时,设点P的纵坐标为a,图形如下
根据题意,得×4=8.
解得:a=4
同理当点P在y轴负半轴时,a=-4
∴P(0,4)或P(0,-4).
(3)不变.
图形如下,过点Q作QM∥CD
∵CD是AB平移得到,∴AB∥CD
∵QM∥CD,∴QM∥AB
∴∠DCQ=∠CQM,∠MQO=∠QOB
∴∠DCQ+∠QOB=∠CQM+∠MQO=∠CQO
∴,比值始终不变
24.
解:(1)如图,△A′B′C′即为所求.
(2)①B1(﹣2,1).
②∵A′(3,﹣2),C′(4,2),
∴直线A′C′的解析式为y=4x﹣14,
当y=1时,x=,
,
∴a的取值范围为.
故答案为:.
25.
(1)①如图1,
∵和均为等边三角形,
∴,,,
∴,
在和中,
,
∴,
∴,
∵为等边三角形,
∴,
∵点A,D,E在同一直线上,
∴,
∴,
∴.
故答案为:60°.
②∵,
∴,
故答案为:.
(2)∵和均为等腰直角三角形,
∴,,,
∴,
在和中,
,
∴,
∴,,
∵为等腰直角三角形,
∴,
∵点A,D,E在同一直线上,
∴,
∴,
∴,
∴.
(3)如图3,由(1)知,
∴,
∵,
∴,
∴,
如图4,同理求得,
∴,
∵的度数是60°或120°.
26.解:(1)如图1,过点C作CH⊥AB于H,
∵∠ACB=90°,AC=BC=6,CH⊥AB,
∴AB=CD=6,CH=BH=AB=3,∠CAB=∠CBA=45°,
∴DH=,
∴BD=DH﹣BH=3﹣3;
(2)①如图2,过点E作EF⊥CD'于F,
∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A′CD′,
∴CD=CD'=6,
∵图1中CD=2CH,
∴∠DCD'=30°=∠CDA=∠CD'A',
∴CE=D'E,
又∵EF⊥CD',
∴CF=D'F=3,EF=,CE=2EF=2,
∴DE=DC﹣CE=6﹣2;
②如图2﹣1,
∵∠ABC=45°,∠ADC=30°,
∴∠BCD=15°,
∴∠ACD=105°,
∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A′CD′,
∴AC=A'C,CD=CD',∠ACA'=∠DCD'=α,
∴CB=CA',
又∵A′D=BD′,
∴△A'CD≌△BCD'(SSS),
∴∠A'CD=∠BCD',
∴105°﹣α=15°+α,
∴α=45°;
如图2﹣2,
同理可证:△A'CD≌△BCD',
∴∠A'CD=∠BCD',
∴α﹣105°=360°﹣α﹣15°,
∴α=225°,
综上所述:满足条件的α的度数为45°或225°;
(3)如图3,当A'D'⊥AC时,N是AC与A'D'的交点时,MN的长度最小,
∵∠A'=45°,A'D'⊥AC,
∴∠A'=∠NCA'=45°,
∴CN=A'N=3,
∵点M为AC的中点,
∴CM=AC=3,
∴MN的最小值=NC﹣CM=3﹣3;
如图4,当点A,点C,点D'共线,且点N与点D'重合时,MN有最大值,
此时MN=CM+CN=6+3,
∴线段MN的取值范围是3﹣3≤MN≤6+3.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
