八年级数学下册试题 第一章 三角形的证明单元测试卷-北师大版(含答案)
文档属性
| 名称 | 八年级数学下册试题 第一章 三角形的证明单元测试卷-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 979.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 15:39:39 | ||
图片预览


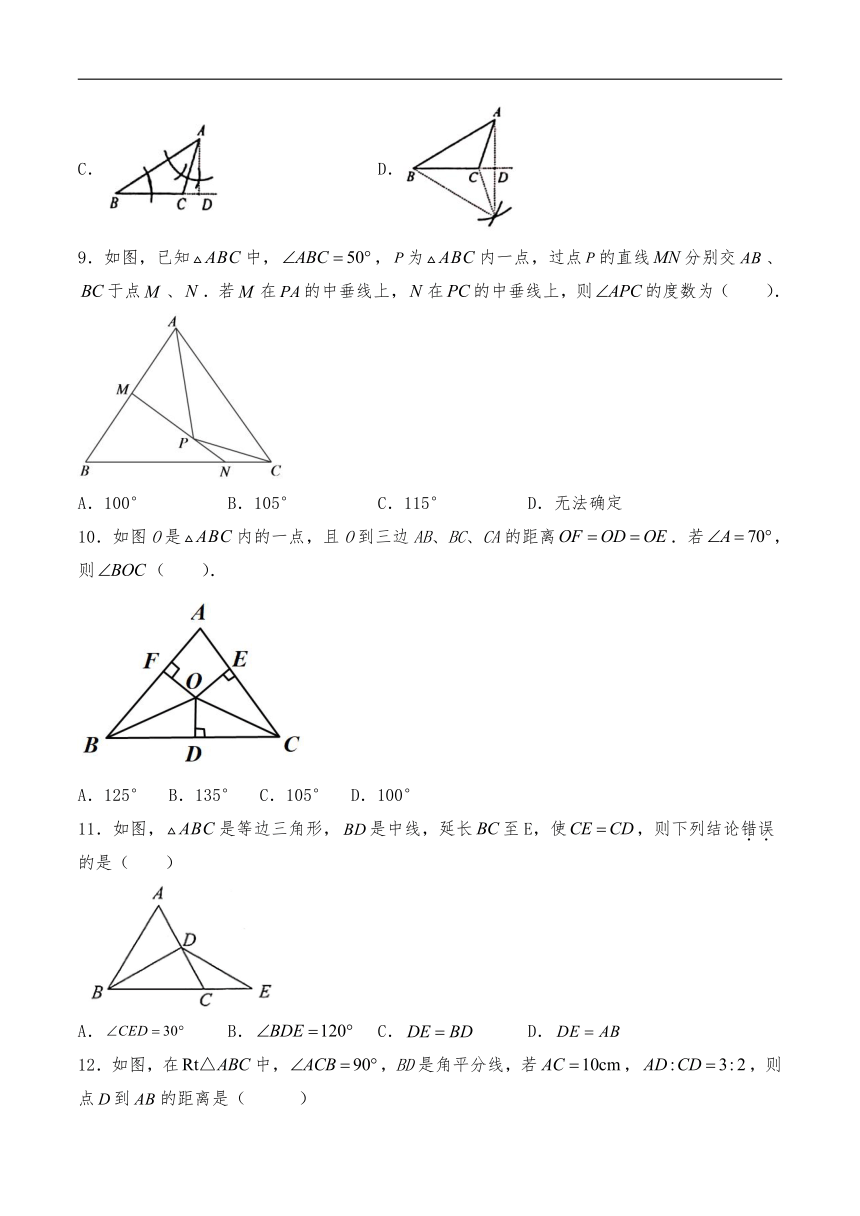


文档简介
第一章 三角形的证明单元测试卷
一、选择题(本大题共14个小题,每题2分,共28分,)
1.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=40°,则∠C的度数为( )
A.20° B.30° C.40° D.50°
2.等腰三角形的周长为,其中一边长为,则该等腰三角形的底边长为( )
A. B. C. D.
3.如图,在中,是的角平分线,,若,则的度数为( )
A. B. C. D.
4.已知中,、、分别是、、的对边,下列条件中不能判断是直角三角形的是( )
A. B.
C. D.
5.如图,用尺规作斜边的垂直平分线,其中,现有以下结论:
①;②;③;④.其中正确的是( )
A.①② B.①②③ C.①③④ D.①④
6.等腰三角形一腰的垂直平分线与另一腰所在直线的夹角是40°,则这一等腰三角形的底角为( )
A.65° B.25° C.50° D.65°或25°
7.如图,在RtABC中,∠BAC=90°,以点A为圆心,以AB长为半径作弧交BC于点D,再分别以点B,D为圆心,以大于的长为半径作弧,两弧交于点P,作射线AP交BC于点E,如果AB=3,AC=4,那么线段AE的长度是( )
A. B. C. D.
8.已知,在中,,且,应用尺规作图中构造边上的高,下列作图中不正确的是( )
A. B.
C. D.
9.如图,已知中,,为内一点,过点的直线分别交、于点、.若在的中垂线上,在的中垂线上,则的度数为( ).
A.100° B.105° C.115° D.无法确定
10.如图O是内的一点,且O到三边AB、BC、CA的距离.若,则( ).
A.125° B.135° C.105° D.100°
11.如图,是等边三角形,是中线,延长至E,使,则下列结论错误的是( )
A. B. C. D.
12.如图,在中,,BD是角平分线,若,,则点到的距离是( )
A.6cm B.5cm C.4cm D.3cm
13.将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
A. B.3 C. D.
14.如图,以△ABC的边AB、AC为边向外作等边△ABD与等边△ACE,连接BE交DC于点F,下列结论:①CD=BE;②FA平分∠DFE;③∠BFC=120°;④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本题共4个小题;每个小题3分,共12分,)
15.如图,在中,,,AD平分交BC于D,于E,若的周长是4cm,则AB的长为_________cm.
16.如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于的长为半径作弧,两弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连结AE,则∠AED的度数是______°
17.如图,为等边三角形,则的度数是_________.
18.如图,已知A(1,3),在坐标轴上找点B,使△AOB为等腰三角形,符合条件的点有____个.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在中,是边上一点,是边的中点,作交的延长线于点.
(1)求证:;
(2)若,求的长.
20.如图所示,在图①和图②的网格中,小正方形的边长均为1.
(1)请在图①中画出端点在格点的线段和,使,,并选择其中的一个说明理由
(2)如图②,是一个格点三角形,这个三角形是直角三角形吗?为什么?
21.如图,在△ABC中,AB边的中垂线PQ与△ABC的外角平分线交于点P,过点P作PD⊥BC于点D,PE⊥AC于点E.
(1)求证:BD=AE;
(2)若BC=6,AC=4.求CE的长度.
22.问题:如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.
(1)如图②,作出点A关于l的对称点A',线段A'B与直线l的交点C的位置即为所求,即在点C处建燃气站,所得路线ACB是最短的.
为了证明点C的位置即为所求,不妨在直线l上另外任取一点C',连接AC'、BC',证明AC+CB<AC'+C'B.请完成这个证明.
(2)如图③,点P为∠MON内的一个定点,在OM上有一点A,ON上有一点B.请你作出点A和点B的位置,使得△PAB的周长最小.(保留作图痕迹,不写作法)在上述条件下,若∠MON=40°,则∠APB= °.
23.如图,点为定角的平分线上的一个定点,,,且与互补,若在绕点旋转的过程中,其两边分别与,相交于,两点.
(1)试判断的形状,并给出证明;
(2)的值是否为定值?若是请求出这个定值,若不是,请说明理由;
(3)四边形的面积是否为定值?请说明理由.
24.(问题提出)(1)如图,与均是顶角为的等腰三角形,、分别是底边,求证:;
(类比延伸)(2)如图,与均为等边三角形,点、、在同一直线上,连接.填空:的度数为______;线段与之间的数量关系为______.
(拓展研究)(3)如图,与均为等腰直角三角形,,点、、在同一直线上,于点,连接.请求出的度数及线段、、之间的数量关系,并说明理由.
25.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
26.如图,在平面直角坐标系中,直线交坐标轴于两点,过:x轴正半轴上一点作直线交轴正半轴于点,且.
(1)求出直线对应的函数表达式;
(2)点是线段上一动点(不与点重合),交于点,连接.判断的形状,并说明理由;
(3)若为直线上的点,为轴上的点,请问:直线上是否存在点,使得是以为直角顶点的等腰直角三角形,若存在,请求出此时点的坐标;若不存在,请说明理由.
答案
一、选择题
D.A.C.A.D.D.A.B.C.A.D.C.D.A
二、填空题
15.4. 16.50. 17.120° 18.8.
三、解答题
19.
(1)证明:是边的中点,
.
又,
.
在与中,
;
(2)解:,
,
又,
.
是边的中点,,
.
.
.
20.
解:(1)如图MN、EF即为所求,
理由:小正方形的边长均为1,
,
(2)是直角三角形,
理由:,,
是直角三角形.
21.
(1)连接PA、PB,
∵CP是∠BCE的平分线,PD⊥BC,PE⊥AC,
∴PD=PE,
在Rt△CDP和Rt△CEP中,
,
∴Rt△CDP≌Rt△CEP(HL)
∴CD=CE,
∵PQ是线段AB的垂直平分线,
∴PA=PB,
在Rt△AEP和Rt△BDP中,
,
∴Rt△AEP≌Rt△BDP(HL),
∴AE=BD;
(2)AC+CE+CD=BD+CD=BC=6,
∴.
22.
证明:(1)如图②,连接,
∵点A,点关于l对称,点C在l上,
∴,
∴,
同理可得:,
∵<,
∴AC+BC<;
(2)如图所示,点A、B即为所求,
由轴对称的性质可得:
故答案为:100°.
23.
(1)证明:如图作于,于.
,
,
,
又,
,
平分,于,于,
,
在和中,
,
,
.
又,,
,
为等边三角形.
(2)的值是定值.
理由:在和中,
,
,
,,
又,
,
.
在中,,
,
3,,
.
(3)四边形是一个定值,
理由:,
,
四边形的面积是一个定值.
24.
(1)证明:∵,
∴,即,
在和中,,
∴,
∴;
(2)∵△ABC和△ADE均是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠ADE=∠AED=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ADB=∠AEC,
∵∠ADE=60°,
∴∠AEC=∠ADB=180°-∠ADE=120°,
故答案为:120°,BE=AD;
(3)解:∵和均为等腰直角三角形,
∴,,,,
∴,即,
在和中,,
∴,
∴,
∵,,,
∴,
∴,
∴;
即线段、、之间的数量关系为:.
25.
解:(1)∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形.
(2)△AOD是直角三角形.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形.
(3)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,
α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
26.
(1)把代入得:
把代入得:,
设直线对应的函数表达式为:
把代入得:,
解得:
直线对应的函数表达式为:
是等腰直角三角形.理由如下:
又
即
即
在与中,
又
是等腰直角三角形
(3)直线上存在点,使得是以为直角顶点的等腰三角形.
在直线上,代入得:
当点在点下方时,如图一所示连接,过点作交的延长线于点
轴且点的纵坐标为
是以为直角顶点的等腰三角形
在与中,
点的纵坐标为
把代入中得:
当点在点上方时,如图二所示点作轴,过点作于点,过点作交的延长线于点.
则
点的橫坐标为,
则
是以为直角顶点的等腰三角形
在与中,
点的纵坐标为
点的纵坐标为
把代入中得:
综上所述,直线上存在点,使得是以为直角顶点的等腰三角形.且或.
一、选择题(本大题共14个小题,每题2分,共28分,)
1.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=40°,则∠C的度数为( )
A.20° B.30° C.40° D.50°
2.等腰三角形的周长为,其中一边长为,则该等腰三角形的底边长为( )
A. B. C. D.
3.如图,在中,是的角平分线,,若,则的度数为( )
A. B. C. D.
4.已知中,、、分别是、、的对边,下列条件中不能判断是直角三角形的是( )
A. B.
C. D.
5.如图,用尺规作斜边的垂直平分线,其中,现有以下结论:
①;②;③;④.其中正确的是( )
A.①② B.①②③ C.①③④ D.①④
6.等腰三角形一腰的垂直平分线与另一腰所在直线的夹角是40°,则这一等腰三角形的底角为( )
A.65° B.25° C.50° D.65°或25°
7.如图,在RtABC中,∠BAC=90°,以点A为圆心,以AB长为半径作弧交BC于点D,再分别以点B,D为圆心,以大于的长为半径作弧,两弧交于点P,作射线AP交BC于点E,如果AB=3,AC=4,那么线段AE的长度是( )
A. B. C. D.
8.已知,在中,,且,应用尺规作图中构造边上的高,下列作图中不正确的是( )
A. B.
C. D.
9.如图,已知中,,为内一点,过点的直线分别交、于点、.若在的中垂线上,在的中垂线上,则的度数为( ).
A.100° B.105° C.115° D.无法确定
10.如图O是内的一点,且O到三边AB、BC、CA的距离.若,则( ).
A.125° B.135° C.105° D.100°
11.如图,是等边三角形,是中线,延长至E,使,则下列结论错误的是( )
A. B. C. D.
12.如图,在中,,BD是角平分线,若,,则点到的距离是( )
A.6cm B.5cm C.4cm D.3cm
13.将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
A. B.3 C. D.
14.如图,以△ABC的边AB、AC为边向外作等边△ABD与等边△ACE,连接BE交DC于点F,下列结论:①CD=BE;②FA平分∠DFE;③∠BFC=120°;④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本题共4个小题;每个小题3分,共12分,)
15.如图,在中,,,AD平分交BC于D,于E,若的周长是4cm,则AB的长为_________cm.
16.如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于的长为半径作弧,两弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连结AE,则∠AED的度数是______°
17.如图,为等边三角形,则的度数是_________.
18.如图,已知A(1,3),在坐标轴上找点B,使△AOB为等腰三角形,符合条件的点有____个.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在中,是边上一点,是边的中点,作交的延长线于点.
(1)求证:;
(2)若,求的长.
20.如图所示,在图①和图②的网格中,小正方形的边长均为1.
(1)请在图①中画出端点在格点的线段和,使,,并选择其中的一个说明理由
(2)如图②,是一个格点三角形,这个三角形是直角三角形吗?为什么?
21.如图,在△ABC中,AB边的中垂线PQ与△ABC的外角平分线交于点P,过点P作PD⊥BC于点D,PE⊥AC于点E.
(1)求证:BD=AE;
(2)若BC=6,AC=4.求CE的长度.
22.问题:如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.
(1)如图②,作出点A关于l的对称点A',线段A'B与直线l的交点C的位置即为所求,即在点C处建燃气站,所得路线ACB是最短的.
为了证明点C的位置即为所求,不妨在直线l上另外任取一点C',连接AC'、BC',证明AC+CB<AC'+C'B.请完成这个证明.
(2)如图③,点P为∠MON内的一个定点,在OM上有一点A,ON上有一点B.请你作出点A和点B的位置,使得△PAB的周长最小.(保留作图痕迹,不写作法)在上述条件下,若∠MON=40°,则∠APB= °.
23.如图,点为定角的平分线上的一个定点,,,且与互补,若在绕点旋转的过程中,其两边分别与,相交于,两点.
(1)试判断的形状,并给出证明;
(2)的值是否为定值?若是请求出这个定值,若不是,请说明理由;
(3)四边形的面积是否为定值?请说明理由.
24.(问题提出)(1)如图,与均是顶角为的等腰三角形,、分别是底边,求证:;
(类比延伸)(2)如图,与均为等边三角形,点、、在同一直线上,连接.填空:的度数为______;线段与之间的数量关系为______.
(拓展研究)(3)如图,与均为等腰直角三角形,,点、、在同一直线上,于点,连接.请求出的度数及线段、、之间的数量关系,并说明理由.
25.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
26.如图,在平面直角坐标系中,直线交坐标轴于两点,过:x轴正半轴上一点作直线交轴正半轴于点,且.
(1)求出直线对应的函数表达式;
(2)点是线段上一动点(不与点重合),交于点,连接.判断的形状,并说明理由;
(3)若为直线上的点,为轴上的点,请问:直线上是否存在点,使得是以为直角顶点的等腰直角三角形,若存在,请求出此时点的坐标;若不存在,请说明理由.
答案
一、选择题
D.A.C.A.D.D.A.B.C.A.D.C.D.A
二、填空题
15.4. 16.50. 17.120° 18.8.
三、解答题
19.
(1)证明:是边的中点,
.
又,
.
在与中,
;
(2)解:,
,
又,
.
是边的中点,,
.
.
.
20.
解:(1)如图MN、EF即为所求,
理由:小正方形的边长均为1,
,
(2)是直角三角形,
理由:,,
是直角三角形.
21.
(1)连接PA、PB,
∵CP是∠BCE的平分线,PD⊥BC,PE⊥AC,
∴PD=PE,
在Rt△CDP和Rt△CEP中,
,
∴Rt△CDP≌Rt△CEP(HL)
∴CD=CE,
∵PQ是线段AB的垂直平分线,
∴PA=PB,
在Rt△AEP和Rt△BDP中,
,
∴Rt△AEP≌Rt△BDP(HL),
∴AE=BD;
(2)AC+CE+CD=BD+CD=BC=6,
∴.
22.
证明:(1)如图②,连接,
∵点A,点关于l对称,点C在l上,
∴,
∴,
同理可得:,
∵<,
∴AC+BC<;
(2)如图所示,点A、B即为所求,
由轴对称的性质可得:
故答案为:100°.
23.
(1)证明:如图作于,于.
,
,
,
又,
,
平分,于,于,
,
在和中,
,
,
.
又,,
,
为等边三角形.
(2)的值是定值.
理由:在和中,
,
,
,,
又,
,
.
在中,,
,
3,,
.
(3)四边形是一个定值,
理由:,
,
四边形的面积是一个定值.
24.
(1)证明:∵,
∴,即,
在和中,,
∴,
∴;
(2)∵△ABC和△ADE均是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠ADE=∠AED=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ADB=∠AEC,
∵∠ADE=60°,
∴∠AEC=∠ADB=180°-∠ADE=120°,
故答案为:120°,BE=AD;
(3)解:∵和均为等腰直角三角形,
∴,,,,
∴,即,
在和中,,
∴,
∴,
∵,,,
∴,
∴,
∴;
即线段、、之间的数量关系为:.
25.
解:(1)∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形.
(2)△AOD是直角三角形.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形.
(3)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,
α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
26.
(1)把代入得:
把代入得:,
设直线对应的函数表达式为:
把代入得:,
解得:
直线对应的函数表达式为:
是等腰直角三角形.理由如下:
又
即
即
在与中,
又
是等腰直角三角形
(3)直线上存在点,使得是以为直角顶点的等腰三角形.
在直线上,代入得:
当点在点下方时,如图一所示连接,过点作交的延长线于点
轴且点的纵坐标为
是以为直角顶点的等腰三角形
在与中,
点的纵坐标为
把代入中得:
当点在点上方时,如图二所示点作轴,过点作于点,过点作交的延长线于点.
则
点的橫坐标为,
则
是以为直角顶点的等腰三角形
在与中,
点的纵坐标为
点的纵坐标为
把代入中得:
综上所述,直线上存在点,使得是以为直角顶点的等腰三角形.且或.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
