认识不等式[上学期]
图片预览

文档简介
认识不等式
一 教材分析
不等式在现实世界中无处不有,如倾斜的天平,年龄的大小,个子的高低,身体的轻重,速度的快慢,路程的远近,怎样设计方案划算等都表现为不等关系.本节是一元一次不等式这章的第一节,它是后面学习不等式的基础.
二 学习分析
学生在学习了一元一次方程,二元一次方程组的基础上才开始研究简单的不等关系,进行不等关系的学习已经是顺理成章,对于不等式,学生能感受到它的存在,但没把它与数学知识联系起来.通过跷跷板的引入及天平实验,使学生能够在具体情景中感受概念.
三 教学目标
1 通过生活中的情境,建立数学模型,抽象为不等关系,让学生在体验中感受不等关系.
2 正确理解不等式及其解的概念.
3 能根据数量关系列不等式,并能根据概念解决一些简单问题.
4 进一步理解从具体到抽象获取知识的思维方式.
四 教学过程
教学环节 教学内容 设计意图
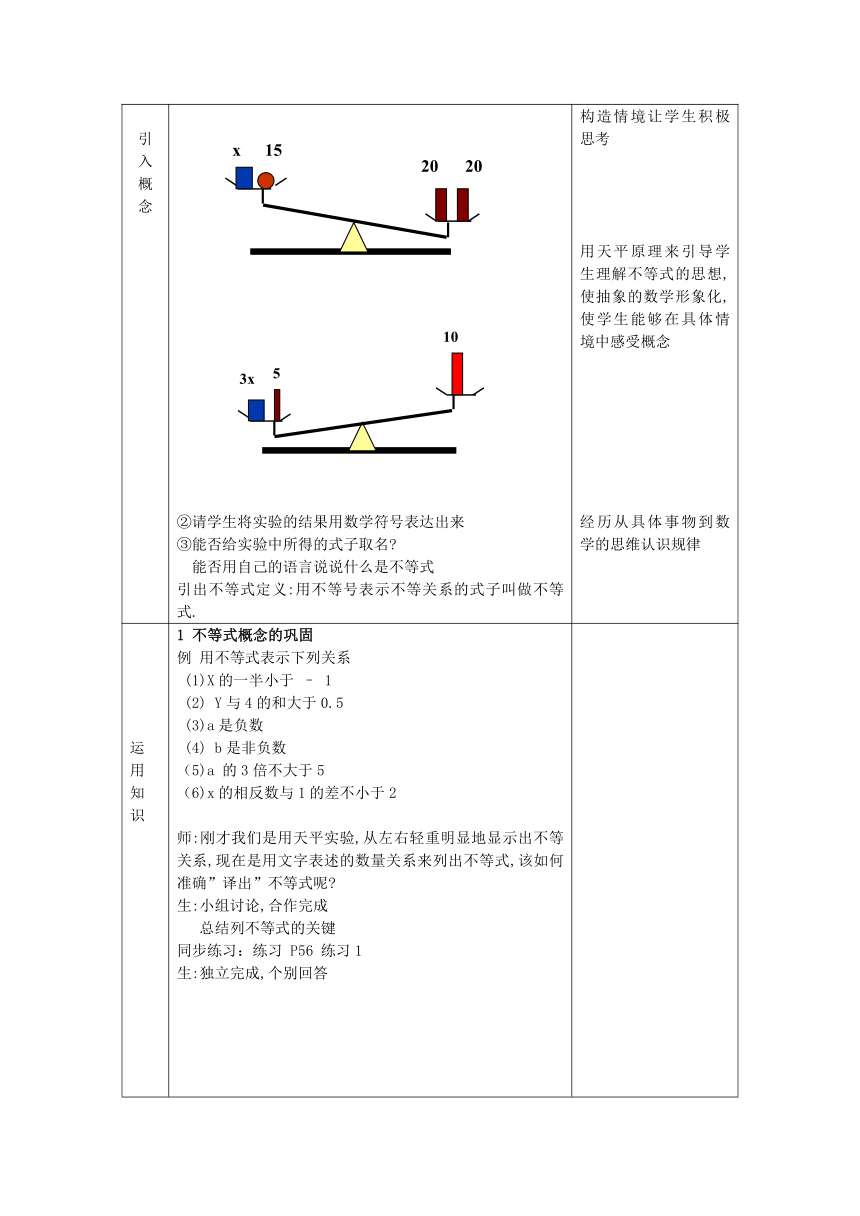
创设情 境,引入概念 显示跷跷板课件,引入课题实验 ①出示一个天平 如图①,图②,图③(多媒体显示) 利用跷跷板作为引入,引起学生的兴趣,有效地改进学生的学习,同时将不等关系自然过渡过来
②请学生将实验的结果用数学符号表达出来③能否给实验中所得的式子取名 能否用自己的语言说说什么是不等式引出不等式定义:用不等号表示不等关系的式子叫做不等式. 构造情境让学生积极思考用天平原理来引导学生理解不等式的思想,使抽象的数学形象化,使学生能够在具体情境中感受概念经历从具体事物到数学的思维认识规律
运用知识巩固知识 1 不等式概念的巩固例 用不等式表示下列关系(1)X的一半小于 – 1 (2) Y与4的和大于0.5(3)a是负数(4) b是非负数(5)a 的3倍不大于5(6)x的相反数与1的差不小于2师:刚才我们是用天平实验,从左右轻重明显地显示出不等关系,现在是用文字表述的数量关系来列出不等式,该如何准确”译出”不等式呢 生:小组讨论,合作完成 总结列不等式的关键同步练习:练习 P56 练习1生:独立完成,个别回答体会生活中数量的不等关系,引入不等式的解的定义在潮州首届旅游文化节中,潮州西湖公园举办花灯展,为了加强同学们对潮州传统文化的了解,丰富同学们的学习生活,班委组织同学前往参观,共有27名同学参加了这次活动.西湖公园的门票是:每人5元,一次购票满30张,每票可少1元.假如你是购票者,你会怎样买票 ①你准备买30张还是27张 ②是否要多买票一定花钱少呢 如果是21人去还买30张票吗 ③那么,至少要多少人去,多买票反而少花钱呢 人数X按实际人数购票的付款 5X买团体付款与实际付款比较比较120与5X大小 买团体票合算吗 120﹤5x成立吗 21102120>5x不成立22110120>5x不成立23115120>5x不成立24120120=5x不成立25125120﹤5x成立26130120﹤5x成立27135120﹤5x成立28140120﹤5x成立29145120﹤5x成立④少于30人时,至少要有 人进公园,买30张票反而合算. 公园推出优惠活动目的是吸引顾客,这是一种促销手段,而我们应善于用数学的眼光去选择最适合自己的方案⑤ 由上表引入不等式的解的概念定义:使不等式成立的未知数的值叫做不等式的解⑥ 同步练习 下列各数: ,0 , -1,,1.5,2。其中使不等式X+1>2 成立的是 练习 P56返回例1用不等式表示下列关系 写出两个满足各不等式的数(1)X的一半小于 – 1 (2) Y与4的和大于0.5(3)a是负数(4) b是非负数(5)a 的3倍不大于5(6)x的相反数与1的差不小于23 学生举例体会生活中的不等关系的现象 教学设计中由浅到深的问题,由具体到抽象的概括,体现了由感性到理性的思维过程,并渗透了”教师是主导,学生是主体”的教学理念使学生体会到现实世界中大量存在不等关系,比较数量大小,研究它们的变化规律,是人们在工作和生活只能感解决实际问题的需要从具体事例进一步加深学生对不等式的理解.通过练习加深对不等式的解的认识
小结 学习了这节课有何收获 不等式的概念②不等式的解③利用不等式解决实际问题
作业 必作题:P56 习题 13.1 2 .3 思考题:某人新买一部手机欲入网使用,若入“全球通”电信网,使用的收费标准为每分钟0.2元,另月收18元租费,若入“神州行”联通网,使用的收费标准为每分钟0.3元,不再收月租。有人建议他入“全球通”电信网,也有人建议他入“神州行”联通网,你认为他应该选择哪个网比较划算呢?请你说明理由。课后活动题:请你调查电信收费情况,为你的家人或是你的朋友设计一个用于电信支出最划算的方案
x
20 20
15
8
x
2000
10
5
3x
一 教材分析
不等式在现实世界中无处不有,如倾斜的天平,年龄的大小,个子的高低,身体的轻重,速度的快慢,路程的远近,怎样设计方案划算等都表现为不等关系.本节是一元一次不等式这章的第一节,它是后面学习不等式的基础.
二 学习分析
学生在学习了一元一次方程,二元一次方程组的基础上才开始研究简单的不等关系,进行不等关系的学习已经是顺理成章,对于不等式,学生能感受到它的存在,但没把它与数学知识联系起来.通过跷跷板的引入及天平实验,使学生能够在具体情景中感受概念.
三 教学目标
1 通过生活中的情境,建立数学模型,抽象为不等关系,让学生在体验中感受不等关系.
2 正确理解不等式及其解的概念.
3 能根据数量关系列不等式,并能根据概念解决一些简单问题.
4 进一步理解从具体到抽象获取知识的思维方式.
四 教学过程
教学环节 教学内容 设计意图
创设情 境,引入概念 显示跷跷板课件,引入课题实验 ①出示一个天平 如图①,图②,图③(多媒体显示) 利用跷跷板作为引入,引起学生的兴趣,有效地改进学生的学习,同时将不等关系自然过渡过来
②请学生将实验的结果用数学符号表达出来③能否给实验中所得的式子取名 能否用自己的语言说说什么是不等式引出不等式定义:用不等号表示不等关系的式子叫做不等式. 构造情境让学生积极思考用天平原理来引导学生理解不等式的思想,使抽象的数学形象化,使学生能够在具体情境中感受概念经历从具体事物到数学的思维认识规律
运用知识巩固知识 1 不等式概念的巩固例 用不等式表示下列关系(1)X的一半小于 – 1 (2) Y与4的和大于0.5(3)a是负数(4) b是非负数(5)a 的3倍不大于5(6)x的相反数与1的差不小于2师:刚才我们是用天平实验,从左右轻重明显地显示出不等关系,现在是用文字表述的数量关系来列出不等式,该如何准确”译出”不等式呢 生:小组讨论,合作完成 总结列不等式的关键同步练习:练习 P56 练习1生:独立完成,个别回答体会生活中数量的不等关系,引入不等式的解的定义在潮州首届旅游文化节中,潮州西湖公园举办花灯展,为了加强同学们对潮州传统文化的了解,丰富同学们的学习生活,班委组织同学前往参观,共有27名同学参加了这次活动.西湖公园的门票是:每人5元,一次购票满30张,每票可少1元.假如你是购票者,你会怎样买票 ①你准备买30张还是27张 ②是否要多买票一定花钱少呢 如果是21人去还买30张票吗 ③那么,至少要多少人去,多买票反而少花钱呢 人数X按实际人数购票的付款 5X买团体付款与实际付款比较比较120与5X大小 买团体票合算吗 120﹤5x成立吗 21102120>5x不成立22110120>5x不成立23115120>5x不成立24120120=5x不成立25125120﹤5x成立26130120﹤5x成立27135120﹤5x成立28140120﹤5x成立29145120﹤5x成立④少于30人时,至少要有 人进公园,买30张票反而合算. 公园推出优惠活动目的是吸引顾客,这是一种促销手段,而我们应善于用数学的眼光去选择最适合自己的方案⑤ 由上表引入不等式的解的概念定义:使不等式成立的未知数的值叫做不等式的解⑥ 同步练习 下列各数: ,0 , -1,,1.5,2。其中使不等式X+1>2 成立的是 练习 P56返回例1用不等式表示下列关系 写出两个满足各不等式的数(1)X的一半小于 – 1 (2) Y与4的和大于0.5(3)a是负数(4) b是非负数(5)a 的3倍不大于5(6)x的相反数与1的差不小于23 学生举例体会生活中的不等关系的现象 教学设计中由浅到深的问题,由具体到抽象的概括,体现了由感性到理性的思维过程,并渗透了”教师是主导,学生是主体”的教学理念使学生体会到现实世界中大量存在不等关系,比较数量大小,研究它们的变化规律,是人们在工作和生活只能感解决实际问题的需要从具体事例进一步加深学生对不等式的理解.通过练习加深对不等式的解的认识
小结 学习了这节课有何收获 不等式的概念②不等式的解③利用不等式解决实际问题
作业 必作题:P56 习题 13.1 2 .3 思考题:某人新买一部手机欲入网使用,若入“全球通”电信网,使用的收费标准为每分钟0.2元,另月收18元租费,若入“神州行”联通网,使用的收费标准为每分钟0.3元,不再收月租。有人建议他入“全球通”电信网,也有人建议他入“神州行”联通网,你认为他应该选择哪个网比较划算呢?请你说明理由。课后活动题:请你调查电信收费情况,为你的家人或是你的朋友设计一个用于电信支出最划算的方案
x
20 20
15
8
x
2000
10
5
3x
